Классификация Используя самых близких соседей

Попарные метрики расстояния

Категоризация точек запроса на основе их расстояния до точек в обучающем наборе данных может быть простым все же эффективным способом классифицировать новые точки. Можно использовать различные метрики, чтобы определить расстояние, описанное затем. Использование pdist2 найти расстояние между набором данных и точками запроса.

Метрики расстояния

Учитывая mx-by-n матрица данных X, который обработан как mx (1 n) векторы-строки _x1, _x2..., _xmx и my-by-n матрица данных Y, который обработан как my (1 n) векторы-строки _y1, _y2..., _ymy, определяются следующим образом различные расстояния между векторным _xs и _yt:

Евклидово расстояние
$d_{s t}^{2} = (x_{s} - y_{t}) (x_{s} - y_{t})^{'} .$
Евклидово расстояние является особым случаем расстояния Минковскего, где p = 2.
Стандартизированное Евклидово расстояние
$d_{s t}^{2} = (x_{s} - y_{t}) V^{- 1} (x_{s} - y_{t})^{'},$
где V является n-by-n диагональная матрица, j которой th диагональный элемент (S (j))², где S является вектором из масштабных коэффициентов для каждой размерности.
Расстояние Mahalanobis
$d_{s t}^{2} = (x_{s} - y_{t}) C^{- 1} (x_{s} - y_{t})^{'},$
где C является ковариационной матрицей.
Расстояние городского квартала
$d_{s t} = \sum_{j = 1}^{n} | x_{s j} - y_{t j} | .$
Расстояние городского квартала является особым случаем расстояния Минковскего, где p = 1.
Расстояние Минковскего
$d_{s t} = \sqrt[p]{\sum_{j = 1}^{n} {| x_{s j} - y_{t j} |}^{p}} .$
Для особого случая p = 1, расстояние Минковскего дает расстояние городского квартала. Для особого случая p = 2, расстояние Минковскего дает Евклидово расстояние. Для особого случая p = ∞, расстояние Минковскего дает расстояние Чебычева.
Расстояние Чебычева
$d_{s t} = \max_{j} {| x_{s j} - y_{t j} |} .$
Расстояние Чебычева является особым случаем расстояния Минковскего, где p = ∞.
Расстояние косинуса
$d_{s t} = (1 - \frac{x_{s} {y^{'}}_{t}}{\sqrt{(x_{s} {x^{'}}_{s}) (y_{t} {y^{'}}_{t})}}) .$
Расстояние корреляции
$d_{s t} = 1 - \frac{(x_{s} - {\bar{x}}_{s}) {(y_{t} - {\bar{y}}_{t})}^{'}}{\sqrt{(x_{s} - {\bar{x}}_{s}) {(x_{s} - {\bar{x}}_{s})}^{'}} \sqrt{(y_{t} - {\bar{y}}_{t}) {(y_{t} - {\bar{y}}_{t})}^{'}}},$
где
${\bar{x}}_{s} = \frac{1}{n} \sum_{j} x_{s j}$
и
${\bar{y}}_{t} = \frac{1}{n} \sum_{j} y_{t j} .$
Расстояние Хемминга
$d_{s t} = (# (x_{s j} \neq y_{t j}) / n) .$
Расстояние Jaccard
$d_{s t} = \frac{# [(x_{s j} \neq y_{t j}) \cap ((x_{s j} \neq 0) \cup (y_{t j} \neq 0))]}{# [(x_{s j} \neq 0) \cup (y_{t j} \neq 0)]} .$
Расстояние копьеносца
$d_{s t} = 1 - \frac{(r_{s} - {\bar{r}}_{s}) {(r_{t} - {\bar{r}}_{t})}^{'}}{\sqrt{(r_{s} - {\bar{r}}_{s}) {(r_{s} - {\bar{r}}_{s})}^{'}} \sqrt{(r_{t} - {\bar{r}}_{t}) {(r_{t} - {\bar{r}}_{t})}^{'}}},$
где
- _rsj является рангом _xsj, принятого x _1j, x _2j... _xmx,j, как вычислено tiedrank.
- _rtj является рангом _ytj, принятого y _1j, y _2j... _ymy,j, как вычислено tiedrank.
- _rs и _rt являются координатно-мудрыми векторами ранга из _xs и _yt, то есть, _rs = (_rs ₁, _rs ₂... _rsn) и _rt = (r _{t 1}, r _{t 2}... _rtn).
- ${\bar{r}}_{s} = \frac{1}{n} \sum_{j} r_{s j} = \frac{(n + 1)}{2}$ .
- ${\bar{r}}_{t} = \frac{1}{n} \sum_{j} r_{t j} = \frac{(n + 1)}{2}$ .

k- соседний поиск поиска и радиуса

Учитывая набор X точек n и функции расстояния, k - самый близкий сосед (k NN) поиск позволяет вам найти k самыми близкими точками в X к точке запроса или набору точек Y. Метод поиска NN k и k основанные на NN алгоритмы широко используются в качестве правил изучения сравнительного теста. Относительная простота метода поиска NN k дает возможность сравнивать результаты других методов классификации с k результаты NN. Метод использовался в различных областях, таких как:

биоинформатика
обработка изображений и сжатие данных
поиск документов
компьютерное зрение
мультимедийная база данных
маркетинг анализа данных

Можно использовать k, как который NN ищут другие алгоритмы машинного обучения, такие:

k классификация NN
локальная взвешенная регрессия
недостающее обвинение данных и интерполяция
оценка плотности

Можно также использовать k поиск NN со многими основанными на расстоянии функциями изучения, такими как кластеризация K-средних значений.

В отличие от этого для положительного вещественного значения r, rangesearch находит все точки в X это - на расстоянии r из каждой точки в Y. Этот поиск фиксированного радиуса тесно связан с k поиск NN, когда это поддерживает те же метрики расстояния и поисковые классы, и использует те же алгоритмы поиска.

k- соседний поиск Используя исчерпывающий поиск

Когда ваши входные данные соответствуют любому из следующих критериев, knnsearch использует метод исчерпывающего поиска по умолчанию, чтобы найти k - самые близкие соседи:

Количество столбцов X больше чем 10.
X issparse .
Метрика расстояния также:
- 'seuclidean'
- 'mahalanobis'
- 'cosine'
- 'correlation'
- 'spearman'
- 'hamming'
- 'jaccard'
- Пользовательская функция расстояния

knnsearch также использует метод исчерпывающего поиска, если вашим поисковым объектом является ExhaustiveSearcher объект модели. Метод исчерпывающего поиска находит расстояние от каждой точки запроса до каждой точки в X, оценивает их в порядке возрастания и возвращает точки k с наименьшими расстояниями. Например, эта схема показывает k = 3 самых близких соседа.

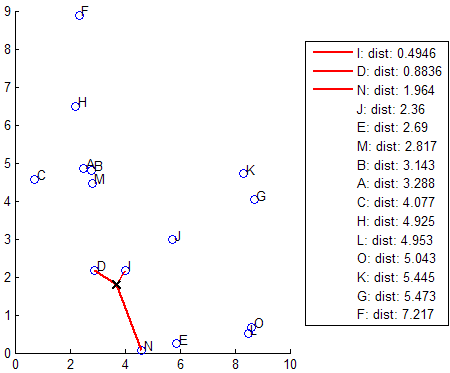
k- соседний поиск Используя d-дерево K

Когда ваши входные данные соответствуют всем следующим критериям, knnsearch создает d-дерево K по умолчанию, чтобы найти k - самые близкие соседи:

Количество столбцов X меньше 10.
X не разреженно.
Метрика расстояния также:
- 'euclidean' (значение по умолчанию)
- 'cityblock'
- 'minkowski'
- 'chebychev'

knnsearch также использует d-дерево K, если вашим поисковым объектом является KDTreeSearcher объект модели.

D-деревья K делят ваши данные на узлы с в большей части BucketSize (значение по умолчанию равняется 50), точки на узел, на основе координат (в противоположность категориям). Следующие схемы иллюстрируют эту концепцию с помощью patch объекты к цветовому коду различные “блоки”.

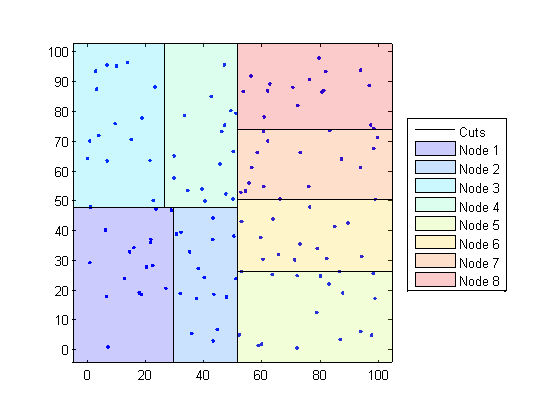
Когда это необходимо, найти k - самые близкие соседи данной точки запроса, knnsearch делает следующее:

Определяет узел, которому принадлежит точка запроса. В следующем примере точка запроса (32,90) принадлежит Узлу 4.
Находит самые близкие точки k в том узле и его расстоянии до точки запроса. В следующем примере точки в красных кругах являются равноотстоящими от точки запроса и являются самыми близкими точками к точке запроса в Узле 4.
Выбирает все другие узлы, имеющие любую область, которая является на том же расстоянии, в любом направлении, от точки запроса до k th самая близкая точка. В этом примере, только Узел 3 перекрытия чистый черный круг, сосредоточенный в точке запроса с радиусом, равняются расстоянию до самых близких точек в Узле 4.
Узлы поисковых запросов в той области значений для любых точек ближе к точке запроса. В следующем примере точка в красном квадрате немного ближе к точке запроса, чем те в Узле 4.

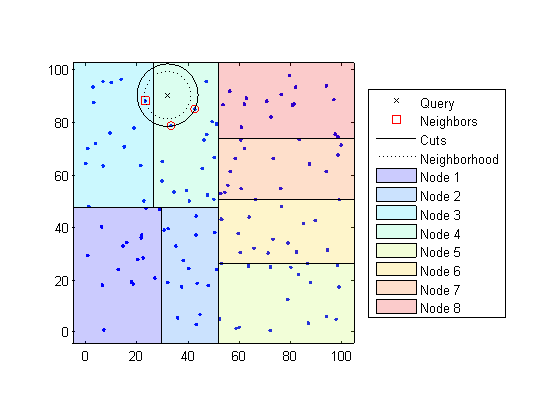
Используя d-дерево K для больших наборов данных меньше чем с 10 размерностями (столбцы) может быть намного более эффективным, чем использование метода исчерпывающего поиска, как knnsearch потребности вычислить только подмножество расстояний. Чтобы максимизировать КПД d-деревьев K, используйте KDTreeSearcher модель.

Что такое поисковые объекты модели?

В основном объекты модели являются удобным способом хранить информацию. Связанные модели имеют те же свойства со значениями, и вводит относящийся к заданному методу поиска. В дополнение к тому, чтобы хранить информацию в моделях можно выполнить определенные действия на моделях.

Можно эффективно выполнить k - самые близкие соседи ищут на поисковом использовании модели knnsearch. Или, можно искать всех соседей в заданном радиусе с помощью поисковой модели и rangesearch. Кроме того, существует дженерик knnsearch и rangesearch функции, которые ищут, не создавая или с помощью модели.

Чтобы определить, какой тип и метода поиска модели является лучшим для ваших данных, рассмотрите следующее:

Ваши данные имеют много столбцов, говорят больше чем 10? ExhaustiveSearcher модель может выполнить лучше.
Действительно ли ваши данные разреженны? Используйте ExhaustiveSearcher модель.
Вы хотите использовать одну из этих метрик расстояния, чтобы найти самых близких соседей? Используйте ExhaustiveSearcher модель.
- 'seuclidean'
- 'mahalanobis'
- 'cosine'
- 'correlation'
- 'spearman'
- 'hamming'
- 'jaccard'
- Пользовательская функция расстояния
Действительно ли ваш набор данных огромен (но меньше чем с 10 столбцами)? Используйте KDTreeSearcher модель.
Вы ищете самых близких соседей к большому количеству точек запроса? Используйте KDTreeSearcher модель.

Классифицируйте данные о запросе

Скрипт Open Live Script

В этом примере показано, как классифицировать данные о запросе:

Рост Kd-дерева
Проведение k самого близкого соседнего поиска с помощью выращенного дерева.
Присвоение каждой точки запроса класс с самым высоким представлением среди их соответствующих самых близких соседей.

Классифицируйте новую точку на основе последних двух столбцов ирисовых данных Фишера. Только Используя последние два столбца облегчает строить.

load fisheriris
x = meas(:,3:4);
gscatter(x(:,1),x(:,2),species)
legend('Location','best')

Figure contains an axes object. The axes object contains 3 objects of type line. These objects represent setosa, versicolor, virginica.

Постройте новую точку.

newpoint = [5 1.45];
line(newpoint(1),newpoint(2),'marker','x','color','k',...
   'markersize',10,'linewidth',2)

Figure contains an axes object. The axes object contains 4 objects of type line. These objects represent setosa, versicolor, virginica.

Подготовьтесь Kd-дерево граничат с моделью искателя.

Mdl = KDTreeSearcher(x)

Mdl = 
  KDTreeSearcher with properties:

       BucketSize: 50
         Distance: 'euclidean'
    DistParameter: []
                X: [150x2 double]

Mdl KDTreeSearcher модель. По умолчанию метрика расстояния, которую это использует, чтобы искать соседей, является Евклидовым расстоянием.

Найдите 10 точек выборки самыми близкими к новой точке.

[n,d] = knnsearch(Mdl,newpoint,'k',10);
line(x(n,1),x(n,2),'color',[.5 .5 .5],'marker','o',...
    'linestyle','none','markersize',10)

Figure contains an axes object. The axes object contains 5 objects of type line. These objects represent setosa, versicolor, virginica.

Это появляется тот knnsearch нашел только самые близкие восемь соседей. На самом деле этот конкретный набор данных содержит дублирующиеся значения.

x(n,:)

ans = 10×2

    5.0000    1.5000
    4.9000    1.5000
    4.9000    1.5000
    5.1000    1.5000
    5.1000    1.6000
    4.8000    1.4000
    5.0000    1.7000
    4.7000    1.4000
    4.7000    1.4000
    4.7000    1.5000

Сделайте оси равными, таким образом, расчетные расстояния соответствуют очевидным расстояниям на равной оси графика и увеличение, чтобы видеть соседей лучше.

xlim([4.5 5.5]);
ylim([1 2]);
axis square

Figure contains an axes object. The axes object contains 5 objects of type line. These objects represent setosa, versicolor, virginica.

Найдите разновидности 10 соседей.

tabulate(species(n))

       Value    Count   Percent
   virginica        2     20.00%
  versicolor        8     80.00%

Используя правило на основе решения большинством голосов 10 самых близких соседей, можно классифицировать эту новую точку как versicolor.

Визуально идентифицируйте соседей путем рисования круга вокруг группы их. Задайте центр и диаметр круга, на основе местоположения новой точки.

ctr = newpoint - d(end);
diameter = 2*d(end);
% Draw a circle around the 10 nearest neighbors.
h = rectangle('position',[ctr,diameter,diameter],...
   'curvature',[1 1]);
h.LineStyle = ':';

Figure contains an axes object. The axes object contains 6 objects of type line, rectangle. These objects represent setosa, versicolor, virginica.

Используя тот же набор данных, найдите 10 самых близких соседей трех новых точек.

figure 
newpoint2 = [5 1.45;6 2;2.75 .75];
gscatter(x(:,1),x(:,2),species)
legend('location','best')
[n2,d2] = knnsearch(Mdl,newpoint2,'k',10);
line(x(n2,1),x(n2,2),'color',[.5 .5 .5],'marker','o',...
   'linestyle','none','markersize',10)
line(newpoint2(:,1),newpoint2(:,2),'marker','x','color','k',...
   'markersize',10,'linewidth',2,'linestyle','none')

Figure contains an axes object. The axes object contains 5 objects of type line. These objects represent setosa, versicolor, virginica.

Найдите разновидности 10 самых близких соседей к каждой новой точке.

tabulate(species(n2(1,:)))

       Value    Count   Percent
   virginica        2     20.00%
  versicolor        8     80.00%

tabulate(species(n2(2,:)))

      Value    Count   Percent
  virginica       10    100.00%

tabulate(species(n2(3,:)))

       Value    Count   Percent
  versicolor        7     70.00%
      setosa        3     30.00%

Для большего количества примеров с помощью knnsearch методы и функция, смотрите отдельные страницы с описанием.

Найдите самых близких соседей Используя пользовательскую метрику расстояния

Скрипт Open Live Script

В этом примере показано, как найти индексы трех самых близких наблюдений в X к каждому наблюдению в Y относительно расстояния хи-квадрата. Эта метрика расстояния используется в анализе соответствия, особенно в экологических приложениях.

Случайным образом сгенерируйте нормально распределенные данные в две матрицы. Количество строк может варьироваться, но количество столбцов должно быть равным. Этот пример использует 2D данные для графического вывода.

rng(1) % For reproducibility
X = randn(50,2);
Y = randn(4,2);

h = zeros(3,1);
figure
h(1) = plot(X(:,1),X(:,2),'bx');
hold on
h(2) = plot(Y(:,1),Y(:,2),'rs','MarkerSize',10);
title('Heterogeneous Data')

Figure contains an axes object. The axes object with title Heterogeneous Data contains 2 objects of type line.

Строки X и Y соответствуйте наблюдениям, и столбцы являются, в целом, размерностями (например, предикторы).

Расстояние хи-квадрата между j-dimensional точками x и z

$χ (x, z) = \sqrt{\sum_{j = 1}^{J} w_{j} {(x_{j} - z_{j})}^{2}},$

где $w_{j}$ вес, сопоставленный с размерностью j.

Выберите веса для каждой размерности и задайте функцию расстояния хи-квадрата. Функция расстояния должна:

Возьмите в качестве входных параметров одну строку X, например, x, и матричный Z.
Сравните x к каждой строке Z.
Возвратите векторный D из длины $n_{z}$ , где $n_{z}$ количество строк Z. Каждый элемент D расстояние между наблюдением, соответствующим x и наблюдения, соответствующие каждой строке Z.

w = [0.4; 0.6];
chiSqrDist = @(x,Z)sqrt((bsxfun(@minus,x,Z).^2)*w);

Этот пример использует произвольные веса для рисунка.

Найдите индексы трех самых близких наблюдений в X к каждому наблюдению в Y.

k = 3;
[Idx,D] = knnsearch(X,Y,'Distance',chiSqrDist,'k',k);

idx и D 4 3 матрицы.

idx(j,1) индекс строки самого близкого наблюдения в X к наблюдению j Y, и D(j,1) их расстояние.
idx(j,2) индекс строки следующего ближайшего наблюдения в X к наблюдению j Y, и D(j,2) их расстояние.
И так далее.

Идентифицируйте самые близкие наблюдения в графике.

for j = 1:k
    h(3) = plot(X(Idx(:,j),1),X(Idx(:,j),2),'ko','MarkerSize',10);
end 
legend(h,{'\texttt{X}','\texttt{Y}','Nearest Neighbor'},'Interpreter','latex')
title('Heterogeneous Data and Nearest Neighbors')
hold off

$Figure contains an axes object. The axes object with title Heterogeneous Data and Nearest Neighbors contains 5 objects of type line. These objects represent \texttt{X}, \texttt{Y}, Nearest Neighbor.$

Несколько наблюдений за Y совместно используйте самых близких соседей.

Проверьте, что метрика расстояния хи-квадрата эквивалентна Евклидовой метрике расстояния, но с дополнительным масштабным коэффициентом.

[IdxE,DE] = knnsearch(X,Y,'Distance','seuclidean','k',k, ...
    'Scale',1./(sqrt(w)));
AreDiffIdx = sum(sum(Idx ~= IdxE))

AreDiffIdx = 0

AreDiffDist = sum(sum(abs(D - DE) > eps))

AreDiffDist = 0

Индексы и расстояния между двумя реализациями трех самых близких соседей практически эквивалентны.

Классификация k - ближайших соседей для контролируемого изучения

ClassificationKNN модель классификации позволяет вам:

Подготовьте свои данные к классификации согласно процедуре на Шагах в Контролируемом Изучении. Затем создайте использование классификатора fitcknn.

Создайте классификатор KNN

Скрипт Open Live Script

В этом примере показано, как создать классификатор k - ближайших соседей для ирисовых данных Фишера.

Загрузите ирисовые данные Фишера.

load fisheriris
X = meas;    % Use all data for fitting
Y = species; % Response data

Создайте классификатор с помощью fitcknn.

Mdl = fitcknn(X,Y)

Mdl = 
  ClassificationKNN
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'setosa'  'versicolor'  'virginica'}
           ScoreTransform: 'none'
          NumObservations: 150
                 Distance: 'euclidean'
             NumNeighbors: 1


  Properties, Methods

Классификатор k - ближайших соседей по умолчанию использует одного самого близкого соседа только. Часто, классификатор более устойчив с большим количеством соседей, чем это.

Измените размер окружения Mdl к 4, значение, что Mdl классифицирует использование четырех самых близких соседей.

Mdl.NumNeighbors = 4;

Исследуйте качество классификатора KNN

Скрипт Open Live Script

В этом примере показано, как исследовать качество классификатора k - ближайших соседей с помощью перезамены и перекрестной проверки.

Создайте классификатор KNN для ирисовых данных Фишера как в Построении Классификатор KNN.

load fisheriris
X = meas;    
Y = species; 
rng(10); % For reproducibility
Mdl = fitcknn(X,Y,'NumNeighbors',4);

Исследуйте потерю перезамены, которая, по умолчанию, является частью misclassifications из предсказаний Mdl. (Для стоимости не по умолчанию веса или уголовное прошлое, видят loss.).

rloss = resubLoss(Mdl)

rloss = 0.0400

Классификатор предсказывает неправильно для 4% обучающих данных.

Создайте перекрестный подтвержденный классификатор из модели.

CVMdl = crossval(Mdl);

Исследуйте потерю перекрестной проверки, которая является средней потерей каждой модели перекрестной проверки при предсказании на данных, которые не используются для обучения.

kloss = kfoldLoss(CVMdl)

kloss = 0.0333

Перекрестная подтвержденная точность классификации напоминает точность перезамены. Поэтому можно ожидать Mdl неправильно классифицировать приблизительно 4% новых данных, принимая, что новые данные имеют о том же распределении как обучающие данные.

Предскажите классификацию Используя классификатор KNN

Скрипт Open Live Script

В этом примере показано, как предсказать классификацию для классификатора k - ближайших соседей.

Создайте классификатор KNN для ирисовых данных Фишера как в Построении Классификатор KNN.

load fisheriris
X = meas;    
Y = species; 
Mdl = fitcknn(X,Y,'NumNeighbors',4);

Предскажите классификацию среднего цветка.

flwr = mean(X); % an average flower
flwrClass = predict(Mdl,flwr)

flwrClass = 1x1 cell array
    {'versicolor'}

Измените классификатор KNN

Скрипт Open Live Script

В этом примере показано, как изменить классификатор k - ближайших соседей.

Создайте классификатор KNN для ирисовых данных Фишера как в Построении Классификатор KNN.

load fisheriris
X = meas;    
Y = species; 
Mdl = fitcknn(X,Y,'NumNeighbors',4);

Измените модель, чтобы использовать трех самых близких соседей, а не значение по умолчанию один самый близкий сосед.

Mdl.NumNeighbors = 3;

Сравните предсказания перезамены и потерю перекрестной проверки с новым количеством соседей.

loss = resubLoss(Mdl)

loss = 0.0400

rng(10); % For reproducibility
CVMdl = crossval(Mdl,'KFold',5);
kloss = kfoldLoss(CVMdl)

kloss = 0.0333

В этом случае модель с тремя соседями имеет ту же перекрестную подтвержденную потерю как модель с четырьмя соседями (см., Исследуют Качество Классификатора KNN).

Измените модель, чтобы использовать расстояние косинуса вместо значения по умолчанию и исследовать потерю. Чтобы использовать расстояние косинуса, необходимо воссоздать модель с помощью метода исчерпывающего поиска.

CMdl = fitcknn(X,Y,'NSMethod','exhaustive','Distance','cosine');
CMdl.NumNeighbors = 3;
closs = resubLoss(CMdl)

closs = 0.0200

Классификатор теперь имеет более низкую ошибку перезамены, чем прежде.

Проверяйте качество перекрестной подтвержденной версии новой модели.

CVCMdl = crossval(CMdl);
kcloss = kfoldLoss(CVCMdl)

kcloss = 0.0200

CVCMdl имеет лучшую перекрестную подтвержденную потерю, чем CVMdl. Однако в целом улучшение ошибки перезамены не обязательно производит модель с лучшими демонстрационными тестом предсказаниями.

Документация