Свойство Matrix объекта преобразования применяет преобразование к дочерним элементам всего объекта в унисон. Преобразования включают вращение, перевод и масштабирование. Задайте преобразование с четырьмя четырьмя матрицей преобразования.
Функция makehgtform упрощает конструкцию матриц, чтобы выполнить вращение, перевод и масштабирование. Для получения информации о создании матриц преобразования с помощью makehgtform смотрите Преобразования Вложенного множества для Комплексных Перемещений.
Преобразования вращения следуют, правило правой руки — вращают объекты о x-, y-, или ось z, с положительными углами, вращающими против часовой стрелки, при наблюдении вдоль соответствующей оси к источнику. Если угол вращения является тетой, следующая матрица задает вращение теты об оси X.
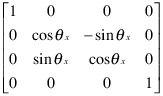
Чтобы создать матрицу преобразования для вращения вокруг произвольной оси, используйте функцию makehgtform.
Перевод преобразовывает объекты перемещения относительно их текущих местоположений. Задайте перевод как расстояния tx, ty, и tz в модулях пространства данных. Следующая матрица показывает местоположение этих элементов в матрице преобразования.

Преобразования масштабирования изменяют размеры объектов. Задайте масштабные коэффициенты sx, sy, и sz и создайте следующую матрицу.
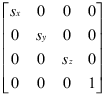
Вы не можете использовать масштабные коэффициенты, меньше чем или равные нулю.
Преобразование по умолчанию является единичной матрицей, которую можно создать с функцией eye. Вот единичная матрица.

Смотрите операции преобразования отмены.
Перспективные преобразования изменяют расстояние, на котором вы просматриваете объект. Следующая матрица является примером перспективной матрицы преобразования, которую не позволяет графика MATLAB®.

В этом случае py является перспективным фактором.
Преобразования сдвига сохраняют все точки вдоль данной строки (или плоскость в 3-D координатах) зафиксированный при сдвиге всех других точек, параллельных строке (плоскость), пропорциональная их перпендикулярному расстоянию от фиксированной строки (плоскость). Следующая матрица является примером матрицы преобразования сдвига, которую не позволяет hgtransform.

В этом случае sx является фактором сдвига и может заменить любой нулевой элемент в единичной матрице.
Преобразования заданы в свободных членах, не относительно текущего преобразования. Например, если вы применяете преобразование, которое переводит объект преобразования 5 модулей в направлении X, и затем вы применяете другое преобразование, которое переводит его 4 модуля в направлении Y, получившееся положение объекта является 4 модулями в направлении Y от его исходного положения.
Если вы хотите, чтобы преобразования накопились, необходимо конкатенировать отдельные преобразования в единственную матрицу. Смотрите Объединяющиеся Преобразования в Одну Матрицу.
Обычно более эффективно объединить различные операции преобразования в одну матрицу путем конкатенации (умножение) отдельных матриц и установка свойства Matrix к результату. Умножение матриц не является коммутативным, таким образом, порядок, в котором вы умножаете матрицы, влияет на результат.
Например, предположите, что вы хотите выполнить операцию, которая масштабирует, переводит, и затем вращает. Принимая R, T и S являются вашими отдельными матрицами преобразования, умножают матрицы можно следующим образом:
C = R*T*S % operations are performed from right to left
S является масштабирующейся матрицей, T является матрицей перевода, R является матрицей вращения, и C является составным объектом этих трех операций. Затем установите свойство Matrix объекта преобразования на C:
hg = hgtransform('Matrix',C);
Следующие наборы операторов не эквивалентны. Первый набор:
hg.Matrix = C; hg.Matrix = eye(4);
результаты в удалении преобразования C. Второй набор:
I = eye(4); C = I*R*T*S; hg.Matrix = C;
применяет преобразование C. Конкатенация единичной матрицы к другим матрицам не имеет никакого эффекта на составную матрицу.
Поскольку операции преобразования заданы в свободных членах (не относительно текущего преобразования), можно отменить серию преобразований путем установки текущего преобразования на единичную матрицу. Например:
hg = hgtransform('Matrix',C); ... hg.Matrix = eye(4);
возвращает объекты, содержавшие объектом преобразования, hg, к их ориентации прежде, чем применить преобразование C.
Для получения дополнительной информации о единичной матрице смотрите, что eye функционирует