Структура опций содержит названные свойства, значения которых передаются bvp4c, и которые влияют на проблемное решение. Используйте эти функции, чтобы создать, изменить, или получить доступ к структуре опций.
Решатель BVP разработан, чтобы обработать системы обыкновенных дифференциальных уравнений
y ′ = f (x, y)
где x является независимой переменной, y является зависимой переменной, и y ′ представляет производную y относительно x dy/dx.
Смотрите Выбирают ODE Solver для получения общей информации об ОДУ.
В краевой задаче решение интереса удовлетворяет определенные граничные условия. Эти условия задают отношение между значениями решения больше чем в одном x. В его базовом синтаксисе bvp4c разработан, чтобы решить двух-точку BVPs, i. e., проблемы, где решение, найденное через определенный интервал [a, b], должно удовлетворить граничные условия
g (y (a), y (b)) = 0
В отличие от задач с начальными значениями, краевая задача не может иметь решения, может иметь конечное число решений или может иметь бесконечно много решений. Как неотъемлемая часть процесса решения BVP, необходимо обеспечить предположение для требуемого решения. Качество этого предположения может быть очень важным для производительности решателя и даже для успешного вычисления.
Могут быть другие трудности при решении BVPs, такие как проблемы, наложенные на бесконечные интервалы или проблемы, которые включают сингулярные коэффициенты. Часто BVPs включают неизвестные параметры p, которые должны быть определены как часть решения проблемы
y ′ = f (x, y, p)
g (y (a), y (b), p) = 0
В этом случае граничные условия должны быть достаточными, чтобы определить значение p.
Функциональный bvp4c решает краевые задачи двух-точки для обыкновенных дифференциальных уравнений (ОДУ). Это интегрирует систему обыкновенных дифференциальных уравнений первого порядка
y ′ = f (x, y)
на интервале [a, b] согласно общим граничным условиям двух-точки
до н.э (y (a), y (b)) = 0
Это может также разместить другие типы проблем BVP, такие как те, которые имеют любое следующее:
Неизвестные параметры
Особенности в решениях
Многоточечные условия
В этом случае количество граничных условий должно быть достаточным, чтобы определить решение и неизвестные параметры.
bvp4c производит решение, которое непрерывно на [a, b] и имеет непрерывную первую производную там. Можно использовать функциональный deval и вывод bvp4c, чтобы оценить решение в отдельных моментах на интервале интегрирования.
bvp4c является кодом конечной разности, который реализует 3-этапную формулу Lobatto IIIa. Это - формула словосочетания, и многочлен словосочетания предоставляет решение C1-continuous, которое является четвертым порядком, точным однородно в интервале интегрирования. Поймайте в сети выбор, и контроль ошибок основаны на невязке непрерывного решения.
Метод словосочетания использует сетку точек, чтобы разделить интервал интегрирования на подынтервалы. Решатель определяет числовое решение путем решения глобальной системы алгебраических уравнений, следующих из граничных условий и условий словосочетания, наложенных на все подынтервалы. Решатель затем оценивает ошибку числового решения на каждом подынтервале. Если решение не удовлетворяет критерии допуска, решатель адаптирует mesh и повторяет процесс. Пользователь должен обеспечить точки начальной mesh, а также начального приближения решения в точках mesh.
Базовый синтаксис решателя BVP
sol = bvp4c(odefun,bcfun,solinit)
Входные параметры
| Указатель на функцию, который оценивает дифференциальные уравнения. Это имеет каноническую форму dydx = odefun(x,y) где | |
| Обработайте к функции, которая оценивает невязку в граничных условиях. Это имеет каноническую форму res = bcfun(ya,yb) где | |
| Структура с полями | |
| Заказанные узлы начальной mesh. Граничные условия наложены в = | |
| Исходное предположение для решения с | |
Структура может иметь любое имя, но поля нужно назвать | ||
Выходным аргументом sol является структура, созданная решателем. В основном случае структура имеет поля x, y, yp и solver.
| Узлы mesh выбраны |
| Приближение к y (x) в точках mesh |
| Приближение к y ′ (x) в точках mesh |
|
|
sol структуры, возвращенный bvp4c, содержит дополнительное поле, если проблема включает неизвестные параметры:
| Значение неизвестных параметров, если есть найденных решателем. |
Функциональный deval использует выходную структуру sol, чтобы оценить числовое решение в любой точке от [a,b].
Для большего количества усовершенствованных приложений можно задать опции решателя путем передачи входного параметра options.
| Структура дополнительных параметров, которые изменяют свойства интегрирования по умолчанию. Это - четвертый входной параметр. sol = bvp4c(odefun,bcfun,solinit,options) Можно создать опции структуры с помощью функционального |
Свойства интегрирования по умолчанию в решателе BVP bvp4c выбраны, чтобы решить типичные проблемы. В некоторых случаях можно улучшить производительность решателя путем переопределения этих значений по умолчанию. Вы делаете это путем предоставления bvp4c структуру options, которая задает одни или несколько значений свойств.
Например, чтобы изменить значение допуска относительной погрешности bvp4c от значения по умолчанию 1e-3 к 1e-4,
Создайте структуру опций с помощью функционального bvpset путем ввода
options = bvpset('RelTol', 1e-4);Передайте структуру options bvp4c можно следующим образом:
sol = bvp4c(odefun,bcfun,solinit,options)
Для полного описания доступных параметров смотрите страницу с описанием для bvpset.
Решение проблемы. Этот пример определяет четвертое собственное значение Уравнения Мэтью. Это иллюстрирует, как записать дифференциальные уравнения второго порядка как систему двух ОДУ первого порядка и как использовать bvp4c, чтобы определить неизвестный параметр λ.
Задача состоит в том, чтобы вычислить четвертое (q = 5) лямбда собственного значения λ уравнения Мэтью
y ′′ + (λ – 2 q, потому что 2x) y = 0
Поскольку неизвестный параметр λ присутствует, это дифференциальное уравнение второго порядка подчиняется трем граничным условиям
y (0) = 1
y ′ (0) = 0
y ′ (π) = 0
Файл, mat4bvp.m, содержит полный код для этого примера. Все функции, требуемые bvp4c, закодированы в этом файле, как вложено или локальных функциях. Чтобы видеть код в редакторе, введите edit mat4bvp в командной строке. Чтобы запустить его, введите mat4bvp в командной строке.
Перепишите проблему как систему первого порядка. Чтобы использовать bvp4c, необходимо переписать уравнения как эквивалентную систему дифференциальных уравнений первого порядка. Используя замену y1 = y и y2 = y ′, дифференциальное уравнение записано как система двух уравнений первого порядка
y1 = y2
y2 = – (λ – 2q, потому что 2x) y1
Обратите внимание на то, что дифференциальные уравнения зависят от неизвестного параметра λ. Граничные условия становятся
y1 (0) – 1 = 0
y2 (0) = 0
y2 (π) = 0
Закодируйте систему ОДУ первого порядка. Если вы представляете уравнение как систему первого порядка, можно закодировать его как функцию, которую может использовать bvp4c. Поскольку существует неизвестный параметр, функция должна иметь форму
dydx = odefun(x,y,parameters)
Следующий код представляет систему в функции, mat4ode. Переменный q совместно используется с внешней функцией:
function dydx = mat4ode(x,y,lambda)
dydx = [ y(2)
-(lambda - 2*q*cos(2*x))*y(1) ];
end % End nested function mat4ode
Закодируйте функцию граничных условий. Необходимо также закодировать граничные условия в функции. Поскольку существует неизвестный параметр, функция должна иметь форму
res = bcfun(ya,yb,parameters)
Код ниже представляет граничные условия в функции, mat4bc.
function res = mat4bc(ya,yb,lambda)
res = [ ya(2)
yb(2)
ya(1)-1 ];
Создайте исходное предположение. Чтобы сформировать структуру предположения solinit с bvpinit, необходимо обеспечить исходные предположения и для решения и для неизвестного параметра.
Функциональный mat4init обеспечивает исходное предположение для решения. mat4init использует y = cos4x, потому что эта функция удовлетворяет граничные условия и имеет правильное качественное поведение (правильное количество изменений знака).
function yinit = mat4init(x)
yinit = [ cos(4*x)
-4*sin(4*x) ];
В вызове bvpinit третий аргумент, lambda, обеспечивает исходное предположение для неизвестного параметра λ.
lambda = 15; solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda);
Этот пример использует символ @, чтобы передать mat4init как указатель на функцию к bvpinit.
Примените решатель BVP. Пример mat4bvp вызывает bvp4c с функциями mat4ode и mat4bc и структура solinit, созданный с bvpinit.
sol = bvp4c(@mat4ode,@mat4bc,solinit);
Просмотрите результаты. Завершите пример путем отображения результатов:
Распечатайте значение неизвестного параметра λ найденный bvp4c.
fprintf('Fourth eigenvalue is approximately %7.3f.\n',...
sol.parameters)Используйте deval, чтобы оценить числовое решение в 100 равномерно распределенных точках в интервале [0, π], и построить график его первого компонента. Этот компонент аппроксимирует y (x).
xint = linspace(0,pi);
Sxint = deval(sol,xint);
plot(xint,Sxint(1,:))
axis([0 pi -1 1.1])
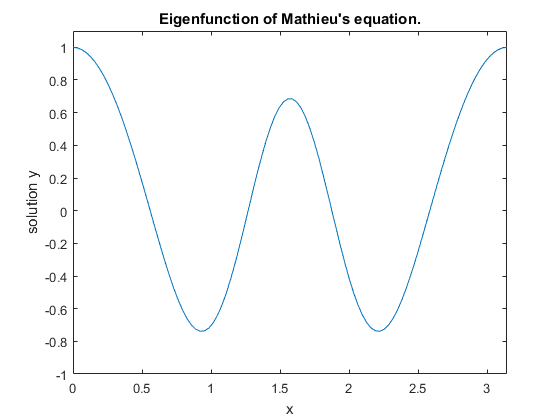
title('Eigenfunction of Mathieu''s equation.')
xlabel('x')
ylabel('solution y')Следующий график показывает собственную функцию, сопоставленную с итоговым собственным значением λ = 17.097.
Нахождение Неизвестных Параметров. Решатель bvp4c может найти неизвестные параметры p для проблем формы
y ′ = f (x, y, p)
до н.э (y (a), y (b), p) = 0
Необходимо предоставить bvp4c исходное предположение для любых неизвестных параметров в векторном solinit.parameters параметры. Когда вы вызовете bvpinit, чтобы создать структуру solinit, задайте исходное предположение как вектор в дополнительном аргументе parameters.
solinit = bvpinit(x,v,parameters)
Аргументы функции bvp4c odefun и bcfun должны каждый иметь третий аргумент.
dydx = odefun(x,y,parameters) res = bcfun(ya,yb,parameters)
При решении дифференциальных уравнений bvp4c настраивает значение неизвестных параметров, чтобы удовлетворить граничные условия. Решатель возвращает окончательные значения этих неизвестных параметров в sol.parameters параметры.
Оценка Решения. Метод коллокации, реализованный в bvp4c, производит решение C1-continuous на целом интервале интегрирования [a, b]. Можно оценить приближенное решение, S (x), в любой точке в [a, b] использование функции помощника deval и структура sol, возвращенный bvp4c.
Sxint = deval(sol,xint)
Функция deval векторизована. Для векторного xint i th столбец Sxint аппроксимирует решение y (xint (i)).
Введение. Чтобы решить краевую задачу, необходимо обеспечить исходное предположение для решения. Качество вашего исходного предположения может быть очень важно для производительности решателя, и для способности решить проблему вообще. Однако придумывание достаточно хорошего предположения может быть самой сложной частью решения краевой задачи. Конечно, необходимо применить знание физического источника проблемы. Часто проблема может быть решена как последовательность относительно более простых проблем, i. e., продолжение.
Этот пример показывает, как использовать продолжение для:
Решите трудный BVP
Проверьте сопоставимое поведение решения
Используя Продолжение, чтобы Решить BVP. Этот пример решает дифференциальное уравнение
εy ′′ + xy ′ = επ2, потому что (πx) – πx грех (πx)
для ε = 10–4, на интервале [–1 1], с граничными условиями y (–1) = –2 и y (1) = 0. Для 0 <ε <1, решение имеет уровень перехода в x = 0. Из-за этого быстрого изменения в решении для маленьких значений ε проблема становится трудной решить численно.
Пример решает проблему как последовательность относительно более простых проблем, i. e., продолжение. Решение одной проблемы используется в качестве исходного предположения для решения следующей проблемы.
Файл, shockbvp.m, содержит полный код для этого примера. Все необходимые функции закодированы как вложенные функции в этом файле. Чтобы видеть код в редакторе, введите edit shockbvp в командной строке. Чтобы запустить его, введите shockbvp в командной строке.
Эта проблема, кажется, в [1] иллюстрирует поддержку выбора mesh хорошо установленного кода BVP COLSYS.
Закодируйте функции граничного условия и ОДУ. Закодируйте дифференциальное уравнение и граничные условия как функции, которые может использовать bvp4c:
Код ниже представляет дифференциальное уравнение и граничные условия в функциях shockODE и shockBC. Обратите внимание на то, что shockODE векторизован, чтобы улучшить производительность решателя. Дополнительный параметр ε представлен e и совместно используется с внешней функцией.
function dydx = shockODE(x,y)
pix = pi*x;
dydx = [ y(2,:)
-x/e.*y(2,:) - pi^2*cos(pix) - pix/e.*sin(pix) ];
end % End nested function shockODE
function res = shockBC(ya,yb)
res = [ ya(1)+2
yb(1) ];
end % End nested function shockBC
Обеспечьте аналитические частные производные. Для этой проблемы решатель извлекает выгоду из использования аналитических частных производных. Код ниже представляет производные в функциях shockJac и shockBCJac.
function jac = shockJac(x,y)
jac = [ 0 1
0 -x/e ];
end % End nested function shockJac
function [dBCdya,dBCdyb] = shockBCJac(ya,yb)
dBCdya = [ 1 0
0 0 ];
dBCdyb = [ 0 0
1 0 ];
end % End nested function shockBCJac
shockJac совместно использует e с внешней функцией.
Скажите bvp4c использовать эти функции, чтобы оценить частные производные путем установки опций FJacobian и BCJacobian. Также установите 'Vectorized' на 'on' указывать, что функция дифференциального уравнения shockODE векторизована.
options = bvpset('FJacobian',@shockJac,...
'BCJacobian',@shockBCJac,...
'Vectorized','on');
Создайте исходное предположение. Необходимо предоставить bvp4c структуру предположения, которая содержит начальную mesh и предположение для значений решения в точках mesh. Постоянное предположение y (x) ≡ 1 и y ′ (x) ≡ 0 и сетка пяти равномерно распределенных точек на [–1 1] достаточно, чтобы решить проблему для ε = 10–2. Используйте bvpinit, чтобы сформировать структуру предположения.
sol = bvpinit([-1 -0.5 0 0.5 1],[1 0]);
Используйте продолжение, чтобы решить проблему. Чтобы получить решение для параметра ε = 10–4, пример использует продолжение путем решения последовательности проблем для ε = 10–2, 10–3, 10–4. Решатель bvp4c не выполняет продолжение автоматически, но пользовательский интерфейс кода, был разработан, чтобы сделать продолжение легким. Код использует вывод sol, который bvp4c производит для одного значения e как предположение в следующей итерации.
e = 0.1;
for i=2:4
e = e/10;
sol = bvp4c(@shockODE,@shockBC,sol,options);
endПросмотрите результаты. Завершите пример путем отображения конечного решения
plot(sol.x,sol.y(1,:))
axis([-1 1 -2.2 2.2])
title(['There is a shock at x = 0 when \epsilon = '...
sprintf('%.e',e) '.'])
xlabel('x')
ylabel('solution y')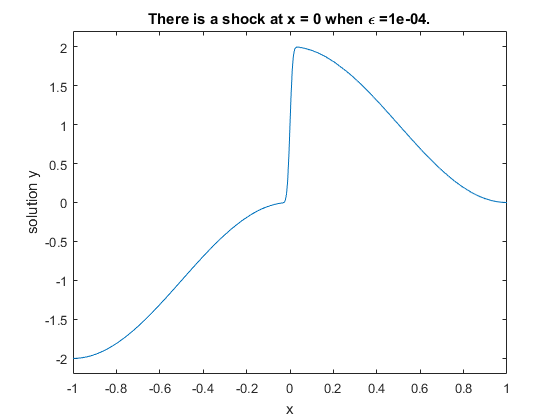
Используя Продолжение, чтобы Проверить Непротиворечивость. Falkner-Skan BVPs является результатом решений для подобия вязкого, несжимаемого, ламинарного течения по плоской пластине. Пример
f ′′′ + и следующие ′′ + β (1 – (f ′) 2) = 0
для β = 0.5 на интервале [0, ∞] с граничными условиями f (0) = 0, f ′ (0) = 0 и f ′ (∞) = 1.
BVP не может быть решен на бесконечном интервале, и это было бы невозможно решить его для даже очень большого конечного интервала. Так, пример пытается решить последовательность проблем, созданных на все больших интервалах, чтобы проверить сопоставимое поведение решения, когда контур приближается к ∞.
Пример налагает бесконечное граничное условие в конечной точке под названием infinity. Пример затем использует продолжение в этой конечной точке, чтобы получить сходимость для все больших значений infinity. Это использует bvpinit, чтобы экстраполировать решение sol для одного значения infinity как исходное предположение для нового значения infinity. График каждого последовательного решения накладывается на те из предыдущих решений, таким образом, они могут легко быть сравнены для непротиворечивости.
Файл, fsbvp.m, содержит полный код для этого примера. Все необходимые функции закодированы как вложенные функции в этом файле. Чтобы видеть код в редакторе, введите edit fsbvp в командной строке. Чтобы запустить его, введите fsbvp в командной строке.
Закодируйте функции граничного условия и ОДУ. Закодируйте дифференциальное уравнение и граничные условия как функции, которые может использовать bvp4c. Проблемный параметр beta совместно используется с внешней функцией.
function dfdeta = fsode(eta,f)
dfdeta = [ f(2)
f(3)
-f(1)*f(3) - beta*(1 - f(2)^2) ];
end % End nested function fsode
function res = fsbc(f0,finf)
res = [f0(1)
f0(2)
finf(2) - 1];
end % End nested function fsbc
Создайте исходное предположение. Необходимо предоставить bvp4c структуру предположения, которая содержит начальную mesh и предположение для значений решения в точках mesh. Грубая сетка пяти точек и постоянного предположения, которое удовлетворяет граничные условия, достаточно хороша, чтобы получить сходимость когда infinity = 3.
infinity = 3; maxinfinity = 6; solinit = bvpinit(linspace(0,infinity,5),[0 0 1]);
Решите на начальном интервале. Пример получает решение для infinity = 3. Это затем распечатывает вычисленное значение f ′′ (0) для сравнения со значением, о котором сообщает Чебечи и Келлер [2]:
sol = bvp4c(@fsode,@fsbc,solinit);
eta = sol.x;
f = sol.y;
fprintf('\n');
fprintf('Cebeci & Keller report that f''''(0) = 0.92768.\n')
fprintf('Value computed using infinity = %g is %7.5f.\n', ...
infinity,f(3,1))
Печать в качестве примера
Cebeci & Keller report that f''(0) = 0.92768. Value computed using infinity = 3 is 0.92915.
Setup фигура и график начальное решение.
figure
plot(eta,f(2,:),eta(end),f(2,end),'o');
axis([0 maxinfinity 0 1.4]);
title('Falkner-Skan equation, positive wall shear, \beta = 0.5.')
xlabel('\eta')
ylabel('df/d\eta')
hold on
drawnow
shg
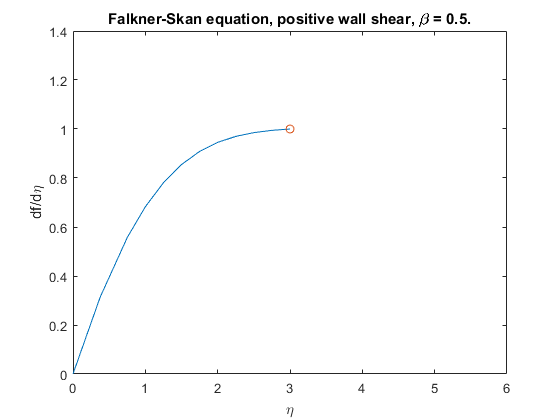
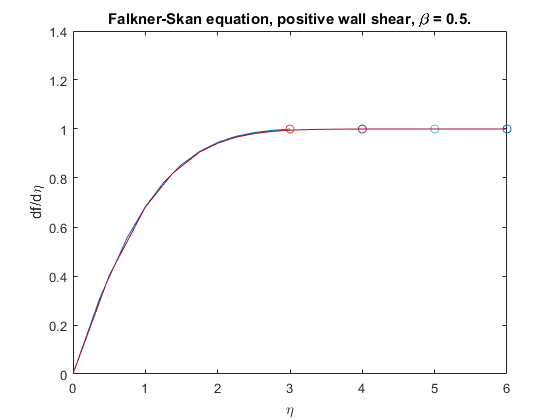
Используйте продолжение, чтобы решить проблему и построить график последующих решений. Пример затем решает проблему для infinity = 4, 5, 6. Это использует bvpinit, чтобы экстраполировать решение sol для одного значения infinity как исходное предположение для следующего значения infinity. Для каждой итерации пример распечатывает вычисленное значение f ′′ (0) и накладывает график решения в существующей фигуре.
for Bnew = infinity+1:maxinfinity
solinit = bvpinit(sol,[0 Bnew]); % Extend solution to Bnew.
sol = bvp4c(@fsode,@fsbc,solinit);
eta = sol.x;
f = sol.y;
fprintf('Value computed using infinity = %g is %7.5f.\n', ...
Bnew,f(3,1))
plot(eta,f(2,:),eta(end),f(2,end),'o');
drawnow
end
hold off
Печать в качестве примера
Value computed using infinity = 4 is 0.92774. Value computed using infinity = 5 is 0.92770. Value computed using infinity = 6 is 0.92770.
Обратите внимание на то, что значения приближаются 0.92768, как сообщил Чебечи и Келлер. Наложенные графики подтверждают непротиворечивость поведения решения.
Введение. Функция bvp4c решает класс сингулярного BVPs формы
| (1) |
Это может также разместить неизвестные параметры для проблем формы
Сингулярные проблемы должны быть созданы через определенный интервал [0, b] с b> 0. Используйте bvpset, чтобы передать постоянную матрицу S bvp4c как значение свойства интегрирования 'SingularTerm'. Граничные условия в x = 0 должны быть сопоставимы с необходимым условием для сглаженного решения, Sy (0) = 0. Исходное предположение должно также удовлетворить это необходимое условие.
Когда вы решаете сингулярное использование BVP
sol = bvp4c(@odefun,@bcfun,solinit,options)
bvp4c требует, чтобы ваш функциональный odefun(x,y) возвратил только значение f (x, y) термин в Уравнении 5-2.
Уравнение Эмдена. Уравнение Эмдена возникает в моделировании сферического тела газа. УЧП модели уменьшается симметрией до ОДУ
через определенный интервал [0,1]. Коэффициент 2/x сингулярен в x = 0, но симметрия подразумевает граничное условие y ′ (0) = 0. С этим граничным условием, термином
четко определено, когда x приближается 0. Для граничного условия , этот BVP имеет аналитическое решение
Файл, emdenbvp.m, содержит полный код для этого примера. Это содержит все необходимые функции, закодированные как локальные функции. Чтобы видеть код в редакторе, введите edit emdenbvp в командной строке. Чтобы запустить его, введите emdenbvp в командной строке.
Перепишите проблему как систему первого порядка и идентифицируйте сингулярный термин. Используя замену y1 = y и y2 = y ′, запишите дифференциальное уравнение как систему двух уравнений первого порядка
Граничные условия становятся
Запись системы ОДУ в векторной матричной форме
условия Уравнения 5-2 идентифицированы как
и
Закодируйте функции граничного условия и ОДУ. Закодируйте дифференциальное уравнение и граничные условия как функции, которые может использовать bvp4c.
function dydx = emdenode(x,y)
dydx = [ y(2)
-y(1)^5 ];
function res = emdenbc(ya,yb)
res = [ ya(2)
yb(1) - sqrt(3)/2 ];
Свойства интегрирования Setup. Используйте матрицу в качестве значения свойства интегрирования 'SingularTerm'.
S = [0,0;0,-2];
options = bvpset('SingularTerm',S);
Создайте исходное предположение. Этот пример запускается с сетки пяти точек и постоянного предположения для решения.
Используйте bvpinit, чтобы сформировать структуру предположения
guess = [sqrt(3)/2;0]; solinit = bvpinit(linspace(0,1,5),guess);
Решите проблему. Используйте стандартный синтаксис bvp4c, чтобы решить проблему.
sol = bvp4c(@emdenode,@emdenbc,solinit,options);
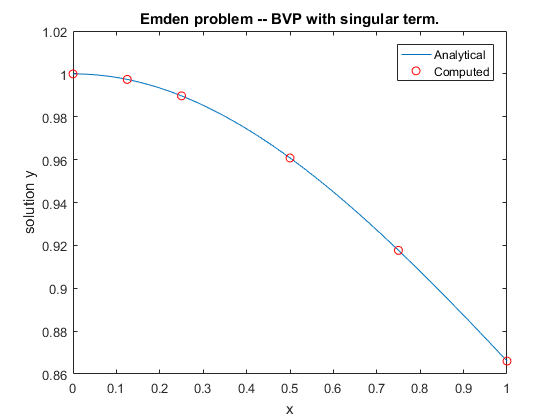
Просмотрите результаты. Эта проблема имеет аналитическое решение
Пример оценивает аналитическое решение в 100 равномерно распределенных точках и строит график его наряду с числовым решением, вычисленным с помощью bvp4c.
x = linspace(0,1);
truy = 1 ./ sqrt(1 + (x.^2)/3);
plot(x,truy,sol.x,sol.y(1,:),'ro');
title('Emden problem -- BVP with singular term.')
legend('Analytical','Computed');
xlabel('x');
ylabel('solution y');
В многоточечных краевых задачах решение интереса удовлетворяет условия в точках в интервале интегрирования. Функция bvp4c полезна в решении таких проблем.
Следующий пример показывает, как многоточечная возможность в bvp4c может повысить эффективность, когда вы решаете несглаженную проблему. Следующие уравнения решены на 0 ≤ x ≤ λ для постоянных параметров n, κ, λ> 1, и η = λ2 / (n × κ2). Они подчиняются граничным условиям v(0) = 0 и C (λ) = 1:
v' = (C - 1)/n
C' = (v * C - min(x,1))/
Термин min(x,1) не сглажен в xc = 1, и это может влиять на эффективность решателя. Путем представления интерфейсной точки в xc = 1 сглаженные решения могут быть получены на [0,1] и [1, λ]. Чтобы получить непрерывное решение на целом интервале [0, λ], пример налагает соответствие с условиями в интерфейсе.
Файл, threebvp.m, содержит полный код для этого примера, и это решает проблему для λ = 2, n = 0.05 и нескольких значений κ. Все необходимые функции закодированы как вложенные функции в threebvp.m m. Чтобы видеть код в редакторе, введите edit threebvp в командной строке. Чтобы запустить его, введите threebvp в командной строке.
Пример берет вас через следующие шаги:
Определите интерфейсы и разделите интервал интегрирования в области. Представление интерфейсной точки в xc = 1 делит проблему на две области, в которых решения остаются сглаженными. Дифференциальные уравнения для этих двух областей
Область 1: 0 ≤ x ≤ 1
v' = (C - 1)/n
C' = (v * C - x)/
Область 2: 1 ≤ x ≤ λ
v' = (C - 1)/n
C' = (v * C - 1)/
Обратите внимание на то, что интерфейс xc = 1 включен в обе области. В xc = 1 bvp4c производит левое и правое решение. Эти решения обозначены как v(1-), C(1-) и v(1+), C(1+) соответственно.
Определите граничные условия. Решение двух дифференциальных уравнений первого порядка в двух областях требует наложения четырех граничных условий. Два из этих условий прибывают из исходной формулировки; другие осуществляют непрерывность решения через интерфейс xc = 1:
v(0) = 0
C() - 1 = 0
v(1-) - v(1+) = 0
C(1-) - C(1+) = 0
Здесь, v(1-), C(1-) и v(1+), C(1+) обозначают левое и правое решение в интерфейсе.
Закодируйте производную функцию. В производной функции y(1) соответствует v(x), и y(2) соответствует C(x). Дополнительный region входного параметра идентифицирует область, в которой оценена производная. bvp4c перечисляет области слева направо, начиная с 1. Обратите внимание на то, что проблемные параметры n и η совместно используются с внешней функцией:
function dydx = f(x,y,region)
dydx = zeros(2,1);
dydx(1) = (y(2) - 1)/n;
% The definition of C'(x) depends on the region.
switch region
case 1 % x in [0 1]
dydx(2) = (y(1)*y(2) - x)/;
case 2 % x in [1 ]
dydx(2) = (y(1)*y(2) - 1)/;
end
end % End nested function f
Закодируйте функцию граничных условий. Для многоточечного BVPs аргументы функции граничных условий, YL и YR, становятся матрицами. В частности, k th столбец YL(:,k) представляет решение на левом контуре k th область. Точно так же YR(:,k) представляет решение на правильном контуре k th область.
В примере, y (0) аппроксимирован YL(:,1), в то время как y (λ) аппроксимирован YR(:,end) конец. Непрерывность решения во внутреннем интерфейсе требует того YR(:,1) = YL(:,2). Вложенная функция bc вычисляет невязку в граничных условиях:
function res = bc(YL,YR)
res = [YL(1,1) % v(0) = 0
YR(1,1) - YL(1,2) % Continuity of v(x) at x=1
YR(2,1) - YL(2,2) % Continuity of C(x) at x=1
YR(2,end) - 1]; % C() = 1
end % End nested function bc
Создайте исходное предположение. Для многоточечного BVPs, при создании исходного предположения с помощью bvpinit, двойных записей использования в xinit для интерфейсной точки xc. Этот пример использует постоянное предположение yinit = [1;1]:
xc = 1; xinit = [0, 0.25, 0.5, 0.75, xc, xc, 1.25, 1.5, 1.75, 2]; solinit = bvpinit(xinit,yinit)
Для многоточечного BVPs можно использовать различные предположения в различных областях. Чтобы сделать это, вы задаете исходное предположение для y как функция с помощью следующего синтаксиса:
solinit = bvpinit(xinit,@yinitfcn)
Функция исходного предположения должна иметь следующую общую форму:
function y = yinitfcn(x,region)
switch region
case 1 % x in [0, 1]
y = [1;1]; % initial guess for y(x)
case 2 % x in [1, ]
y = [1;1]; % initial guess for y(x),
end
Примените решатель. Функция bvp4c использует тот же синтаксис для многоточечного BVPs, как это делает для двух-точки BVPs:
sol = bvp4c(@f,@bc,solinit);
Точки mesh, возвращенные в sol.x, адаптируются к поведению решения, но mesh все еще включает двойной ввод для интерфейсной точки xc = 1. Соответствующие столбцы sol.y представляют левое и правое решение в xc.
Просмотрите результаты. Используя deval, решение может быть оценено в любой точке в интервале интегрирования.
Обратите внимание на то, что, с левыми и правыми значениями, вычисленными в интерфейсе, решение исключительно не задано в xc = 1. При оценке решения точно в интерфейсе, deval выдает предупреждение и возвращает среднее число левых и правых значений решения. Вызовите deval в xc-eps(xc) и xc+eps(xc), чтобы получить предельные значения в xc.
Пример строит график решения, аппроксимированного в точках mesh, выбранных решателем:
plot(sol.x,sol.y(1,:),sol.x,sol.y(2,:),'--')
legend('v(x)','C(x)')
title(['A three-point BVP solved with BVP4C'])
xlabel(['\lambda = 2, \kappa = 5.'])
ylabel('v and C')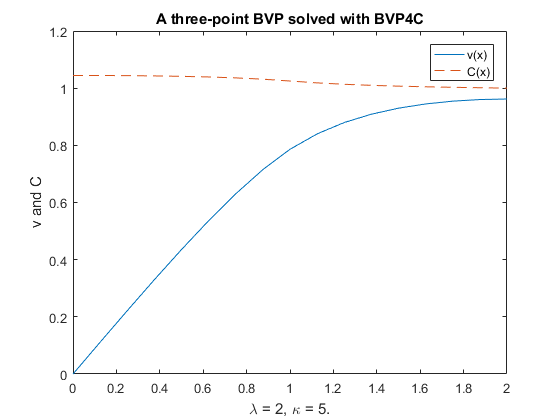
Следующие дополнительные примеры доступны. Ввод
edit examplename
просмотреть код и
examplename
запускать пример.
Имя в качестве примера | Описание |
|---|---|
| Уравнение Эмдена, сингулярный BVP |
| Falkner-Skan BVP на бесконечном интервале |
| Четвертая собственная функция уравнения Мэтью |
| Решение с уровнем шока рядом x = 0 |
| BVP точно с двумя решениями |
| Краевая задача с тремя точками |
Для дополнительных примеров см. Пример при Решении BVPs с BVP4C.
[1] Ascher, U., R. Mattheij и Р. Рассел, “Числовое Решение Краевых задач для Обыкновенных дифференциальных уравнений”, SIAM, Филадельфия, PA, 1995, p. 372.
[2] Cebeci, T. и Х. B. Келлер, "Стреляя и Параллельные Методы Стрельбы для Решения Уравнения пограничного слоя Falkner-Skan", J. Аккомпанируйте Физике, Изданию 7, 1971, стр 289-300.