Триангуляции Делоне широко используются в научных вычислениях во многих разнообразных приложениях. В то время как существуют многочисленные алгоритмы для вычислительных триангуляций, это - благоприятные геометрические свойства Триангуляции Делоне, которые делают его настолько полезным.
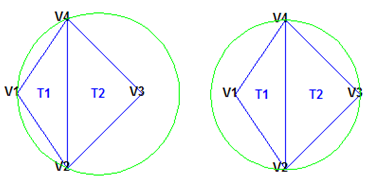
Основное свойство является критерием Delaunay. В случае 2D триангуляций это часто называется пустым критерием описанного круга. Для набора точек в 2D Триангуляция Делоне этих точек гарантирует, что описанный круг, сопоставленный с каждым треугольником, не содержит никакую другую точку в своей внутренней части. Это свойство важно. На иллюстрации ниже, описанный круг, сопоставленный с T1, пуст. Это не содержит точку в своей внутренней части. Описанный круг, сопоставленный с T2, пуст. Это не содержит точку в своей внутренней части. Этой триангуляцией является Триангуляция Делоне.
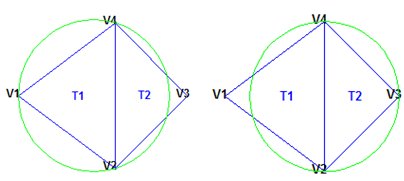
Треугольники ниже отличаются. Описанный круг, сопоставленный с T1, не пуст. Это содержит V3 в своей внутренней части. Описанный круг, сопоставленный с T2, не пуст. Это содержит V1 в своей внутренней части. Этой триангуляцией не является Триангуляция Делоне.
Треугольники Delaunay, как говорят, “хорошо формируются”, потому что в выполнении пустого свойства описанного круга, треугольники с большими внутренними углами выбраны по единицам с маленькими внутренними углами. Треугольники в нетриангуляции Делоне имеют резкие углы в вершинах V2 и V4. Если бы край, {V2, V4} был заменен краем, соединяющим V1 и V3, минимальный угол, был бы максимизирован, и триангуляция станет Триангуляцией Делоне. Кроме того, Триангуляция Делоне соединяет точки способом ближайшего соседа. Эти две характеристики, хорошо сложенные треугольники и отношение ближайшего соседа, имеют важные последствия на практике и мотивируют использование Триангуляций Делоне в интерполяции данных, имеющий разброс.
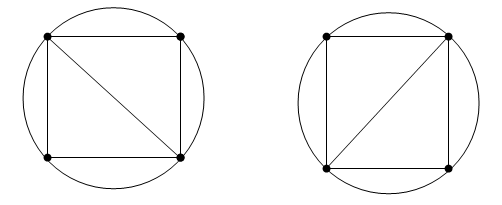
В то время как свойство Delaunay четко определено, топология триангуляции не уникальна в присутствии вырожденных наборов точки. В двух измерениях степени вырождения возникают, когда четыре или больше уникальных точки лежат на том же круге. Вершины квадрата, например, имеют групповую Триангуляцию Делоне.
Свойства Триангуляций Делоне расширяют к более высоким размерностям. Триангуляция 3-D набора точек состоит из tetrahedra. Следующая иллюстрация показывает простую 3-D Триангуляцию Делоне, составленную из двух tetrahedra. Описанная сфера одного четырехгранника, как показывают, подсвечивает пустой критерий описанной сферы.
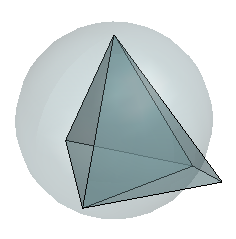
3-D Триангуляция Делоне производит tetrahedra, которые удовлетворяют пустой критерий описанной сферы.
MATLAB® обеспечивает два способа создать Триангуляции Делоне:
Функции delaunay и delaunayn
Класс delaunayTriangulation
Функция delaunay поддерживает создание 2D и 3-D Триангуляций Делоне. Поддержки функции delaunayn, создающие Триангуляции Делоне в 4-D и выше.
Создание Триангуляций Делоне в размерностях выше, чем 6-D обычно не практично для умеренного к большим наборам точки из-за экспоненциального роста в необходимой памяти.
Поддержки класса delaunayTriangulation, создающие Триангуляции Делоне в 2D и 3-D. Это предоставляет много методов, которые полезны для разработки основанных на триангуляции алгоритмов. Эти методы класса похожи на функции, но они ограничиваются, чтобы работать с триангуляциями, созданными с помощью delaunayTriangulation. Класс delaunayTriangulation также поддерживает создание связанных построений, таких как выпуклая оболочка и Диаграмма Вороного. Это также поддерживает создание ограниченных Триангуляций Делоне.
Таким образом:
Функция delaunay полезна, когда вы только требуете основных данных триангуляции и этого, данные достаточно завершены для вашего приложения.
Класс delaunayTriangulation предлагает больше функциональности для разработки основанных на триангуляции приложений. Полезно, когда вы требуете триангуляции, и вы хотите выполнить любую из этих операций:
Ищите триангуляцию треугольники или tetrahedra включение точки запроса.
Используйте триангуляцию, чтобы выполнить поиск точки ближайшего соседа.
Запросите топологическую смежность триангуляции или геометрические свойства.
Измените триангуляцию, чтобы вставить или удалить точки.
Ограничьте края в триангуляции — это называется ограниченной Триангуляцией Делоне.
Триангулируйте полигон и опционально удалите треугольники, которые являются за пределами области.
Используйте Триангуляцию Делоне, чтобы вычислить выпуклую оболочку или Диаграмму Вороного.
delaunay и функции delaunayn берут набор точек и производят триангуляцию в матричном формате. Обратитесь к Матричному Формату Триангуляции для получения дополнительной информации об этой структуре данных. В 2D функция delaunay часто используется, чтобы произвести триангуляцию, которая может использоваться, чтобы построить график поверхности, заданной с точки зрения набора точек данных, имеющий разброс. В этом приложении важно отметить, что этот подход может только использоваться, если поверхность однозначна. Например, это не могло использоваться, чтобы построить график сферической поверхности, потому что существует два значения z, соответствующие синглу (x, y) координата. Простой пример демонстрирует, как функция delaunay может использоваться, чтобы построить график поверхности, представляющей набор выборочных данных.
Этот пример показывает, как использовать функцию delaunay, чтобы создать 2D Триангуляцию Делоне из набора данных подводной горы. Подводная гора является подводной горой. Набор данных состоит из набора долготы (x) и широта (y) местоположения и соответствующие повышения подводной горы (z), измеренный в тех координатах.
Загрузите набор данных подводной горы и просмотрите (x, y) данные как график рассеивания.
load seamount plot(x,y,'.','markersize',12) xlabel('Longitude'), ylabel('Latitude') grid on

Создайте Триангуляцию Делоне из этого набора точки и используйте triplot, чтобы построить график триангуляции в существующей фигуре.
tri = delaunay(x,y); hold on, triplot(tri,x,y), hold off

Добавьте данные глубины (z) с подводной горы, чтобы снять вершины и создать поверхность. Создайте новую фигуру и используйте trimesh, чтобы построить график поверхности в каркасном режиме.
figure hidden on trimesh(tri,x,y,z) xlabel('Longitude'),ylabel('Latitude'),zlabel('Depth in Feet');

Если вы хотите построить график поверхности в теневом режиме, используйте trisurf вместо trimesh.
3-D Триангуляция Делоне также может быть создана с помощью функции delaunay. Эта триангуляция состоит из tetrahedra.
Этот пример показывает, как создать 3-D Триангуляцию Делоне случайного набора данных. Триангуляция построена график с помощью tetramesh, и опция FaceAlpha добавляет прозрачность к графику.
X = gallery('uniformdata',[30 3],0); tet = delaunay(X); faceColor = [0.6875 0.8750 0.8984]; tetramesh(tet,X,'FaceColor', faceColor,'FaceAlpha',0.3);

MATLAB обеспечивает функцию delaunayn, чтобы поддержать создание Триангуляций Делоне в размерности 4-D и выше. Две дополнительных функции tsearchn и dsearchn также обеспечиваются, чтобы поддержать пространственный поиск триангуляций N-D. Смотрите Пространственный Поиск для получения дополнительной информации об основанном на триангуляции поиске.
Класс delaunayTriangulation обеспечивает другой способ создать Триангуляции Делоне в MATLAB. В то время как delaunay и delaunayTriangulation используют тот же базовый алгоритм и производят ту же триангуляцию, delaunayTriangulation предоставляет дополнительные методы, которые полезны для разработки находящихся в Delaunay алгоритмов. Эти методы похожи на функции, которые группированы вместе с данными триангуляции в контейнер, названный классом. Держание вместе всего в классе обеспечивает более организованную настройку, которая улучшает простоту использования. Это также улучшает производительность основанных на триангуляции поисковых запросов, таких как местоположение точки и ближайшего соседа. delaunayTriangulation поддерживает инкрементное редактирование Триангуляции Делоне. Также можно наложить граничные ограничения в 2D.
Представления триангуляции представляют класс triangulation, который поддерживает топологические и геометрические запросы для 2D и 3-D триангуляций. delaunayTriangulation является специальным видом triangulation. Это означает, что можно выполнить любой запрос triangulation на delaunayTriangulation в дополнение к Delaunay-специфичным запросам. В более формальных терминах языка MATLAB delaunayTriangulation является подклассом triangulation.
Этот пример показывает, как создать, запросить, и отредактировать Триангуляцию Делоне от данных seamount с помощью delaunayTriangulation. Набор данных подводной горы содержит (x, y) местоположения и соответствующие повышения (z), которые задают поверхность подводной горы.
Загрузите и триангулируйте (x, y) данные.
load seamount
DT = delaunayTriangulation(x,y)DT =
delaunayTriangulation with properties:
Points: [294x2 double]
ConnectivityList: [566x3 double]
Constraints: []
Свойство Constraints пусто, потому что нет никаких наложенных граничных ограничений. Свойство Points представляет координаты вершин, и свойство ConnectivityList представляет треугольники. Вместе, эти два свойства задают матричные данные для триангуляции.
Класс delaunayTriangulation является оберткой вокруг матричных данных, и он предлагает набор дополнительных методов. Вы получаете доступ к свойствам в delaunayTriangulation таким же образом, вы получаете доступ к полям struct.
Доступ к данным вершины.
DT.Points;
Доступ к данным возможности соединения.
DT.ConnectivityList;
Доступ к первому треугольнику в свойстве ConnectivityList.
DT.ConnectivityList(1,:)
ans = 1×3
205 230 262
delaunayTriangulation обеспечивает простой способ индексировать в матрицу свойства ConnectivityList.
Доступ к первому треугольнику.
DT(1,:)
ans = 1×3
205 230 262
Исследуйте первую вершину первого треугольника.
DT(1,1)
ans = 205
Исследуйте все треугольники в триангуляции.
DT(:,:);
Индексируя в delaunayTriangulation вывод, DT, работает как индексация в массив триангуляции вывод от delaunay. Различием между этими двумя являются дополнительные методы, что можно обратиться к DT (например, nearestNeighbor и pointLocation).
Используйте triplot, чтобы построить график delaunayTriangulation. Функция triplot не является методом delaunayTriangulation, но она принимает и может построить график delaunayTriangulation.
triplot(DT); axis equal xlabel('Longitude'), ylabel('Latitude') grid on

Также вы могли использовать triplot(DT(:,:), DT.Points(:,1), DT.Points(:,2));, чтобы получить тот же график.
Используйте метод delaunayTriangulation, convexHull, чтобы вычислить выпуклую оболочку и добавить его к графику. Поскольку у вас уже есть Триангуляция Делоне, этот метод позволяет вам выводить выпуклую оболочку более эффективно, чем полное вычисление с помощью convhull.
hold on k = convexHull(DT); xHull = DT.Points(k,1); yHull = DT.Points(k,2); plot(xHull,yHull,'r','LineWidth',2); hold off

Можно инкрементно отредактировать delaunayTriangulation, чтобы добавить или удалить точки. Если необходимо добавить точки к существующей триангуляции, то инкрементное сложение быстрее, чем полная перетриангуляция увеличенного набора точки. Инкрементное удаление точек более эффективно, когда число точек, которое будет удалено, является маленьким относительно существующего числа точек.
Отредактируйте триангуляцию, чтобы удалить точки на выпуклой оболочке от предыдущего вычисления.
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on % The convex hull topology duplicates the start and end vertex. % Remove the duplicate entry. k(end) = []; % Now remove the points on the convex hull. DT.Points(k,:) = []
DT =
delaunayTriangulation with properties:
Points: [274x2 double]
ConnectivityList: [528x3 double]
Constraints: []
% Plot the new triangulation. hold on triplot(DT); hold off

Существует одна вершина, которая является только в контуре выпуклой оболочки, которая не была демонтирована. То, что это является внутренним к оболочке, может быть замечено использующее инструмент Zoom-In в фигуре. Вы могли построить график меток вершины, чтобы определить индекс этой вершины и удалить его из триангуляции. Также можно использовать метод nearestNeighbor, чтобы идентифицировать индекс с большей готовностью.
Точка близко к местоположению (211.6,-48.15). Используйте nearestNeighbor метод, чтобы найти самую близкую вершину.
vertexId = nearestNeighbor(DT, 211.6, -48.15)
vertexId = 50
Теперь удалите ту вершину из триангуляции.
DT.Points(vertexId,:) = []
DT =
delaunayTriangulation with properties:
Points: [273x2 double]
ConnectivityList: [525x3 double]
Constraints: []
Постройте график новой триангуляции.
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on hold on triplot(DT); hold off

Добавьте точки к существующей триангуляции. Добавьте 4 точки, чтобы сформировать прямоугольник вокруг триангуляции.
Padditional = [210.9 -48.5; 211.6 -48.5; ...
211.6 -47.9; 210.9 -47.9];
DT.Points(end+(1:4),:) = PadditionalDT =
delaunayTriangulation with properties:
Points: [277x2 double]
ConnectivityList: [548x3 double]
Constraints: []
Закройте все существующие фигуры.
close allПостройте график новой триангуляции.
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on hold on triplot(DT); hold off

Можно отредактировать точки в триангуляции, чтобы переместить их в новое местоположение. Отредактируйте первый из дополнительного набора точки (вершина ID 274).
DT.Points(274,:) = [211 -48.4];
Закройте все существующие фигуры.
close allПостройте график новой триангуляции
figure plot(xHull,yHull,'r','LineWidth',2); axis equal xlabel('Longitude'),ylabel('Latitude') grid on hold on triplot(DT); hold off

Используйте метод класса triangulation, vertexAttachments, чтобы найти присоединенные треугольники. Поскольку количество треугольников, присоединенных к вершине, является переменным, метод возвращает присоединенные треугольные идентификаторы в массиве ячеек. Вам нужны фигурные скобки, чтобы извлечь содержимое.
attTris = vertexAttachments(DT,274); hold on triplot(DT(attTris{:},:),DT.Points(:,1),DT.Points(:,2),'g') hold off

delaunayTriangulation также может использоваться, чтобы триангулировать точки на 3-D пробеле. Получившаяся триангуляция состоит из tetrahedra.
Этот пример показывает, как использовать delaunayTriangulation, чтобы создать и построить график триангуляции 3-D точек.
P = gallery('uniformdata',30,3,0);
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [30x3 double]
ConnectivityList: [117x4 double]
Constraints: []
faceColor = [0.6875 0.8750 0.8984]; tetramesh(DT,'FaceColor', faceColor,'FaceAlpha',0.3);

Функция tetramesh строит график и внутренних и внешних поверхностей триангуляции. Для больших 3-D триангуляций, строя график внутренних поверхностей может быть ненужное использование ресурсов. График граничной силы быть более соответствующим. Можно использовать метод freeBoundary, чтобы получить граничную триангуляцию в матричном формате. Затем передайте результат trimesh или trisurf.
Класс delaunayTriangulation позволяет вам ограничивать края в 2D триангуляции. Это означает, что можно выбрать пару точек в триангуляции и ограничить край соединять те точки. Можно изобразить это как “принуждение” края между одной или несколькими парами точек. Следующий пример показывает, как граничные ограничения могут влиять на триангуляцию.
Триангуляцией ниже является Триангуляция Делоне, потому что она уважает пустой критерий описанного круга.

Триангулируйте набор точек с граничным ограничением, заданным между вершиной V1 и V3.
Задайте набор точки.
P = [2 4; 6 1; 9 4; 6 7];
Задайте ограничение, C, между V1 и V3.
C = [1 3]; DT = delaunayTriangulation(P,C);
Постройте график триангуляции и добавьте аннотации.
triplot(DT) % Label the vertices. hold on numvx = size(P,1); vxlabels = arrayfun(@(n) {sprintf('V%d', n)}, (1:numvx)'); Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, 'FontWeight', ... 'bold', 'HorizontalAlignment','center', 'BackgroundColor', ... 'none'); hold off % Use the incenters to find the positions for placing triangle labels on the plot. hold on IC = incenter(DT); numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off % Plot the circumcircle associated with the triangle, T1. hold on [CC,r] = circumcenter(DT); theta = 0:pi/50:2*pi; xunit = r(1)*cos(theta) + CC(1,1); yunit = r(1)*sin(theta) + CC(1,2); plot(xunit,yunit,'g'); axis equal hold off

Ограничение между вершинами (V1, V3) соблюдалось, однако, критерий Delaunay делался недействительным. Это также делает недействительным отношение ближайшего соседа, которое свойственно от Триангуляции Делоне. Это означает, что метод поиска nearestNeighbor, обеспеченный delaunayTriangulation, не может быть поддержан, если триангуляция имеет ограничения.
В типовых приложениях триангуляция может состоять из многих точек, и относительно небольшое количество краев в триангуляции может быть ограничено. Такая триангуляция, как говорят, локально non-Delaunay, потому что много треугольников в триангуляции могут уважать критерий Delaunay, но локально могут быть некоторые треугольники, которые не делают. Во многих приложениях локальная релаксация пустого свойства описанного круга не является беспокойством.
Ограниченные триангуляции обычно используются, чтобы триангулировать невыпуклый полигон. Ограничения дают нам соответствие между краями полигона и краями триангуляции. Это отношение позволяет вам извлечь триангуляцию, которая представляет область. Следующий пример показывает, как использовать ограниченный delaunayTriangulation, чтобы триангулировать невыпуклый полигон.
Задайте и постройте график полигона.
figure() axis([-1 17 -1 6]); axis equal P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; patch(P(:,1),P(:,2),'-r','LineWidth',2,'FaceColor',... 'none','EdgeColor','r'); % Label the points. hold on numvx = size(P,1); vxlabels = arrayfun(@(n) {sprintf('P%d', n)}, (1:numvx)'); Hpl = text(P(:,1)+0.2, P(:,2)+0.2, vxlabels, 'FontWeight', ... 'bold', 'HorizontalAlignment','center', 'BackgroundColor', ... 'none'); hold off

Создайте и постройте график триангуляции вместе с контуром полигона.
figure() subplot(2,1,1); axis([-1 17 -1 6]); axis equal P = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5]; DT = delaunayTriangulation(P); triplot(DT) hold on; patch(P(:,1),P(:,2),'-r','LineWidth',2,'FaceColor',... 'none','EdgeColor','r'); hold off % Plot the standalone triangulation in a subplot. subplot(2,1,2); axis([-1 17 -1 6]); axis equal triplot(DT)

Эта триангуляция не может использоваться, чтобы представлять область полигона, потому что некоторые треугольники сокращали через контур. Необходимо наложить ограничение на края, которые сокращаются краями триангуляции. Поскольку все края нужно уважать, необходимо ограничить все края. Шаги ниже показа, как ограничить все края.
Введите ограниченное граничное определение. Наблюдайте от аннотируемой фигуры, где вам нужны ограничения (между (V1, V2), (V2, V3), и так далее).
C = [1 2; 2 3; 3 4; 4 5; 5 6; 6 7; 7 8; 8 1];
В целом, если у вас есть точки N в последовательности, которые задают многоугольный контур, ограничения могут быть выражены как C = [(1:(N-1))' (2:N)'; N 1];.
Задайте ограничения, когда вы создадите delaunayTriangulation.
DT = delaunayTriangulation(P,C);
Также можно наложить ограничения на существующую триангуляцию путем установки свойства Constraints: DT.Constraints = C;.
Постройте график триангуляции и полигона.
figure('Color','white') subplot(2,1,1); axis([-1 17 -1 6]); axis equal triplot(DT) hold on; patch(P(:,1),P(:,2),'-r','LineWidth',2, ... 'FaceColor','none','EdgeColor','r'); hold off % Plot the standalone triangulation in a subplot. subplot(2,1,2); axis([-1 17 -1 6]); axis equal triplot(DT)

График показывает, что края триангуляции уважают контур полигона. Однако триангуляция заполняет вогнутости. То, что необходимо, является триангуляцией, которая представляет многоугольную область. Можно извлечь треугольники в полигоне с помощью метода delaunayTriangulation, isInterior. Этот метод возвращает логический массив, true которого и значения false, которые указывают, являются ли треугольники в ограниченной геометрической области. Анализ основан на теореме Кривой Жорданы, и контуры заданы граничными ограничениями. ith треугольник в триангуляции считается в области, если ith логический флаг верен, в противном случае это снаружи.
Теперь используйте метод isInterior, чтобы вычислить и построить график набора доменных треугольников.
% Plot the constrained edges in red. figure('Color','white') subplot(2,1,1); plot(P(C'),P(C'+size(P,1)),'-r','LineWidth', 2); axis([-1 17 -1 6]); % Compute the in/out status. IO = isInterior(DT); subplot(2,1,2); hold on; axis([-1 17 -1 6]); % Use triplot to plot the triangles that are inside. % Uses logical indexing and dt(i,j) shorthand % format to access the triangulation. triplot(DT(IO, :),DT.Points(:,1), DT.Points(:,2),'LineWidth', 2) hold off;

Алгоритмы Delaunay в MATLAB создают триангуляцию из уникального набора точек. Если точки, переданные функции триангуляции или классу, не уникальны, дублирующиеся местоположения обнаруживаются, и дублирующаяся точка проигнорирована. Это производит триангуляцию, которая не ссылается на некоторые точки в исходном входном параметре, а именно, дублирующиеся точки. Когда вы работаете с delaunay и функциями delaunayn, присутствие копий может не иметь большого значения. Однако, поскольку многие запросы, обеспеченные классом delaunayTriangulation, являются базирующимся индексом, важно понять, что delaunayTriangulation триангулирует и работает с уникальным набором данных. Поэтому индексация на основе уникального набора точки является соглашением. Это данные сохраняется свойством Points delaunayTriangulation.
Следующий пример иллюстрирует важность ссылки на уникальный набор данных, сохраненный в свойстве Points при работе с delaunayTriangulation:
P = gallery('uniformdata',[25 2],0);
P(18,:) = P(8,:)
P(16,:) = P(6,:)
P(12,:) = P(2,:)
DT = delaunayTriangulation(P)
Points показывает, что дублирующиеся точки были удалены из данных.DT =
delaunayTriangulation with properties:
Points: [22x2 double]
ConnectivityList: [31x3 double]
Constraints: []DT.Points 'points'. Поэтому используйте следующий код, чтобы вычислить и построить график выпуклой оболочки:K = DT.convexHull(); plot(DT.Points(:,1),DT.Points(:,2),'.'); hold on plot(DT.Points(K,1),DT.Points(K,2),'-r');
delaunayTriangulation, то результат был бы неправильным. delaunayTriangulation работает с индексами, которые основаны на уникальном наборе данных DT.Points 'points'. Например, следующее произвело бы неправильный график, потому что K индексируется относительно DT.Points и не P:K = DT.convexHull(); plot(P(:,1),P(:,2),'.'); hold on plot(P(K,1),P(K,2),'-r');
delaunayTriangulation. Выполнение этого устраняет потенциал для беспорядка. Это может быть выполнено с помощью функции unique можно следующим образом: P = gallery('uniformdata',[25 2],0); P(18,:) = P(8,:) P(16,:) = P(6,:) P(12,:) = P(2,:) [~, I, ~] = unique(P,'first','rows'); I = sort(I); P = P(I,:); DT = delaunayTriangulation(P) % The point set is unique