Дифференциальные уравнения с частными производными

Функциональные сводные данные

Решатель УЧП
Функция помощника УЧП

Решатель УЧП

Это - решатель ^{MATLAB® PDE}.

Решатель Начальной Краевой задачи УЧП	Описание
`pdepe`	Решите начальные краевые задачи для систем параболических и эллиптических УЧП в одной пространственной переменной и время.

Функция помощника УЧП

Функция помощника УЧП	Описание
`pdeval`	Оцените числовое решение УЧП с помощью вывода `pdepe`.

Задачи с начальными значениями

pdepe решает системы параболических и эллиптических УЧП в одной пространственной переменной x и время t формы

c (x, t, u, \frac{}{∂u∂x}) \frac{}{}^{∂u∂t=x−m} \frac{}{\partial\partial x} (^{} xmf (x, t, u, \frac{}{∂u∂x})) +s (x, t, u, \frac{}{∂u∂x}) .

(1)

УЧП содержат для t0 ≤ t ≤ tf и ≤ x ≤ b. Интервал [a, b] должен быть конечным. m может быть 0, 1, или 2, соответствуя плите, цилиндрической, или сферической симметрии, соответственно. Если m> 0, то ≥ 0 должен также содержать.

В Уравнении 1, f (x, t, u, ∂u / ∂ x) термин потока, и s (x, t, u, ∂u / ∂ x) является характеристиками выброса. Термин потока должен зависеть от ∂u / ∂ x. Связь частных производных относительно времени ограничивается умножением диагональной матрицей c (x, t, u, ∂u / ∂ x). Диагональные элементы этой матрицы являются или тождественно нулем или положительный. Элемент, который является тождественно нулевым, соответствует эллиптическому уравнению и в противном случае к параболическому уравнению. Должно быть по крайней мере одно параболическое уравнение. Элемент c, который соответствует параболическому уравнению, может исчезнуть в изолированных значениях x, если они - точки mesh. Разрывы в c и/или s из-за материальных интерфейсов разрешены при условии, что точка mesh помещается в каждый интерфейс.

В начальное время t = t0, для всего x компоненты решения удовлетворяют начальные условия формы

u (x,_{t0})_{=u0} (x) .

(2)

На контуре x = a или x = b, для всего t компоненты решения удовлетворяют граничное условие формы

p (x, t, u) +q (x, t) f (x, t, u, \frac{}{∂u∂x}) =0.

(3)

q (x, t) диагональная матрица с элементами, которые являются или тождественно нулем или никогда не обнуляют. Обратите внимание на то, что граничные условия выражаются с точки зрения f, а не частной производной u относительно x ∂u / ∂ x. Кроме того, этих двух коэффициентов только p может зависеть от u.

Решатель УЧП

Решатель УЧП MATLAB, pdepe, решает начальные краевые задачи для систем параболических и эллиптических УЧП в одной пространственной переменной x и время t. В системе должно быть по крайней мере одно параболическое уравнение.

Решатель pdepe преобразовывает УЧП в ОДУ с помощью точной пространственной дискретизации второго порядка на основе фиксированного набора заданных пользователями узлов. Метод дискретизации описан в [1]. Интегрирование времени сделано с ode15s. Решатель pdepe использует возможности ode15s для решения дифференциально-алгебраических уравнений, которые возникают, когда Уравнение 1 содержит эллиптические уравнения, и для обработки Якобианов с заданным шаблоном разреженности. ode15s изменяет и временной шаг и формулу динамически.

После дискретизации эллиптические уравнения дают начало алгебраическим уравнениям. Если элементы вектора начальных условий, которые соответствуют эллиптическим уравнениям, не “сопоставимы” с дискретизацией, pdepe пытается настроить их прежде, чем начать интегрирование времени. Поэтому решение, возвращенное в течение начального времени, может иметь ошибку дискретизации, сопоставимую с этим в любое другое время. Если mesh прекрасна достаточно, pdepe может найти сопоставимые начальные условия близко к данным единицам. Если pdepe отображает сообщение, что он испытывает затруднения при нахождении сопоставимых начальных условий, попытайтесь совершенствовать mesh. Никакая корректировка не необходима для элементов вектора начальных условий, которые соответствуют параболическим уравнениям.

Синтаксис решателя УЧП

Базовый синтаксис решателя:

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan)

Примечание

Данные соответствия к терминам, использованным в Задачах с начальными значениями.

Входные параметры

`m`	Задает симметрию проблемы. `m` может быть `0` = плита, `1` = цилиндрический, или `2` = сферический. Это соответствует m в Уравнении 1.
`pdefun`	Функция, которая задает компоненты УЧП. Это вычисляет условия c, f, и s в Уравнении 1, и имеет форму [c,f,s] = pdefun(x,t,u,dudx) где `x` и `t` являются скалярами, и `u` и `dudx` являются векторами, которые аппроксимируют решение u и его частную производную относительно x. `c`, `f` и `s` являются векторами - столбцами. `c` хранит диагональные элементы матрицы c.
`icfun`	Функция, которая оценивает начальные условия. Это имеет форму u = icfun(x) Когда названо аргументом `x`, `icfun` оценивает и возвращает начальные значения компонентов решения в `x` в векторе - столбце `u`.
`bcfun`	Функция, которая оценивает условия p и q граничных условий. Это имеет форму [pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t) где `ul` является приближенным решением на левом контуре`, xl = a` и `ur` являются приближенным решением на правильном контуре `xr = b`. `pl` и `ql` являются векторами - столбцами, соответствующими p и диагональю q, оцененного в `xl`. Точно так же `pr` и `qr` соответствуют `xr`. Когда m> 0 и = 0, ограниченность решения рядом x = 0 требует, чтобы f исчезли в = 0. `pdepe` налагает это граничное условие автоматически, и это игнорирует значения, возвращенные в `pl` и `ql`.
`xmesh`	Вектор [`x0`, `x1`..., `xn`] определение точек, в которых числовое решение требуют на каждое значение в `tspan`. `x0` и `xn` соответствуют a и b, соответственно. Приближение второго порядка к решению сделано на mesh, заданной в `xmesh`. Обычно лучше использовать близко расположенные точки mesh, где решение изменяется быстро. `pdepe` не выбирает mesh в x автоматически. Необходимо обеспечить соответствующую фиксированную mesh в `xmesh`. Стоимость зависит строго от длины `xmesh`. Когда m> 0, не необходимо использовать мелкую сетку рядом x = 0, чтобы составлять координатную особенность. Элементы `xmesh` должны удовлетворить `x0` < `x1` < ... < `xn`. Длиной `xmesh` должен быть ≥ `3`.
`tspan`	Вектор [`t0`, `t1`..., `tf`] определение точек, в которых решение требуют на каждое значение в `xmesh`. `t0` и `tf` соответствуют t0 и tf, соответственно. `pdepe` выполняет интегрирование времени с решателем ОДУ, который выбирает и временной шаг и формулу динамически. Решения в точках, заданных в `tspan`, получены с помощью естественного непрерывного расширения формул интегрирования. Элементы `tspan` просто задают, где вы хотите ответы, и стоимость зависит слабо от длины `tspan`. Элементы `tspan` должны удовлетворить `t0` < `t1` < ... < `tf`. Длиной `tspan` должен быть ≥ `3`.

Выходным аргументом sol является трехмерный массив, такой что

sol (:, :, k) аппроксимирует компонент k решения u.
sol (i, :, k) аппроксимирует компонент k решения во время, которое tspan (i) и mesh указывает xmesh(:).
sol (i,j,k) аппроксимирует компонент k решения во время, которое tspan (i) и mesh указывает xmesh(j).

Опции решателя УЧП

Для большего количества усовершенствованных приложений можно также задать как опции решателя входных параметров и дополнительные параметры, которые передаются функциям УЧП.

опции

Структура дополнительных параметров, которые изменяют свойства интегрирования по умолчанию. Это - седьмой входной параметр.

sol = pdepe(m,pdefun,icfun,bcfun,...
            xmesh,tspan,options)

См. Опции Интегратора для получения дополнительной информации.

Опции интегратора

Свойства интегрирования по умолчанию в решателе УЧП MATLAB выбраны, чтобы решить типичные проблемы. В некоторых случаях можно улучшить производительность решателя путем переопределения этих значений по умолчанию. Вы делаете это путем предоставления pdepe одни или несколько значений свойств в структуре опций.

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options)

Используйте odeset, чтобы создать структуру опций. Только те опции базового решателя ОДУ, показанного в следующей таблице, доступны для pdepe. Значения по умолчанию, полученные, бросая входной параметр options, являются обычно удовлетворительными.

PDE Properties

Категория свойств	PropertyName
Контроль ошибок	`RelTol`, `AbsTol`, `NormControl`
Неродной размер	`InitialStep`, `MaxStep`

Единственный УЧП

Решение уравнения
Оценка решения

Решение Уравнения. Этот пример иллюстрирует прямую формулировку, решение и графическое изображение решения единственного УЧП

$^{} \frac{}{π2∂u∂t} = \frac{\partial^{}}{^{2u∂x2}} .$

Это уравнение содержит через определенный интервал 0 ≤ x ≤ 1 в течение многих времен t ≥ 0. В t = 0, решение удовлетворяет начальное условие

$u (x, 0) =sinπx .$

В x = 0 и x = 1, решение удовлетворяет граничные условия

$\begin{array}{l} u (0, t) \\ ^{=0πe−t} + \frac{\partial}{u∂x} (1, t) =0. \end{array}$

Примечание

Файл, pdex1.m, содержит полный код для этого примера. Это содержит все необходимые функции, закодированные как локальные функции. Чтобы видеть код в редакторе, введите edit pdex1 в командной строке. Чтобы запустить его, введите pdex1 в командной строке. Смотрите Синтаксис Решателя УЧП для получения дополнительной информации.

Перепишите УЧП. Напишите УЧП в форме
$c (x, t, u, \frac{}{∂u∂x}) \frac{}{}^{∂u∂t=x−m} \frac{}{\partial\partial x} (^{} xmf (x, t, u, \frac{}{∂u∂x})) +s (x, t, u, \frac{}{∂u∂x}) .$
Это - форма, показанная в Уравнении 1 и ожидаемый pdepe. Смотрите Задачи с начальными значениями для получения дополнительной информации. Для этого примера получившееся уравнение
$^{} \frac{}{}^{} \frac{}{π2ut=x0 x}^{} \frac{}{} (x0\partialu\partialx) +0$
с параметром m = 0 и условия
$\begin{array}{l} c (x, t, u, \frac{}{∂u∂x}) =^{} \\ π2f (x, t, u, \frac{}{∂u∂x}) = \frac{}{} \\ ∂u∂xs (x, t, u, \frac{}{∂u∂x}) =0. \end{array}$
Закодируйте УЧП. Если вы переписываете УЧП в форме, показанной выше (Уравнение 1), и идентифицируете условия, можно закодировать УЧП в функции, которую может использовать pdepe. Функция должна иметь форму
```
[c,f,s] = pdefun(x,t,u,dudx)
```
где c, f и s соответствуют c, f, и условиям s. Код ниже вычисляет c, f и s для проблемы в качестве примера.
```
function [c,f,s] = pdex1pde(x,t,u,DuDx)
c = pi^2;
f = DuDx;
s = 0;
```
Закодируйте функцию начальных условий. Необходимо закодировать начальные условия в функции формы
```
u = icfun(x)
```
Код ниже представляет начальные условия в функциональном pdex1ic.
```
function u0 = pdex1ic(x)
u0 = sin(pi*x);
```
Закодируйте функцию граничных условий. Необходимо также закодировать граничные условия в функции формы
```
[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
```
Граничные условия, написанные в той же форме как Уравнение 3,
$u (0, t) +0 \frac{\cdot\partial}{u∂x} (0, t) =0 в x=0$
и
$^{} πe−t+1 \frac{\cdot\partial}{u∂x} (1, t) =0 в x=1.$
Код ниже оценивает компоненты p (x, t, u) и q (x, t) граничных условий в функциональном pdex1bc.
```
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
pl = ul;
ql = 0;
pr = pi * exp(-t);
qr = 1;
```
В функциональном pdex1bc pl и ql соответствуют левым граничным условиям (x = 0), и pr и qr соответствуют правильному граничному условию (x = 1).
Выберите точки mesh для решения. Прежде чем вы будете использовать решатель УЧП MATLAB, необходимо задать точки mesh (t, x), в котором вы хотите, чтобы pdepe оценил решение. Задайте точки как векторы t и x.
t векторов и x играют различные роли в решателе (см. Решатель УЧП). В частности, стоимость и точность решения зависят строго от длины векторного x. Однако вычисление намного менее чувствительно к значениям в векторном t.
Этот пример запрашивает решение на mesh, произведенной 20 равномерно распределенными точками из пространственного интервала [0,1] и пять значений t от временного интервала [0,2].
```
x = linspace(0,1,20);
t = linspace(0,2,5);
```
Примените решатель УЧП. Пример вызывает pdepe с m = 0, функции pdex1pde, pdex1ic, и pdex1bc и mesh, заданная x и t, в котором pdepe должен оценить решение. Функция pdepe возвращает числовое решение в трехмерном массиве sol, где sol(i,j,k) аппроксимирует k th компонент решения, Великобритания, оцененная в t(i) и x(j).
```
m = 0;
sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
```
Этот пример использует @, чтобы передать pdex1pde, pdex1ic и pdex1bc как указатели на функцию к pdepe.
Примечание
См. Указатели на функции для получения дополнительной информации об указателях на функцию.
Просмотрите результаты. Завершите пример путем отображения результатов:
1. Извлеките и отобразите первый компонент решения. В этом примере решение u имеет только один компонент, но в иллюстративных целях, пример “извлекает” его от трехмерного массива. Объемная поверхностная диаграмма показывает поведение решения.
```
    u = sol(:,:,1);
    
    surf(x,t,u)    
    title('Numerical solution computed with 20 mesh points')
    xlabel('Distance x')
    ylabel('Time t')
```
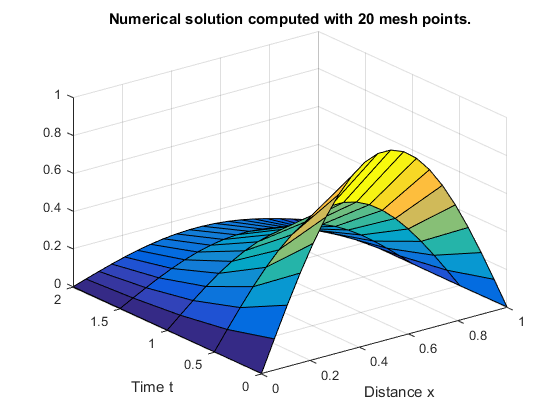
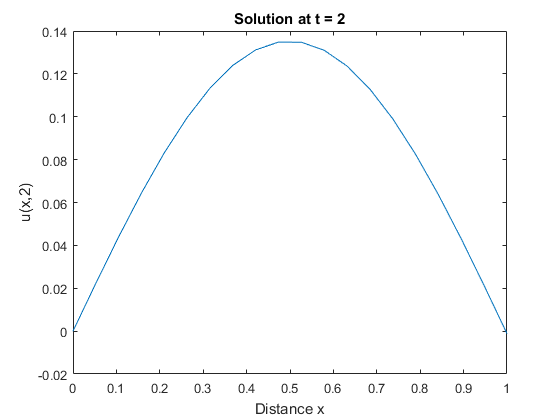
2. Отобразите профиль решений в tf, окончательном значении t. В этом примере, tf = t = 2.
```
    figure
    plot(x,u(end,:))
    title('Solution at t = 2')
    xlabel('Distance x')
    ylabel('u(x,2)')
```

Оценка Решения. После получения и графического изображения решения выше, вы можете интересоваться профилем решений для особого значения t или изменений времени решения в конкретной точке x. k th столбец u(:,k) (решения, извлеченного на шаге 7), содержит историю времени решения в x(k). j th строка u(j,:) содержит профиль решений в t(j).

Используя векторы x и u(j,:) и помощник функционируют pdeval, можно оценить решение u и его производная ∂u / ∂ x в любом наборе точек xout

[uout,DuoutDx] = pdeval(m,x,u(j,:),xout)

Пример pdex3 использует pdeval, чтобы оценить производную решения в xout = 0. Смотрите pdeval для деталей.

Система УЧП

Этот пример иллюстрирует решение системы дифференциальных уравнений с частными производными. Проблема взята от электродинамики. Это имеет пограничные слои в обоих концах интервала, и решение изменяется быстро для маленького t.

УЧП

$\begin{array}{l} \frac{_{}}{} \frac{^{}_{}}{^{}}_{}_{} \partialu1\partialt=0.024\partial2u1\partialx2-F(u1-u2) \\ \frac{_{}}{} \frac{^{}_{}}{^{}} ∂u2∂t=0.170∂2u2∂x2+F_{}_{} (u1-u2) \end{array}$

где F (y) = exp (5,73 лет) – exp (–11.46y). Уравнения содержат через определенный интервал 0 ≤ x ≤ 1 в течение многих времен t ≥ 0.

Решение u удовлетворяет начальные условия

$\begin{array}{l} _{u1} (x, 0) \\ _{≡1u2} (x, 0) ≡0 \end{array}$

и граничные условия

$\begin{array}{l} \frac{_{}}{∂u1∂x} (0, t) \\ _{≡0u2} (0, t) \\ _{≡0u1} (1, t) \\ \frac{_{}}{≡1∂u2∂x} (1, t) ≡0. \end{array}$

Примечание

Файл, pdex4.m, содержит полный код для этого примера. Это содержит все необходимые функции, закодированные как локальные функции. Чтобы видеть код в редакторе, введите edit pdex4 в командной строке. Чтобы запустить его, введите pdex4 в командной строке.

Перепишите УЧП. В форме, ожидаемой pdepe, уравнения
$\begin{matrix} \end{matrix} [11] \frac{}{\cdot*\partial\partial t} \begin{matrix} _{} \\ _{} \end{matrix} [u1u2] = \frac{}{\partial\partial x} [\begin{matrix} 0.024 (_{∂u1} / \partial x) \\ 0.170 (_{∂u2} / \partial x) \end{matrix}] + [\begin{matrix} −F_{}_{} (u1-u2) \\ F_{}_{} (u1-u2) \end{matrix}] .$
Граничные условия на частных производных вас должны быть записаны с точки зрения потока. В форме, ожидаемой pdepe, левое граничное условие
$\begin{matrix} _{} \end{matrix} [0u2] + \begin{matrix} \end{matrix} [10] \cdot* [\begin{matrix} 0.024 (_{∂u1} / \partial x) \\ 0.170 (_{∂u2} / \partial x) \end{matrix}] = \begin{matrix} \end{matrix} [00]$
и правильное граничное условие
$\begin{matrix} _{} \end{matrix} [u1-10] + \begin{matrix} \end{matrix} [01] \cdot* [\begin{matrix} 0.024 (_{∂u1} / \partial x) \\ 0.170 (_{∂u2} / \partial x) \end{matrix}] = \begin{matrix} \end{matrix} [00] .$
Закодируйте УЧП. После того, как вы переписываете УЧП в форме, показанной выше, можно закодировать его как функцию, которую может использовать pdepe. Функция должна иметь форму
```
[c,f,s] = pdefun(x,t,u,dudx)
```
где c, f и s соответствуют c, f, и условиям s в Уравнении 1.
```
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1]; 
f = [0.024; 0.17] .* DuDx; 
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];  
```
Закодируйте функцию начальных условий. Функция начальных условий должна иметь форму
```
u = icfun(x)
```
Код ниже представляет начальные условия в функциональном pdex4ic.
```
function u0 = pdex4ic(x);
u0 = [1; 0]; 
```
Закодируйте функцию граничных условий. Функции граничных условий должны иметь форму
```
[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
```
Код ниже оценивает компоненты p (x, t, u) и q (x, t) (Уравнение 3) граничных условий в функциональном pdex4bc.
```
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = [0; ul(2)]; 
ql = [1; 0];     
pr = [ur(1)-1; 0]; 
qr = [0; 1];     
```
Выберите точки mesh для решения. Решение изменяется быстро для маленького t. Программа выбирает размер шага вовремя, чтобы разрешить это резкое изменение, но видеть, что это поведение в графиках, чтобы вывести времена должно быть выбрано соответственно. Существуют пограничные слои в решении в обоих концах [0,1], таким образом, точки mesh должны быть помещены туда, чтобы разрешить эти резкие изменения. Часто некоторое экспериментирование необходимо, чтобы выбрать mesh, которая показывает поведение решения.
```
x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];
```
Примените решатель УЧП. Пример вызывает pdepe с m = 0, функции pdex4pde, pdex4ic, и pdex4bc и mesh, заданная x и t, в котором pdepe должен оценить решение. Функция pdepe возвращает числовое решение в трехмерном массиве sol, где sol(i,j,k) аппроксимирует k th компонент решения, μk, оцененный в t(i) и x(j).
```
m = 0;
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
```

Просмотрите результаты. Объемные поверхностные диаграммы показывают поведение компонентов решения.

u1 = sol(:,:,1);
u2 = sol(:,:,2);

figure
surf(x,t,u1)
title('u1(x,t)')
xlabel('Distance x')
ylabel('Time t')

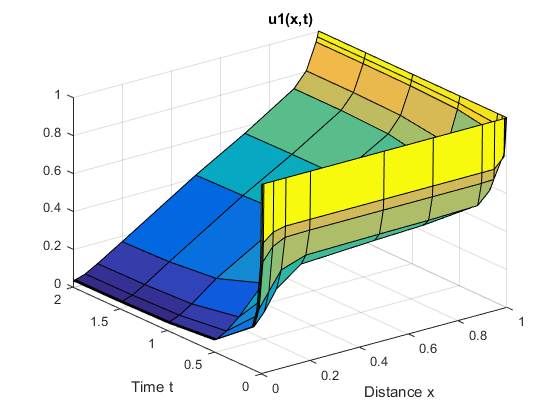
figure
surf(x,t,u2)
title('u2(x,t)')
xlabel('Distance x')
ylabel('Time t')

Дополнительные примеры

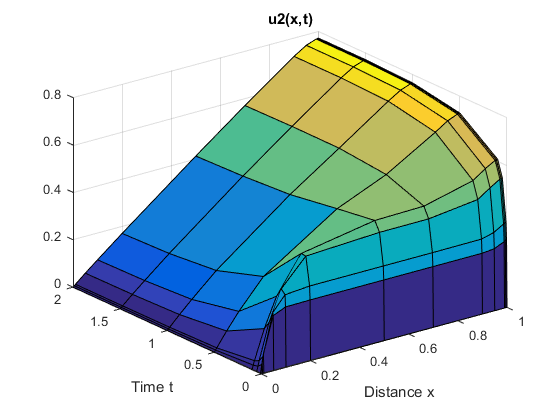
Следующие дополнительные примеры доступны. Ввод

edit examplename

просмотреть код и

examplename

запускать пример.

Имя в качестве примера	Описание
`pdex1`	Простой УЧП, который иллюстрирует прямую формулировку, вычисление и графическое изображение решения
`pdex2`	Проблема, которая включает разрывы
`pdex3`	Проблема, которая требует вычислительных значений частной производной
`pdex4`	Система двух УЧП, решение которых имеет пограничные слои и в концах интервала и изменяется быстро для маленького t.
`pdex5`	Система УЧП со ступенчатыми функциями как начальные условия

Ссылки

[1] Skeel, R. D. и М. Берзиньш, "Метод для Пространственной Дискретизации Параболических Уравнений в Одной Пространственной переменной", SIAM Journal на Научном и Статистическом Вычислении, Издании 11, 1990, стр 1-32.

Смотрите также

bvp4c | bvp5c | ode45 | pdepe

Была ли эта тема полезной?

Документация