graphtraverse

Пересеките график следующими смежными узлами

Синтаксис

[disc, pred, closed] = graphtraverse(G, S) [...] = graphtraverse(G, S, ...'Depth', DepthValue, ...) [...] = graphtraverse(G, S, ...'Directed', DirectedValue, ...) [...] = graphtraverse(G, S, ...'Method', MethodValue, ...)

Аргументы

`G`	N на n разреженная матрица, которая представляет ориентированного графа. Ненулевые записи в матричном `G` указывают на присутствие ребра.
`S`	Целое число, которое указывает на исходный узел в графике `G`.
`DepthValue`	Целое число, которое указывает на узел в графике `G`, который задает глубину поиска. Значением по умолчанию является `Inf` (бесконечность).
`DirectedValue`	Свойство, которое указывает, направлен ли график `G` или неориентированный. Введите `false` для неориентированного графа. Это приводит к верхнему треугольнику проигнорированной разреженной матрицы. Значением по умолчанию является `true`.
`MethodValue`	Вектор символов или строка, которая задает алгоритм, раньше пересекали график. Выбор: `'BFS'` — Поиск в ширину. Временной сложностью является `O(N+E)`, где `N` и `E` являются количеством узлов и ребер соответственно. `'DFS'` — Алгоритм по умолчанию. Поиск в глубину. Временной сложностью является `O(N+E)`, где `N` и `E` являются количеством узлов и ребер соответственно.

Описание

Совет

Дополнительные сведения о функциях теории графов см. в Функциях Теории графов.

[disc, pred, closed] = graphtraverse(G, S) график пересечений G, начинающий с узла, обозначается целочисленным S. G является N на n разреженной матрицей, которая представляет ориентированного графа. Ненулевые записи в матричном G указывают на присутствие ребра. disc является вектором индексов узла в порядке, в котором они обнаружены. pred является вектором индексов узла-предшественников (перечисленный в порядке индексов узла) получившегося дерева охвата. closed является вектором индексов узла в порядке, в котором они закрываются.

[...] = graphtraverse(G, S, ...'PropertyName', PropertyValue, ...) вызывает graphtraverse с дополнительными свойствами, которые используют имя свойства / пары значения свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должен быть заключен в одинарные кавычки и нечувствительный к регистру. Это имя свойства / пары значения свойства следующие:

[...] = graphtraverse(G, S, ...'Depth', DepthValue, ...) задает глубину поиска. DepthValue является целым числом, указывающим на узел в графике G. Значением по умолчанию является Inf (бесконечность).

[...] = graphtraverse(G, S, ...'Directed', DirectedValue, ...) указывает, направлен ли график или неориентированный. Установите DirectedValue на false для неориентированного графа. Это приводит к верхнему треугольнику проигнорированной разреженной матрицы. Значением по умолчанию является true.

[...] = graphtraverse(G, S, ...'Method', MethodValue, ...) позволяет вам указать, что алгоритм раньше пересекал график. Выбор:

'BFS' — Поиск в ширину. Временной сложностью является O(N+E), где N и E являются количеством узлов и ребер соответственно.
'DFS' — Алгоритм по умолчанию. Поиск в глубину. Временной сложностью является O(N+E), где N и E являются количеством узлов и ребер соответственно.

Примеры

Создайте ориентированного графа с 10 узлами и 12 ребрами.

DG = sparse([1 2 3 4 5 5 5 6 7 8 8 9],...
              [2 4 1 5 3 6 7 9 8 1 10 2],true,10,10)

DG =

   (3,1)        1
   (8,1)        1
   (1,2)        1
   (9,2)        1
   (5,3)        1
   (2,4)        1
   (4,5)        1
   (5,6)        1
   (5,7)        1
   (7,8)        1
   (6,9)        1
   (8,10)       1

h = view(biograph(DG))
Biograph object with 10 nodes and 12 edges.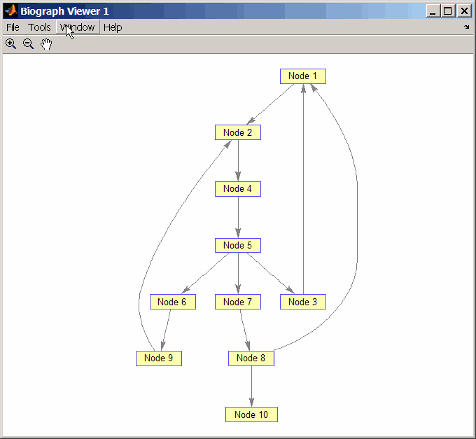

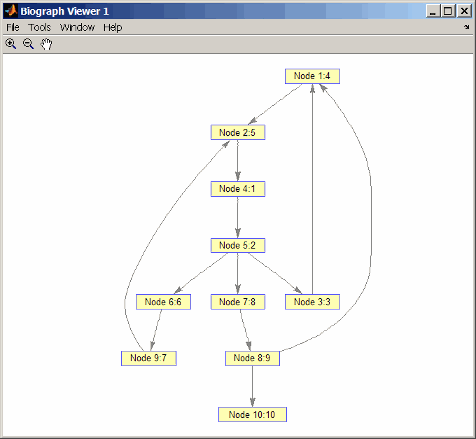
Пересеките график, чтобы найти порядок открытия поиска в глубину (DFS), запускающийся в узле 4.
```
order = graphtraverse(DG,4)

order =

     4     5     3     1     2     6     9     7     8    10
```

Маркируйте узлы порядком открытия DFS.

for i = 1:10
    h.Nodes(order(i)).Label =...
			sprintf('%s:%d',h.Nodes(order(i)).ID,i);
end
h.ShowTextInNodes = 'label'
dolayout(h)

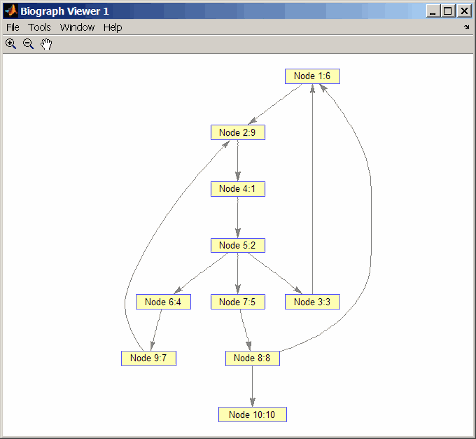
Пересеките график, чтобы найти порядок открытия поиска в ширину (BFS), запускающийся в узле 4.
```
order = graphtraverse(DG,4,'Method','BFS')

order =

     4     5     3     6     7     1     9     8     2    10
```

Маркируйте узлы порядком открытия BFS.

for i = 1:10
    h.Nodes(order(i)).Label =...
			sprintf('%s:%d',h.Nodes(order(i)).ID,i);
end
h.ShowTextInNodes = 'label'
dolayout(h)

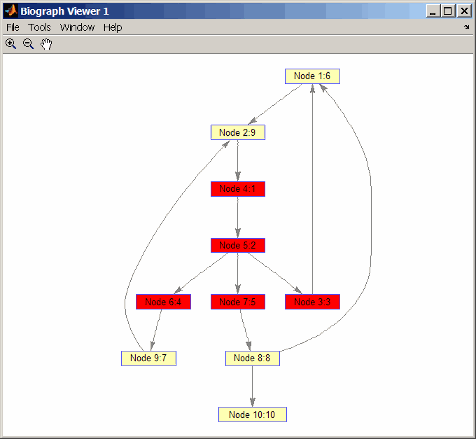
Найдите и окрасьте узлы, которые являются близко к (в двух ребрах) узел 4.
```
node_idxs = graphtraverse(DG,4,'depth',2)

node_idxs =

     4     5     3     6     7

set(h.nodes(node_idxs),'Color',[1 0 0])
```

Ссылки

[1] Sedgewick, R., (2002). Алгоритмы на C++, алгоритмы графика части 5 (Аддисон-Уэсли).

[2] Siek, J.G., Ли, L-Q и Lumsdaine, A. (2002). Руководство пользователя библиотеки графика повышения и справочник, (верхний Сэддл-Ривер, образование НДЖ:ПИРСОНА).

Документация

graphtraverse

Синтаксис

Аргументы

Описание

Совет

Примеры

Ссылки

Смотрите также

Представленный в R2006b

Документация Bioinformatics Toolbox

Поддержка