Адаптивные структуры эквалайзера обеспечивают субоптимальную коррекцию изменений времени в характеристиках канала распространения, но привлекательны, потому что их вычислительная сложность ниже, чем Эквалайзеры MLSE.
В Communications Toolbox™, comm.LinearEqualizer и Системных объектах comm.DecisionFeedbackEqualizer и Линейном Эквалайзере Обратной связи Эквалайзера и Решения блокирует сетевые фильтры задержки касания использования, чтобы компенсировать линейно модулируемый сигнал через дисперсионный канал. Эти функции выводят оценку сигнала, с помощью оценки канала, смоделированного как фильтр конечного входного ответа (FIR).
Декодирование полученного сигнала использует эти шаги:
Примените КИХ-фильтр, соответствуя оценке канала, к символам во входном сигнале.
Оценка сигнала выводится и также используется, чтобы обновить веса касания для следующего символа. Оценка сигнала и обновление весов зависят от адаптивной структуры эквалайзера и алгоритма.
Адаптивные опции структуры эквалайзера линейны или обратная связь решения. Адаптивные опции алгоритма являются наименьшее количество среднего квадратичного (LMS), рекурсивным средним квадратичным (RMS) или постоянным алгоритмом модуля (CMA). Для справочного материала об адаптивных эквалайзерах смотрите работы, перечисленные в Выбранной Библиографии для Эквалайзеров.
Можно сконфигурировать эквалайзер, чтобы действовать в качестве расположенного с интервалами символом эквалайзера или в качестве дробного расположенного с интервалами символом эквалайзера.
Чтобы управлять эквалайзером на расположенном с интервалами символом уровне, задайте количество выборок на символ как 1. Эквалайзеры уровня символа имеют касания, расположенные с интервалами в длительности символа. Эквалайзеры уровня символа чувствительны к синхронизации фазы.
Чтобы управлять эквалайзером на дробном расположенном с интервалами символом уровне, задайте количество входных выборок на символ как целое число, больше, чем 1, и обеспечьте входной сигнал, сверхдискретизированный на том уровне выборки. Дробные расположенные с интервалами символом эквалайзеры имеют касания, расположенные с интервалами в целочисленной части длительности вводимого символа. Дробные расположенные с интервалами символом эквалайзеры не чувствительны к синхронизации фазы.
Эквалайзер MLSE поддерживает дробный интервал символа, но использование его не рекомендуется. Вычислительная сложность MLSE и нагрузка растут экспоненциально с длиной дисперсии времени канала. Сверхдискретизация входа означала бы умножать экспоненциальный термин на количество выборок на символ.
Линейные эквалайзеры могут удалить интерференцию межсимвола (ISI), когда частотная характеристика канала не имеет никакого пустого указателя. Если пустой указатель существует в частотной характеристике канала, линейные эквалайзеры имеют тенденцию улучшать шум. В этом случае используйте эквалайзеры обратной связи решения, чтобы не улучшать шум.
Линейный эквалайзер состоит из коснувшейся строки задержки, которая хранит выборки от входного сигнала. Однажды на период символа, эквалайзер выводит взвешенную сумму значений в строке задержки и обновляет веса, чтобы подготовиться к следующему периоду символа.
Линейные эквалайзеры могут быть расположены с интервалами символом или дробные расположенный с интервалами символом.
Для расположенного с интервалами символом эквалайзера количество выборок на символ, K, равняется 1. Выходная частота дискретизации равняется входной частоте дискретизации.
Для дробного расположенного с интервалами символом эквалайзера количество выборок на символ, K, является целым числом, больше, чем 1. Как правило, K 4 для незначительно расположенных с интервалами эквалайзеров. Выходная частота дискретизации является 1/T, и входной частотой дискретизации является K/T, где T является периодом символа. Обновление веса касания происходит при норме выработки.
Это схематические показы линейный эквалайзер с весами L, периодом символа T и выборками K на символ. Если K равняется 1, результатом является расположенный с интервалами символом линейный эквалайзер вместо дробного расположенного с интервалами символом линейного эквалайзера.
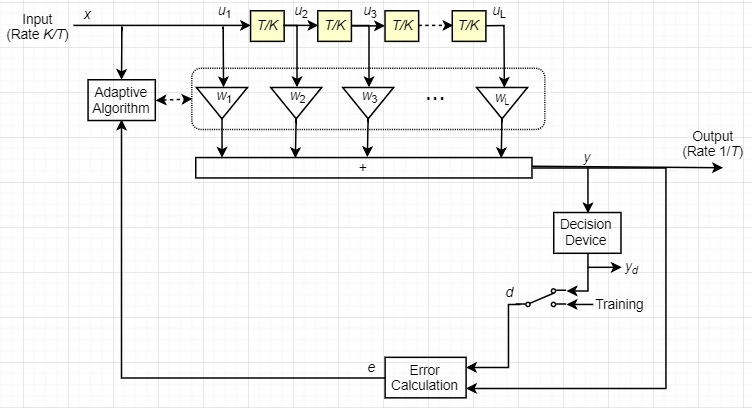
В каждый период символа эквалайзер получает выборки входа K в коснувшейся строке задержки. Эквалайзер затем выводит взвешенную сумму значений в коснувшейся строке задержки и обновляет веса, чтобы подготовиться к следующему периоду символа.
Эквалайзер обратной связи решения (DFE) является нелинейным эквалайзером, который уменьшает интерференцию межсимвола (ISI) в выборочных частотой каналах. Если пустой указатель существует в частотной характеристике канала, DFEs не улучшают шум. DFE состоит из коснувшейся строки задержки, которая хранит выборки от входного сигнала и содержит прямой фильтр и фильтр обратной связи. Прямой фильтр подобен линейному эквалайзеру, в то время как фильтр обратной связи содержит коснувшуюся строку задержки, входные параметры которой являются решениями, принятыми о компенсируемом сигнале. Однажды на период символа, эквалайзер выводит взвешенную сумму значений в строке задержки и обновляет веса, чтобы подготовиться к следующему периоду символа.
DFEs может быть расположен с интервалами символом или дробный расположенный с интервалами символом.
Для расположенного с интервалами символом эквалайзера количество выборок на символ, K, равняется 1. Выходная частота дискретизации равняется входной частоте дискретизации.
Для дробного расположенного с интервалами символом эквалайзера количество выборок на символ, K, является целым числом, больше, чем 1. Как правило, K 4 для дробных расположенных с интервалами символом эквалайзеров. Выходная частота дискретизации является 1/T, и входной частотой дискретизации является K/T. Коснитесь обновление веса происходит при норме выработки.
Это схематические показы дробный расположенный с интервалами символом DFE в общей сложности с весами N, периодом символа T и выборками K на символ. Фильтр имеет L прямые веса и N-L веса обратной связи. Прямой фильтр наверху, и фильтр обратной связи в нижней части. Если K равняется 1, результатом является расположенный с интервалами символом DFE вместо дробного расположенного с интервалами символом DFE.
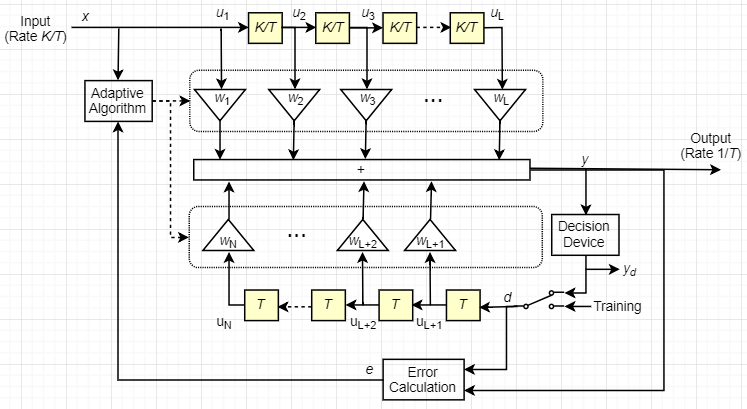
В каждый период символа эквалайзер получает выборки входа K в прямом фильтре, а также одно решение или учебную выборку в фильтре обратной связи. Эквалайзер затем выводит взвешенную сумму значений в форварде и строках задержки обратной связи и обновляет веса, чтобы подготовиться к следующему периоду символа.
Алгоритм для блока Adaptive Algorithm в схематическом совместно оптимизирует веса обратной связи и форвард. Объединенная оптимизация особенно важна для алгоритма RLS.
В типовых приложениях эквалайзер начинает в учебном режиме собирать информацию о канале и более поздние переключатели к направленному на решение режиму.
Когда эквалайзер действует в учебном режиме, ссылочный сигнал является предварительной установкой известная переданная последовательность.
Когда эквалайзер действует в направленном на решение режиме, ссылочный сигнал является обнаруженной версией выходного сигнала, обозначенного y d в схематическом.
Алгоритм CMA не имеет никакого учебного режима. Учебный режим только применяется при использовании LMS или алгоритма RLS.
Ошибочная операция вычисления производит сигнал, данный этим выражением, где R является константой, связанной с сигнальным созвездием.
Для линейного и структур эквалайзера обратной связи решения, выбор LMS, RLS или CMA определяет алгоритмы, используемые, чтобы установить веса касания и выполнить ошибочное вычисление. Новый набор весов касания зависит от
Текущий набор весов касания
Входной сигнал
Выходной сигнал
Ссылочный сигнал, d, для LMS и адаптивных алгоритмов RLS только. Ссылочные характеристики сигнала зависят от рабочего режима эквалайзера.
Для LMS-алгоритма, относясь к предыдущему схематическому, w является вектором всех весов wi, и u является вектором всех входных параметров ui. На основе текущего набора весов LMS-алгоритм создает новый набор весов как
w, новый = w, текущий + (StepSize) u *e.
Размер шага, используемый адаптивным алгоритмом, задан как положительная скалярная величина. Увеличение размера шага уменьшает время сходимости эквалайзера, но заставляет компенсируемый выходной сигнал быть менее стабильным. Чтобы определить максимальный размер шага, позволенный при использовании адаптивного алгоритма LMS, используйте функцию объекта maxstep. Оператор * обозначает сопряженное комплексное число и ошибочное вычисление e = d - y.
Для алгоритма RLS, относясь к предыдущему схематическому, w является вектором всех весов wi, и u является вектором всех входных параметров ui. На основе текущего набора входных параметров, u, и матрицы обратной корреляции, P, алгоритм RLS сначала вычисляет вектор усиления Кальмана, K, как
Фактор упущения, используемый адаптивным алгоритмом, задан как скаляр в области значений (0, 1]. Уменьшение фактора упущения уменьшает время сходимости эквалайзера, но заставляет компенсируемый выходной сигнал быть менее стабильным. H обозначает, что Эрмитовы транспонируют. На основе текущей матрицы обратной корреляции новая матрица обратной корреляции
На основе текущего набора весов алгоритм RLS создает новый набор весов как
w, новый = w current+K*e.
Оператор * обозначает сопряженное комплексное число и ошибочное вычисление e = d - y.
Для CMA адаптивный алгоритм, относясь к предыдущему схематическому, w является вектором всех весов wi, и u является вектором всех входных параметров ui. На основе текущего набора весов CMA адаптивный алгоритм создает новый набор весов как
w, новый = w, текущий + (StepSize) u *e.
Размер шага, используемый адаптивным алгоритмом, задан как положительная скалярная величина. Увеличение размера шага уменьшает время сходимости эквалайзера, но заставляет компенсируемый выходной сигнал быть менее стабильным. Чтобы определить максимальный размер шага, позволенный CMA адаптивный алгоритм, используйте функцию объекта maxstep. Оператор * обозначает сопряженное комплексное число и ошибочное вычисление e = y (R - |y|2), где R является константой, связанной с сигнальным созвездием.
Выберите линейное или структуру эквалайзера обратной связи решения. Решите который адаптивный алгоритм использовать — LMS, RLS или CMA. Задайте настройки для структуры и специфичных для алгоритма режимов работы.
Конфигурирование эквалайзера включает линейный выбор или структура обратной связи решения, выбор адаптивного алгоритма и определение структуры и алгоритма определенные режимы работы.
Лучший выбор адаптивного алгоритма зависит от вашей отдельной ситуации. Рассмотрите эти обобщения при решении, какой адаптивный алгоритм лучше всего соответствует потребностям:
LMS-алгоритм выполняется быстро, но медленно сходится, и его сложность растет линейно с количеством весов.
Алгоритм RLS сходится быстро, но его сложность растет с квадратом количества весов, примерно говоря. Этот алгоритм может также быть нестабильным, когда количество весов является большим.
Постоянный алгоритм модуля (CMA) полезен, когда никакой учебный сигнал не доступен, и работает лучше всего на постоянные модуляции модуля, такие как PSK.
Если CMA не имеет никакой дополнительной информации о стороне, он может ввести неоднозначность фазы. Например, веса, найденные CMA, могут произвести совершенную совокупность QPSK, но ввести вращение фазы 90, 180, или 270 градусов. В этом случае или используйте алгоритм исправления неоднозначности фазы или выберите дифференциальную схему модуляции, потому что дифференциальные схемы модуляции нечувствительны к неоднозначности фазы.
Чтобы просмотреть или изменить любые свойства адаптивного эквалайзера, используйте синтаксис, описанный для объектов канала в Отображении и Изменении Свойств объектов.
Для получения дополнительной информации об адаптивных алгоритмах, смотрите ссылки, перечисленные в Выбранной Библиографии для Эквалайзеров.
Чтобы создать адаптивный объект эквалайзера для использования в MATLAB®, выберите comm.LinearEqualizer или comm.DecisionFeedbackEqualizer System object™. Для Simulink® используйте блок Linear Equalizer или Decision Feedback Equalizer. На основе характеристик канала распространения в вашей симуляции используйте критерии в Коррекции, чтобы выбрать структуру эквалайзера.
Объект эквалайзера имеет многочисленные свойства, которые записывают информацию об эквалайзере. Свойства могут быть связаны с
Структура эквалайзера, такого как количество касаний.
Адаптивный алгоритм, который эквалайзер использует, такие как размер шага в алгоритме CMA или LMS.
Информация о текущем состоянии эквалайзера. Объект эквалайзера может вывести значения весов.
Чтобы просмотреть или изменить любые свойства объекта эквалайзера, используйте синтаксис, описанный для объектов канала в Отображении и Изменении Свойств объектов.
Определение объекта эквалайзера
Этот код создает объекты эквалайзера для трех настроек.
Расположенный с интервалами символом линейный эквалайзер RLS с 10 весами.
Незначительно расположенный с интервалами линейный эквалайзер RLS с 10 весами, совокупностью BPSK и двумя выборками на символ.
Обратная связь решения эквалайзер RLS с тремя весами в фильтре feedforward и двумя весами в фильтре обратной связи.
Все три объекта эквалайзера задают адаптивный алгоритм RLS с фактором упущения 0,3.
Создайте объекты эквалайзера различных типов. Отметьте настройки по умолчанию, используемые свойствами, которые не установлены с помощью пар 'Name,Value'.
eqlin = comm.LinearEqualizer('Algorithm','RLS','NumTaps',10,'ForgettingFactor',0.3)
eqlin =
comm.LinearEqualizer with properties:
Algorithm: 'RLS'
NumTaps: 10
ForgettingFactor: 0.3000
InitialInverseCorrelationMatrix: 0.1000
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eqfrac = comm.LinearEqualizer('Algorithm','RLS','NumTaps',10,'ForgettingFactor',0.3, ... 'Constellation',[-1 1],'InputSamplesPerSymbol',2)
eqfrac =
comm.LinearEqualizer with properties:
Algorithm: 'RLS'
NumTaps: 10
ForgettingFactor: 0.3000
InitialInverseCorrelationMatrix: 0.1000
Constellation: [-1 1]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 2
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eqdfe = comm.DecisionFeedbackEqualizer('Algorithm','RLS','NumForwardTaps',3, ... 'NumFeedbackTaps',2,'ForgettingFactor',0.3)
eqdfe =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'RLS'
NumForwardTaps: 3
NumFeedbackTaps: 2
ForgettingFactor: 0.3000
InitialInverseCorrelationMatrix: 0.1000
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Адаптивное присвоение алгоритма
Присвойте адаптивный алгоритм, используемый эквалайзером со свойством Algorithm. Сделайте присвоение с помощью Имени, пар Значения при создании объекта или со встроенным выражением после создания объекта.
Присвоение алгоритма
Присвойте адаптивный алгоритм при создании объекта эквалайзера.
eqlms = comm.LinearEqualizer('Algorithm','LMS');
Создайте эквалайзер, возражают и присваивают желаемый адаптивный алгоритм со встроенным выражением после создания объекта.
eqrls = comm.LinearEqualizer; eqrls.Algorithm
ans = 'LMS'
Когда eqrls создается, настройки свойства по умолчанию используются. LMS является адаптивным алгоритмом по умолчанию. Обновите eqrls, чтобы использовать адаптивный алгоритм RLS.
eqrls.Algorithm = 'RLS';
eqrls.Algorithmans = 'RLS'
Клонирование и дублирование объектов
Создайте адаптивный объект алгоритма путем клонирования существующего объекта эквалайзера, и затем изменения его свойств. Клонируйте eqlms, чтобы создать независимый эквалайзер, eqcma, затем обновите алгоритм к 'CMA'.
eqcma = clone(eqlms); eqcma.Algorithm
ans = 'LMS'
eqcma.Algorithm = 'CMA';
eqcma.Algorithmans = 'CMA'
Если вы хотите независимую копию, используйте команду clone вместо того, чтобы копировать объект с помощью равного оператора, c2 = c1.
eqlms.NumTaps
ans = 5
eq2 = eqlms; eq2.NumTaps = 6; eq2.NumTaps
ans = 6
eqlms.NumTaps
ans = 6
Команда clone создает копию eqlms, который независим от eqlms. В отличие от этого, команда, eqB = eqA создает eqB как ссылку на eqA, так, чтобы eqB и eqA всегда имели идентичные настройки свойства.
Линейно компенсируйте систему Используя различные планы подготовки
Линейно компенсируйте символы Используя основанное на EVM обучение
Линейно компенсируйте систему Используя различные планы подготовки
Продемонстрируйте, что линейная коррекция с помощью алгоритма наименьшее количество средних квадратичных (LMS), чтобы восстановить символы QPSK прошла через канал AWGN. Примените различные планы подготовки эквалайзера и покажите ошибочное значение символа.
Системный Setup
Моделируйте модулируемую QPSK систему, подвергающуюся AWGN. Передайте пакеты, состоявшие из 200 учебных символов и 1 800 случайных символов данных. Сконфигурируйте линейный эквалайзер LMS, чтобы восстановить пакетные данные.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',5,'ReferenceTap',3,'StepSize',0.01);
Обучите эквалайзер в начале каждого пакета со сбросом
Процесс каждый пакет с помощью предварительно ожидаемых учебных символов. Сбросьте эквалайзер после обработки каждого пакета. При сбросе эквалайзера после того, как каждый пакет обеспечивает эквалайзер, чтобы обучить касания без априорного знания. Графики сигнала ошибки эквалайзера для первого, второго, и последнего пакета показывают более высокие ошибки символа в начале каждого пакета.
jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); [~,err] = lineq(rx,trainingSymbols); reset(lineq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; jj = jj+1; end end

Обучите эквалайзер в начале каждого пакета без сброса
Процесс каждый пакет с помощью предварительно ожидаемых учебных символов. Не сбрасывайте эквалайзер после того, как каждый пакет будет обработан. Не сбрасывая после каждого пакета, эквалайзер сохраняет веса касания от учебных предшествующих пакетов. Графики сигнала ошибки эквалайзера для первого, второго, и последнего пакета показывают, что после начальной подготовки на первом пакете, последующие пакеты имеют меньше ошибок символа в начале каждого пакета.
release(lineq) jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; channel = 1; rx = awgn(packet*channel,SNR); [~,err] = lineq(rx,trainingSymbols); if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; jj = jj+1; end end

Обучайте эквалайзер периодически
Системы с сигналами, подвергающимися изменяющимся во времени каналам, требуют, чтобы периодическое обучение эквалайзера поддержать соединило изменения канала. Задайте систему, которая имеет 200 символов обучения каждым 1 800 символам данных. Между обучением эквалайзер не обновляет веса касания. Процессы эквалайзера 200 символов на пакет.
Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);Установите свойство AdaptAfterTraining на false останавливать обновления веса касания эквалайзера после учебной фазы.
release(lineq) lineq.AdaptAfterTraining = false
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 5
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: false
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Компенсируйте данные, которым повреждают. Постройте угловую погрешность от канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал отличается, эквалайзер, вывод не удаляет эффекты канала. Кроме того, выходная совокупность вращается из синхронизации, приводящей к битовым ошибкам.
[y,err] = lineq(rx,trainingSymbols); figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('Time (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(err)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel Without Retraining')

scatterplot(y)

Установите свойство TrainingInputPort на true конфигурировать эквалайзер, чтобы переобучить касания, когда сообщено входом trainFlag. Эквалайзер обучается только, когда trainFlag является true. После каждых 2 000 символов эквалайзер переобучает касания и сохраняет, соединяют изменения канала. Постройте угловую погрешность от канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал отличается, эквалайзер, вывод удаляет эффекты канала. Кроме того, выходная совокупность не вращается из синхронизации, и битовые ошибки уменьшаются.
release(lineq) lineq.TrainingFlagInputPort = true; symbolCnt = 0; numPackets = length(rx)/spp; trainFlag = true; trainingPeriod = 2000; eVec = zeros(size(rx)); yVec = zeros(size(rx)); for p=1:numPackets [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ... lineq(rx((p-1)*spp+1:p*spp,1),trainingSymbols,trainFlag); symbolCnt = symbolCnt + spp; if symbolCnt >= trainingPeriod trainFlag = true; symbolCnt = 0; else trainFlag = false; end end figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('t (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(eVec)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel With Retraining')

scatterplot(yVec)

Линейно компенсируйте символы Используя основанное на EVM обучение
Восстановите символы QPSK с линейным эквалайзером, с помощью постоянного алгоритма модуля (CMA) и основанного на EVM обучения касаний. При использовании слепых алгоритмов эквалайзера, таких как CMA, можно обучить касания эквалайзера с помощью свойства AdaptWeights запустить и остановить обучение. Используйте функции помощника, чтобы сгенерировать графики и применить исправление фазы.
Инициализируйте системные переменные.
rng(123456); M = 4; % QPSK numSymbols = 100; numPackets = 5000; raylChan = comm.RayleighChannel('PathDelays',[0 1], ... 'AveragePathGains',[0 -12],'MaximumDopplerShift',1e-5); SNR = 50; adaptWeights = true;
Создайте эквалайзер и Системные объекты EVM. Системный объект эквалайзера задает линейный эквалайзер с помощью CMA адаптивный алгоритм. Вызовите функцию помощника, чтобы инициализировать графики фигуры.
lineq = comm.LinearEqualizer('Algorithm','CMA', ... 'NumTaps',5,'ReferenceTap',3, ... 'StepSize',0.03,'AdaptWeightsSource','Input port')
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'CMA'
NumTaps: 5
StepSize: 0.0300
Constellation: [1x4 double]
ReferenceTap: 3
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Input port'
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
info(lineq)
ans = struct with fields:
Latency: 2
evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation'); [errPlot,evmPlot,scatSym,adaptState] = initFigures(numPackets,lineq);
Цикл коррекции
Выполните эти шаги, чтобы реализовать цикл коррекции.
Сгенерируйте пакеты данных о PSK.
Примените Релеевское замирание и AWGN к данным о передаче.
Примените коррекцию к полученным данным и исправление фазы к эквалайзеру вывод.
Оцените EVM и переключите флаг adaptWeights к true или false на основе уровня EVM.
Обновите графики фигуры.
for p=1:numPackets data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); rx = awgn(raylChan(tx),SNR); rxDelay = finddelay(rx,tx); [y,err,wts] = lineq(rx,adaptWeights); y = phaseCorrection(y); evmEst = evm(y); adaptWeights = (evmEst > 20); updateFigures(errPlot,evmPlot,scatSym,adaptState, ... wts,y(end),evmEst,adaptWeights,p,numPackets) end

rxDelay
rxDelay = 0
Графики фигуры показывают, что, когда EVM отличается, переключатели эквалайзера в и из направленного на решение режима адаптации веса.
Функции помощника
Эта функция помощника инициализирует фигуры, которые показывают квадратический график результатов симуляции.
function [errPlot,evmPlot,scatter,adaptState] = initFigures(numPkts,lineq) yVec = nan(numPkts,1); evmVec = nan(numPkts,1); wVec = zeros(lineq.NumTaps,1); adaptVec = nan(numPkts,1); figure subplot(2,2,1) evmPlot = stem(wVec); grid on; axis([1 lineq.NumTaps 0 1.8]) xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2) scatter = plot(yVec, '.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot'); subplot(2,2,3) adaptState = plot(adaptVec); grid on; axis([0 numPkts -0.2 1.2]) ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal') subplot(2,2,4) errPlot = plot(evmVec); grid on; axis([1 numPkts 0 100]) xlabel('Symbols'); ylabel('EVM (%)'); title('EVM') end
Эта функция помощника обновляет фигуры.
function updateFigures(errPlot,evmPlot,scatSym, ... adaptState,w,y,evmEst,adaptWts,p,numFrames) persistent yVec evmVec adaptVec if p == 1 yVec = nan(numFrames,1); evmVec = nan(numFrames,1); adaptVec = nan(numFrames,1); end yVec(p) = y; evmVec(p) = evmEst; adaptVec(p) = adaptWts; errPlot.YData = abs(evmVec); evmPlot.YData = abs(w); scatSym.XData = real(yVec); scatSym.YData = imag(yVec); adaptState.YData = adaptVec; drawnow limitrate end
Эта функция помощника применяет исправление фазы.
function y = phaseCorrection(y) a = angle(y((real(y) > 0) & (imag(y) > 0))); a(a < 0.1) = a(a < 0.1) + pi/2; theta = mean(a) - pi/4; y = y * exp(-1i*theta); end
Для соответствующей коррекции необходимо определить и объяснить системные задержки. Как показано в следующем примере, можно использовать функцию finddelay, чтобы определить системную задержку. Этот пример использует линейную коррекцию LMS, но тот же подход допустим для RLS и CMS адаптивные алгоритмы и для эквалайзеров обратной связи решения.
Линейно компенсируйте задержанный сигнал
Моделируйте систему с задержкой между переданными символами и полученными выборками. Типичные системы имеют фильтры передатчика и получателя, которые приводят к задержке. Эта задержка должна составляться, чтобы синхронизировать систему. В этом примере системная задержка введена без передачи, и получите фильтры. Линейная коррекция, с помощью алгоритма наименьшее количество средних квадратичных (LMS), восстанавливает символы QPSK.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;Сгенерируйте модулируемые QPSK символы. Примените многопутевую фильтрацию канала, системную задержку и AWGN к переданным символам.
data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); % OQPSK delayedSym = systemDelay(filter(mpChan,1,tx)); rx = awgn(delayedSym,snr,'measured');
Создайте эквалайзер и Системные объекты EVM. Системный объект эквалайзера задает линейный эквалайзер с помощью LMS-алгоритма.
lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',9,'ReferenceTap',5); evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation');
Компенсируйте, не настраивая входную задержку
Компенсируйте полученные символы.
[y1,err1,wts1] = lineq(rx,tx(1:numTrainingSymbols,1));
Найдите задержку между полученными символами и переданными символами при помощи функции finddelay.
rxDelay = finddelay(tx,rx)
rxDelay = 20
Отобразите информацию об эквалайзере. Значение задержки указывает на задержку, введенную эквалайзером. Вычислите общую задержку как сумму rxDelay и задержки эквалайзера.
eqInfo = info(lineq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency;
Пока эквалайзер, вывод сходится, коэффициент ошибок символа, не высок. Постройте вывод ошибок, err1, чтобы определить, когда компенсируемый вывод будет сходиться.
plot(abs(err1)) xlabel('Symbols') ylabel('Error Magnitude') title('Equalizer Error Signal')

График показывает чрезмерные ошибки вне этих 1 000 периодов подготовки символов. Когда демодуляция символов и вычислительных ошибок символа, чтобы составлять не сходившийся вывод и системную задержку между эквалайзером вывод и переданными символами, пропускает первые 2 000 символов.
dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4); symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 5999
evmWithDelay = evm(y1)
evmWithDelay = 29.5795
Коэффициент ошибок и EVM высоки, потому что получить задержка не составлялась в Системном объекте эквалайзера.
Настройте входную задержку эквалайзера
Компенсируйте полученные данные при помощи значения задержки, чтобы установить свойство InputDelay. Поскольку InputDelay является ненастраиваемым свойством, необходимо выпустить Системный объект lineq, чтобы реконфигурировать свойство InputDelay. Компенсируйте полученные символы.
release(lineq) lineq.InputDelay = rxDelay
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 9
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 5
InputDelay: 20
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
[y2,err2,wts2] = lineq(rx,tx(1:numTrainingSymbols,1));
Постройте веса касания и компенсируемое ошибочное значение. Диаграмма стебель-листья показывает, что веса касания эквалайзера до и после системной задержки удалены. 2D график показывает более медленную сходимость эквалайзера для задержанного сигнала, по сравнению с сигналом с удаленной задержкой.
subplot(2,1,1) stem([real(wts1),real(wts2)]) xlabel('Taps') ylabel('Tap Weight Real') legend('rxDelayed','rxDelayRemoved') grid on subplot(2,1,2) stem([imag(wts1),imag(wts2)]) xlabel('Taps') ylabel('Tap Weight Imaginary') legend('rxDelayed','rxDelayRemoved') grid on

figure plot([abs(err1),abs(err2)]) xlabel('Symbols') ylabel('Error Magnitude') legend('rxDelayed','rxDelayRemoved') grid on

Постройте вывод ошибок компенсируемых сигналов, rxDelayed и rxDelayRemoved. Для сигнала, которому удалили задержку, эквалайзер сходится во время 1 000 периодов подготовки символа. Когда демодуляция символов и вычислительных ошибок символа, чтобы составлять не сходившийся вывод и системную задержку между эквалайзером вывод и переданными символами, пропускает первые 500 символов. Реконфигурирование эквалайзера, чтобы составлять системную задержку включает лучшую коррекцию сигнала и уменьшает ошибки символа и EVM.
eqInfo = info(lineq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency; dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4); symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0
evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 9.4435
Эта модель показывает поведение выбранного адаптивного эквалайзера в линии связи с исчезающим каналом. Передатчик и получатель имеют повышенный косинус корня фильтрация импульсной формы. Блок подсистемы позволяет вам выбирать между линейным или эквалайзерами обратной связи решения с помощью наименьшее количество среднего квадратичного (LMS) или рекурсивного наименьшего квадрата (RLS) адаптивный алгоритм.
Структура модели
Передатчик генерирует 16QAM случайные данные сигнала, который включает обучающую последовательность и применяется, корень повысил косинус фильтрация импульсной формы.
Нарушения канала включают многопутевое исчезновение, эффект Доплера, смещение несущей частоты, переменную целочисленную задержку, потерю пути к свободному пространству и AWGN.
Получатель применяется, корень повысил косинус фильтрация импульсной формы, AGC, включает управление режимом эквалайзера, чтобы включить обучение и позволяет вам выбирать алгоритм эквалайзера из этого выбора:

Модель также использует осциллографы, которые могут помочь вам понять, как различные эквалайзеры и адаптивные алгоритмы ведут себя.
Исследуйте модель в качестве примера

Экспериментирование с моделью
Эта модель обеспечивает несколько способов для вас изменить настройки и наблюдать результаты. InitFcn, найденный в File>Model Properties>Callbacks, вызывает slex_adaptive_eq_with_fading_init, чтобы инициализировать модель. Этот файл позволяет вам отличаться настройки по модели, включая:
Системные параметры, такие как ОСШ.
Импульсные параметры формирующий фильтра, такие как спад и длина фильтра
Значение пути потерь.
Условия канала: Rayleigh или исчезновение Rician, усиления пути к каналу, задержки пути к каналу, эффект Доплера.
Выбор эквалайзера и настройка.
Образцовые факторы
Эта нестандартизированная линия связи является представительной для современной системы связи.
Оптимальная настройка эквалайзера зависит от условий канала. Файл инициализации устанавливает эффект Доплера и многопутевые исчезающие параметры канала, которые подсвечивают возможности различных эквалайзеров.

Структура эквалайзера обратной связи решения выполняет лучше, чем линейная структура эквалайзера для более высокой интерференции межсимвола.
Алгоритм RLS выполняет лучше, чем LMS-алгоритм для более высоких Доплеровских частот.
LMS-алгоритм выполняется быстро, медленно сходится, и его сложность растет линейно с количеством весов.
Алгоритм RLS сходится быстро, его сложность растет примерно как квадрат количества весов и может быть нестабильной, когда количество весов является большим.
Канал, осуществленный для различных эквалайзеров, имеет следующие характеристики:

Начальные установки для других нарушений канала являются тем же самым для всех эквалайзеров. Значение смещения несущей частоты установлено к 50 Гц. Потеря пути к свободному пространству установлена в 60 дБ. Переменная целочисленная задержка установлена в 2 выборки, который требует, чтобы эквалайзеры выполнили некоторое восстановление синхронизации.
Глубокий канал исчезает, и потеря пути может заставить уровень входного сигнала эквалайзера быть намного меньше, чем желаемый уровень выходного сигнала и приводить к неприемлемо длинному времени сходимости эквалайзера. Блок AGC настраивает значение полученного сигнала уменьшать время сходимости эквалайзера. Оптимальный уровень выходной мощности AGC должен быть настроен на основе выбранной схемы модуляции. Для 16QAM, используется желаемая выходная мощность 10 Вт.
Обучение эквалайзера выполняется в начале симуляции.
Выполнение симуляции
Выполнение симуляции вычисляет ошибочную статистику символа и производит эти фигуры:
Схема совокупности сигнала после получить фильтра.
Схема совокупности сигнала после AGC.
Схема совокупности сигнала после коррекции с показанными измерениями качества сигнала.
Диаграмма погрешностей эквалайзера.
Для графиков, показанных здесь, выбранным алгоритмом эквалайзера является RLS Linear. Контролируя эти фигуры, вы видите, что полученное качество сигнала колеблется, в то время как время симуляции прогрессирует.
После Фильтра Rx и После того, как графики совокупности AGC показывают сигнал перед коррекцией. После того, как AGC показывает влияние условий канала на переданном сигнале. После того, как график Eq показывает сигнал после коррекции. Сигнал, построенный в схеме совокупности после коррекции, показывает изменение в качестве сигнала на основе эффективности процесса коррекции. В течение симуляции, сигналы, построенные перед коррекцией, отклоняются заметно от 16QAM сигнальное созвездие. После того, как совокупность Eq улучшается или ухудшается, когда сигнал ошибки эквалайзера отличается. Узкий скачок в начале Диаграммы погрешностей Eq, указывает на плохую коррекцию в начале симуляции. Эквалайзер сходится быстро, но между 5 и 6 мс канал, исчезающий, условия ухудшаются и ошибочные увеличения эквалайзера.




Дальнейшее исследование
Дважды кликните блок Equalizer Selector и выберите различный эквалайзер. Запустите симуляцию, чтобы видеть производительность различных опций эквалайзера. Можно использовать регистратор сигнала, чтобы сравнить результаты этого экспериментирования. Щелкните правой кнопкой по сигнальным проводам в блок-схеме и выберите Log Selected Signals.
В командной строке MATLAB™ введите edit slex_adaptive_eq_with_fading_init.m, чтобы открыть файл инициализации, затем изменить параметр и повторно выполнить симуляцию. Если вы включили журналирование сигнала, после того, как симуляция запустит концы, откроет Инспектора Данных моделирования, чтобы просмотреть регистрируемые сигналы. Например:
Настройте характеристики канала (params.maxDoppler |, params.pathDelays и params.pathGains). Адаптивный алгоритм RLS выполняет лучше, чем адаптивный алгоритм LMS как максимум, Доплер увеличен.