Приближение сплайнами продукта Tensor

Поскольку тулбокс может обработать сплайны с векторными коэффициентами, легко реализовать интерполяцию или приближение к данным с координатной сеткой сплайнами продукта тензора, когда следующий рисунок предназначается, чтобы показать. Можно также запустить пример “Двумерные Сплайны продукта Tensor”.

Безусловно, большая часть приближения сплайна продукта тензора к данным с координатной сеткой может быть получена непосредственно с одной из команд конструкции сплайна, как spapi или csape, в этом тулбоксе, без беспокойства о деталях, обсужденных в этом примере. Скорее этот пример предназначается, чтобы проиллюстрировать теорию позади конструкции продукта тензора, и это поможет в ситуациях, не покрытых командами конструкции в этом тулбоксе.

В этом разделе рассматриваются эти аспекты проблемы сплайна продукта тензора:

Выбор сайтов и узлов

Считайте, например, приближение наименьших квадратов к определенным данным z (i, j) =f (x (i), y (j)), i =1:Nx, j =1:Ny. Вы берете данные из функции, используемой экстенсивно Франке для тестирования схем подбора кривой поверхности (см. Р. Франке, “Критическое сравнение некоторых методов для интерполяции данных, имеющий разброс”, Высшая школа ВМС США Techn. Член палаты представителей NPS 53-79-003, март 1979). Его область является модульным квадратом. Вы выбираете еще несколько сайтов данных в x - направлении, чем y - направление; также, для лучшего определения, вы используете более высокую плотность данных около контура.

x = sort([(0:10)/10,.03 .07, .93 .97]);
y = sort([(0:6)/6,.03 .07, .93 .97]);
[xx,yy] = ndgrid(x,y); z = franke(xx,yy);

Приближение Наименьших квадратов как Функция y

Обработайте эти данные как прибывающий из функции с векторным знаком, а именно, функции y, значением которого в y (j) является векторный z (: j), весь j. Ни по какой конкретной причине примите решение аппроксимировать эту функцию параболическим сплайном с векторным знаком с тремя однородно расположенными с интервалами внутренними узлами. Это означает, что вы выбираете порядок сплайна и последовательность узла для этого сплайна с векторным знаком как

ky = 3; knotsy = augknt([0,.25,.5,.75,1],ky);

и затем используйте spap2, чтобы предоставить аппроксимирующую функцию наименьших квадратов данным:

sp = spap2(knotsy,ky,y,z);

В действительности вы находите одновременно дискретное приближение наименьших квадратов от S _ky,knotsy к каждому из наборов данных Nx

$\begin{matrix} {(y (j), z (i, j))}_{j = 1}^{N y}, & i = 1 : N x \end{matrix}$

В частности, операторы

yy = -.1:.05:1.1;
vals = fnval(sp,yy);

предоставьте массиву vals, запись которого vals(i,j) может быть взят в качестве приближения к значению f (x (i), yy (j)) базового функционального f в точке mesh x (i), yy (j), потому что vals(:,j) является значением в yy (j) сплайновой кривой приближения в sp.

Это очевидно в следующей фигуре, полученной командой:

mesh(x,yy,vals.'), view(150,50)

Отметьте использование vals.', в команде mesh, необходимой из-за MATLAB^®, ориентированного на матрицу на представление при графическом выводе массива. Это может быть серьезной проблемой в двумерном приближении, потому что там это обычно, чтобы думать о z (i, j) как значение функции в точке (x (i), y (j)), в то время как MATLAB думает о z (i, j) как значение функции в точке (x (j), y (i)).

Семейство плавных кривых, симулирующих быть поверхностью

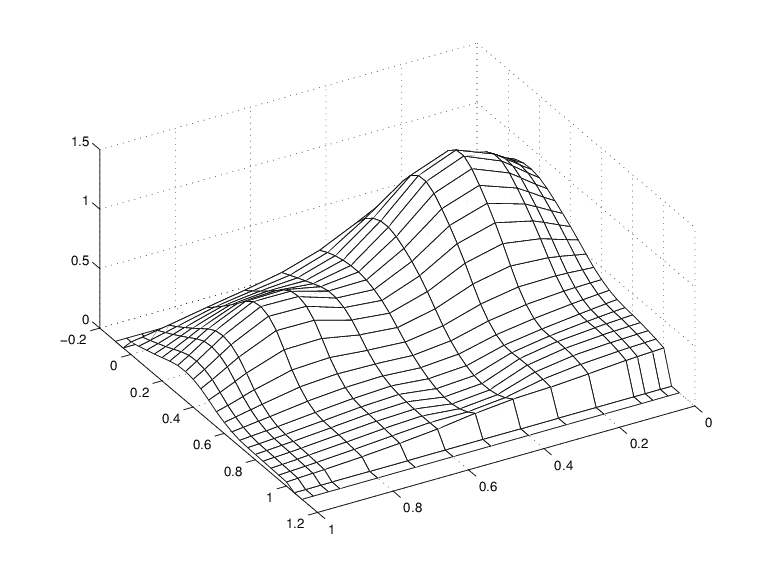
Обратите внимание на то, что и первые два и последние два значения на каждой плавной кривой являются на самом деле нулем, потому что и первые два и последние два сайта в yy вне основного интервала для сплайна в sp.

Отметьте также гребни. Они подтверждают, что вы строите плавные кривые в одном направлении только.

Приближение к Коэффициентам как Функции x

Чтобы получить фактическую поверхность, теперь необходимо пойти шаг вперед. Посмотрите на коэффициенты coefsy сплайна в sp:

coefsy = fnbrk(sp,'coefs');

Абстрактно, можно думать о сплайне в sp как функция

$y | \to \sum_{r} c o e f s y (:, r) B_{r, k y} (y)$

с i th запись coefsy(i,r) векторного коэффициента coefsy(:,r), соответствующий x (i), для всего i. Это предлагает аппроксимировать каждый вектор коэффициентов coefsy(q,:) сплайном того же порядка kx и с той же соответствующей последовательностью узла knotsx. Ни по какой конкретной причине на этот раз используйте кубические сплайны с четырьмя однородно расположенными с интервалами внутренними узлами:

kx = 4; knotsx = augknt([0:.2:1],kx); 
sp2 = spap2(knotsx,kx,x,coefsy.');

Обратите внимание на то, что spap2 (knots,k,x,fx) ожидает, что fx (:,j) будет данной величиной в x(j), т.е. ожидает, что каждый столбец fx будет значением функции. Соответствовать данной величине coefsy(q, :) в x (q), для всего q, существовать spap2 с транспонированием coefsy.

Двумерное приближение

Теперь рассмотрите транспонирование коэффициентов cxy получившейся сплайновой кривой:

coefs = fnbrk(sp2,'coefs').';

Это обеспечивает приближение двумерного сплайна

$(x, y) | \to \sum_{q} \sum_{r} c o e f s (q, r) B_{q, k x} (x) B_{r, k y} (y)$

к исходным данным

$(x (i), y (j)) | \to z (x (i), y (j)), i = 1 : N x, j = 1 : N y$

Чтобы построить этот сплайн появляются по сетке, например, сетке

xv = 0:.025:1; yv = 0:.025:1;

можно сделать следующее:

values = spcol(knotsx,kx,xv)*coefs*spcol(knotsy,ky,yv).'; 
mesh(xv,yv,values.'), view(150,50);

Это приводит к следующей фигуре.

Приближение сплайна к функции Франке

Это проявляет здравый смысл, потому что spcol(knotsx,kx,xv) является матрицей, чья (i, q) th запись равняется значению B_{q, kx} (xv (i)) в xv (i) q th B-сплайн порядка kx для последовательности узла knotsx.

Поскольку матрицы, spcol(knotsx,kx,xv) и spcol(knotsy,ky,yv) соединены, это может быть более эффективно, хотя, возможно, больше потребления памяти, для большого xv и yv, чтобы использовать fnval, можно следующим образом:

value2 = ... 
  fnval(spmak(knotsx,fnval(spmak(knotsy,coefs),yv).'),xv).';

Это, на самом деле, что происходит внутренне, когда fnval называется непосредственно со сплайном продукта тензора, как в

value2 = fnval(spmak({knotsx,knotsy},coefs),{xv,yv});

Вот вычисление относительной погрешности, т.е. различие между определенными данными и значением приближения на тех сайтах данных по сравнению со значением определенных данных:

errors = z - spcol(knotsx,kx,x)*coefs*spcol(knotsy,ky,y).'; 
disp( max(max(abs(errors)))/max(max(abs(z))) )

Выводом является 0.0539, возможно, не слишком впечатляющий. Однако массив коэффициентов только имел размер 8 6

disp(size(coefs))

соответствовать массиву данных размера 15 11.

disp(size(z))

Переключитесь по порядку

Подход, сопровождаемый здесь, кажется смещенным, следующим образом. Сначала думайте об определенных данных z как описание функции с векторным знаком y, и затем обработайте матрицу, сформированную векторными коэффициентами кривой приближения как описание функции с векторным знаком x.

Что происходит, когда вы берете вещи в противоположном порядке, т.е. думаете о z как об описании функции с векторным знаком x, и затем обрабатываете матрицу, составленную от векторных коэффициентов кривой приближения как описание функции с векторным знаком y?

Возможно, удивительно итоговое приближение является тем же самым до округления. Вот числовой эксперимент.

Приближение Наименьших квадратов как Функция x

Во-первых, соответствуйте сплайновой кривой к данным, но на этот раз с x как независимая переменная, следовательно это - строки z, которые теперь становятся значениями данных. Соответственно, необходимо предоставить z.', а не z, к spap2,

spb = spap2(knotsx,kx,x,z.');

таким образом получая приближение сплайна ко всем кривым (x; z: J. В частности, оператор

valsb = fnval(spb,xv).';

обеспечивает матричный valsb, запись которого valsb(i, j) может быть взят в качестве приближения к значению f (xv (i), y (j)) базового функционального f в точке mesh (xv (i), y (j)). Это очевидно, когда вы строите valsb с помощью mesh:

mesh(xv,y,valsb.'), view(150,50)

Другое семейство плавных кривых, симулирующих быть поверхностью

Отметьте гребни. Они подтверждают, что вы, еще раз, строите плавные кривые в одном направлении только. Но на этот раз кривые, запущенные в другом направлении.

Приближение к Коэффициентам как Функции y

Теперь прибывает второй шаг, чтобы получить фактическую поверхность. Во-первых, извлеките коэффициенты:

coefsx = fnbrk(spb,'coefs');

Затем соответствуйте каждому вектору коэффициентов coefsx(r,:) сплайном того же порядка ky и с той же соответствующей последовательностью узла knotsy:

spb2 = spap2(knotsy,ky,y,coefsx.');

Обратите внимание на то, что, еще раз, необходимо транспонировать массив коэффициентов от spb, потому что spap2 берет столбцы своего последнего входного параметра как значения данных.

Соответственно, нет теперь никакой потребности транспонировать массив коэффициентов coefsb получившейся кривой:

coefsb = fnbrk(spb2,'coefs');

Двумерное приближение

Требование состоит в том, что coefsb равняется более раннему массиву коэффициентов coefs, до округления, и здесь является тестом:

disp( max(max(abs(coefs - coefsb))) )

Выводом является 1.4433e-15.

Объяснение достаточно просто: коэффициенты c сплайна s, содержавшийся в sp = spap2(knots,k,x,y), зависят линейно от входных значений y. Это подразумевает, учитывая, что и c и y являются матрицами с 1 строкой, что существует некоторый матричный A =Aknots_{, k, x} так, чтобы

$c = y A_{узлы, k, x}$

для любых данных y. Этот оператор даже содержит, когда y является матрицей размера d-by-N, скажем, в этом случае каждая данная величина y (: j), взят, чтобы быть точкой в R ^d, и получившимся сплайном является соответственно d - с векторным знаком, следовательно его массив коэффициентов, c имеет размер d-by-n с n = length(knots)-k.

В частности, операторы

sp = spap2(knotsy,ky,y,z); 
coefsy =fnbrk(sp,'coefs');

предоставьте нам матричный coefsy, который удовлетворяет

$coefs y = z . A_{knotsy, ky, y}$

Последующие вычисления

 sp2 = spap2(knotsx,kx,x,coefsy.'); 
 coefs = fnbrk(sp2,'coefs').';

сгенерируйте массив коэффициентов coefs, который, учитывая эти два перемещения, удовлетворяет

$\begin{matrix} coefs = ((z A_{knotsy, ky, y})' . A_{knotsx, kx, x})' \\ = (A_{knotsx, kx, x})' . z . A_{knotsy, ky, y} \end{matrix}$

Во втором, альтернативном, вычислении, вы сначала вычислили

 spb = spap2(knotsx,kx,x,z.'); 
 coefsx = fnbrk(spb,'coefs');

следовательно coefsx =z _{'.Aknotsx, kx, x}. Последующее вычисление

 spb2 = spap2(knotsy,ky,y,coefsx.');
 coefsb = fnbrk(spb,'coefs');

затем, если

$coefsb = coefsx .' . A_{knotsy, ky, y} = (A_{knotsx, kx, x}) .' . z . A_{knotsy, ky, y}$

Следовательно, coefsb = coefs.

Сравнение и расширение

Второй подход более симметричен, чем первое в том перемещении происходит в каждом вызове spap2 и больше нигде. Этот подход может использоваться для приближения к данным с координатной сеткой в любом количестве переменных.

Если, например, определенные данные по 3D сетке содержатся в некотором 3D массиве v размера [Nx,Ny,Nz] с v(i,j,k), содержащим значение f (x (i), y (j), z (k)), то вы начались бы с

coefs = reshape(v,Nx,Ny*Nz);

Предположение, что n j = knots j - kj, для j = x,y,z, вы затем продолжили бы можно следующим образом:

sp = spap2(knotsx,kx,x,coefs.');
coefs = reshape(fnbrk(sp,'coefs'),Ny,Nz*nx);
sp = spap2(knotsy,ky,y,coefs.'); 
coefs = reshape(fnbrk(sp,'coefs'),Nz,nx*ny);
sp = spap2(knotsz,kz,z,coefs.'); 
coefs = reshape(fnbrk(sp,'coefs'),nx,ny*nz);

См. Главу 17 PGS или [К. де Бор, “Эффективная манипуляция с компьютерами продуктов тензора”, Математика Сделки ACM. Программное обеспечение 5 (1979), 173–182; Исправления, 525] для получения дополнительной информации. Те же ссылки также ясно дают понять, что нет ничего специального здесь об использовании приближения наименьших квадратов. Любой процесс приближения, включая интерполяцию сплайна, получившееся приближение которой имеет коэффициенты, которые зависят линейно от определенных данных, может быть расширен таким же образом к многомерному процессу приближения к данным с координатной сеткой.

Это точно, что используется в командах конструкции сплайна csapi, csape, spapi, spaps и spap2, когда данные с координатной сеткой должны быть адаптированы. Это также используется в fnval, когда сплайн продукта тензора должен быть оценен на сетке.

Документация