Документация

Рациональный пример сплайна: круг

Например,

circle = rsmak('circle');

обеспечивает рациональный сплайн, значения которого на его основном интервале прослеживают модульный круг, т.е. круг радиуса 1 с центром в начале координат, как команда

fnplt(circle), axis square

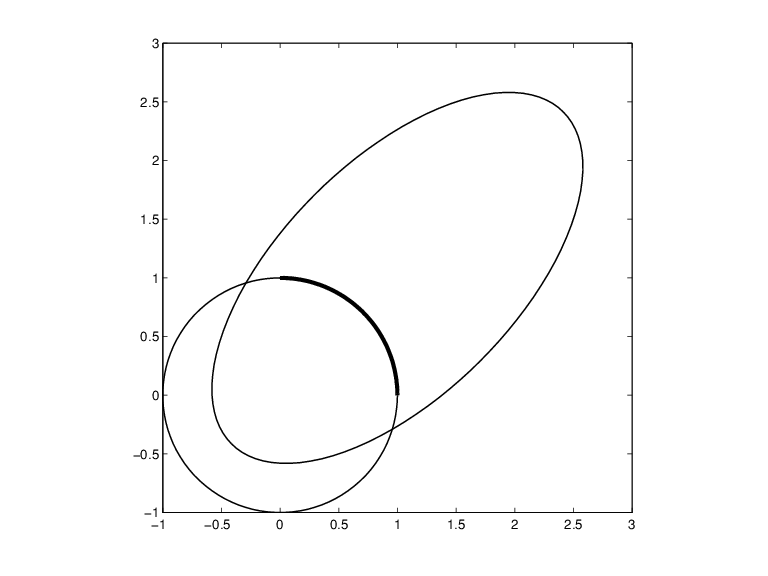
с готовностью показывает; получившийся вывод является кругом в фигуре Круг и Эллипс, Оба Данные Рациональным Сплайном.

Легко управлять этим кругом, чтобы получить связанные формы. Например, следующие команды расширяют круг в эллипс, вращают эллипс 45 градусов, и переводят его (1,1), и затем строят его сверху круга.

ellipse = fncmb(circle,[2 0;0 1]);
s45 = 1/sqrt(2);
rtellipse = fncmb(fncmb(ellipse, [s45 -s45;s45 s45]), [1;1] );
hold on, fnplt(rtellipse), hold off

Как дальнейший пример, "круг", только созданный, соединен от четырех частей. Чтобы подсветить первое такая часть, используйте следующие команды:

quarter = fnbrk(fn2fm(circle,'rp'),1);
hold on, fnplt(quarter,3), hold off

В первой команде fn2fm используется, чтобы изменить формы от одной на основе B-формы одной на основе ppform, и затем fnbrk используется, чтобы извлечь первую часть, и эта часть затем построена сверху круга в Кругу и Эллипсе, Оба Данные Рациональным Сплайном, с linewidth 3, чтобы заставить его выделиться.

Рациональный пример сплайна: Сфера

Как поверхностный пример, команда rsmak('southcap') обеспечивает ценный рациональный bicubic полином с 3 векторами чьи значения на модульном квадрате [-1.. 1] ^2 заполняют часть сферы единичного радиуса. Примкните к нему, пять подходящих вращаются его, и вы получаете сферу единичного радиуса точно. Для рисунка следующие команды генерируют две трети той сферы, как показано в части Сферы, Сформированной Четыре, Вращается Биквадратного Рационального.

southcap = rsmak('southcap'); fnplt(southcap)
xpcap = fncmb(southcap,[0 0 -1;0 1 0;1 0 0]);
ypcap = fncmb(xpcap,[0 -1 0; 1 0 0; 0 0 1]);
northcap = fncmb(southcap,-1);
hold on, fnplt(xpcap), fnplt(ypcap), fnplt(northcap)
axis equal, shading interp, view(-115,10), axis off, hold off

Функции для Работы с рациональными сплайнами

Приняв решение представлять рациональный сплайн r = s/w таким образом обычным сплайном R = [s; w] делает, легко примениться к рациональному сплайну все команды fn... в функциях сплайна Curve Fitting Toolbox™ за следующими исключениями. Интеграл рационального сплайна не должен быть рациональным сплайном, следовательно нет никакого способа расширить fnint к рациональным сплайнам. Производная рационального сплайна является снова рациональным сплайном, но одним из примерно дважды порядка. По этой причине fnder и fndir не коснутся рациональных сплайнов. Вместо этого существует команда fntlr для вычисления значения в данном x всех производных до данного распоряжения заданной функции. Если эта функция рациональна, необходимое вычисление основано на внимании, уделенном в предыдущем абзаце.

r = rsmak(shape) команды обеспечивает рациональные сплайны в rBform, которые описывают точно геометрические фигуры определенного стандарта, как 'circle', 'arc', 'cylinder', 'sphere', 'cone', 'torus'. Команда fncmb(r,trans) может использоваться, чтобы применить стандартные преобразования к получившейся форме. Например, если бы trans является вектор-столбцом правильной длины, форма была бы переведена тем вектором, в то время как, если бы trans является подходящей матрицей как вращение, форма была бы преобразована той матрицей.

Команда r = rscvn(p) создает квадратичный rBform непрерывной кривой касательной, составленной из круговых дуг и прохождения через данную последовательность, p, точек в плоскости.

Специальная рациональная форма сплайна, названная NURBS, стала стандартным инструментом в CAGD. NURBS является, по определению, любым рациональным сплайном, для которого и s и w находятся в той же B-форме с каждым коэффициентом для s, содержащего явным образом соответствующий коэффициент для w как фактор:

Нормированные коэффициенты a (: i), поскольку сплайн числителя с большей готовностью используются в качестве контрольных точек, чем ненормированные коэффициенты v (i) a (: i) используемый в rBform. Тем не менее, этот тулбокс не обеспечивает специальной формы NURBS, но только более общего рационального сплайна, но в обеих B-формах (названный rBform внутренне) и в ppform (названный rpform внутренне).

Рациональный сплайн, который circle использовал ранее, соединен в rsmak кодом как следующее.

x = [1 1 0 -1 -1 -1  0  1 1]; y = [0 1 1  1  0 -1 -1 -1 0];
s45 = 1/sqrt(2); w =[1 s45 1 s45 1 s45 1 s45 1];
circle = rsmak(augknt(0:4,3,2), [w.*x;w.*y;w]);

Отметьте внешний вид сплайна знаменателя как последний компонент. Также отметьте, как коэффициенты сплайна знаменателя появляются здесь явным образом как факторы соответствующих коэффициентов сплайна числителя. Нормированная содействующая последовательность [x;y] очень проста; это состоит из вершин и средних точек, в соответствующем порядке, "модульного квадрата". Получившийся полигон управления является касательной к кругу в местах, где четыре квадратичных части, которые формируют круг, примыкают.

Для полного обсуждения NURBS смотрите [Г. Фэрина, NURBS, 2-го редактора, AKPeters Ltd, 1999] или [Les Piegl и Уэйн Тиллер, Книга NURBS, 2-й редактор, Springer-Verlag, 1997].