Интерполяция является процессом для оценки значений, которые находятся между известными точками данных.
Методы Interpolant
Метод | Описание |
|---|---|
Линейный | Линейная интерполяция. Этот метод соответствует различному линейному полиному между каждой парой точек данных для кривых, или между наборами трех точек для поверхностей. |
NearestNeighbor | Самая близкая соседняя интерполяция. Этот метод устанавливает значение интерполированной точки к значению самой близкой точки данных. Поэтому этот метод не генерирует новых точек данных. |
Кубический сплайн | Интерполяция кубическим сплайном. Этот метод соответствует различному кубическому полиному между каждой парой точек данных для кривых, или между наборами трех точек для поверхностей. |
Сохранение формы | Кусочная кубическая интерполяция Эрмита (PCHIP). Этот метод сохраняет монотонность и форму данных. Для кривых только. |
Бигармонический (v4) | Метод MATLAB® 4 Для поверхностей только. |
Сплайн тонкой пластины | Интерполяция сплайна тонкой пластины. Этот метод соответствует сглаженным поверхностям, которые также экстраполируют хорошо. Для поверхностей только. |
Для поверхностей тип подгонки Interpolant использует функцию scatteredInterpolant MATLAB для линейных и самых близких методов и функцию griddata MATLAB для кубических и бигармонических методов. Метод сплайна тонкой пластины использует функцию tpaps.
Тип interpolant, чтобы использовать зависит от характеристик данных, являющихся подходящим, необходимая гладкость кривой, факторов скорости, постподходящих аналитических требований, и так далее. Линейные и самые близкие соседние методы быстры, но получившиеся кривые не очень сглаженны. Кубический сплайн и сохранение формы и v4 методы медленнее, но получившиеся кривые очень сглаженны.
Например, ядерные данные о реакции из файла carbon12alpha.mat показывают здесь с самой близкой соседней подгонкой interpolant и сохранением формы (PCHIP) interpolant подгонка. Безусловно, самый близкий соседний interpolant не следует за данными, а также сохранением формы interpolant. Различие между этими двумя подгонками может быть важным, если вы интерполируете. Однако, если вы хотите интегрировать данные, чтобы получить смысл общей силы реакции, затем обе подгонки предоставляют почти идентичные ответы для разумных ширин интервала интегрирования.
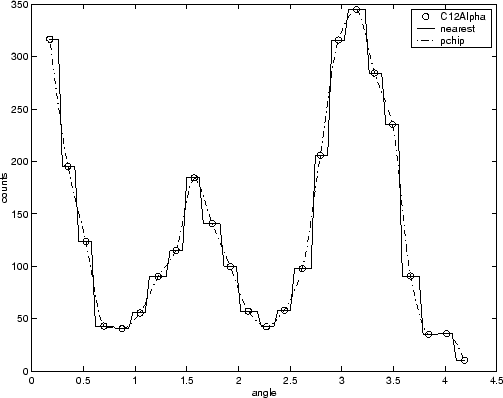
Статистика качества подгонки, границы прогноза и веса не заданы для interpolants. Кроме того, подходящие невязки всегда 0 (в компьютерной точности), потому что interpolants проход через данные указывает.
Interpolants заданы как кусочные полиномы, потому что кривая по экспериментальным точкам создается из многих “частей” (за исключением Biharmonic для поверхностей, который является радиальной основной функцией interpolant). Для кубического сплайна и интерполяции PCHIP, каждая часть описана четырьмя коэффициентами, которые тулбокс вычисляет использование кубического полинома (третьей степени).
Обратитесь к функции spline для получения дополнительной информации об интерполяции кубическим сплайном.
Обратитесь к функции pchip для получения дополнительной информации о сохраняющей форму интерполяции, и для сравнения этих двух методов.
Обратитесь к scatteredInterpolant, griddata и функциям tpaps для получения дополнительной информации о поверхностной интерполяции.
Возможно соответствовать одному “глобальному” полиному interpolant к данным со степенью меньше, чем количество точек данных. Однако такая подгонка может иметь дико ошибочное поведение между точками данных. Напротив, кусочные многочлены, определенные здесь всегда, производят подгонку хорошего поведения, таким образом, они более гибки, чем параметрические полиномы и могут эффективно использоваться для более широкой области значений наборов данных.