дифференцироваться

Объект Differentiate cfit или sfit

Синтаксис

fx = differentiate(FO, X) [fx, fxx] = differentiate(...) [fx, fy] = differentiate(FO, X, Y) [fx, fy] = differentiate(FO, [x, y]) [fx, fy, fxx, fxy, fyy] = differentiate(FO, ...)

Описание

Для кривых

fx = differentiate(FO, X) дифференцирует объект cfit FO в точках, заданных векторным X, и возвращает результат в fx.

[fx, fxx] = differentiate(...) также возвращает вторую производную в fxx.

Все возвращаемые аргументы одного размера и формируют как X.

Для поверхностей

[fx, fy] = differentiate(FO, X, Y) дифференцирует поверхностный FO в точках, заданных X и Y, и возвращает результат в fx и fy.

FO является поверхностным подходящим объектом (sfit), сгенерированным функцией fit.

X и Y должны быть массивами с двойной точностью и тем же размером и формой друг как друг.

Все возвращаемые аргументы одного размера и формируют как X и Y.

Если FO представляет поверхность $z = f (x, y)$ , затем FX содержит производные относительно x, то есть, $\frac{d f}{d x}$ , и FY содержит производные относительно y, то есть, $\frac{d f}{d y}$ .

[fx, fy] = differentiate(FO, [x, y]), то, где X и Y являются вектор-столбцами, позволяет вам задавать точки оценки как отдельный аргумент.

[fx, fy, fxx, fxy, fyy] = differentiate(FO, ...) вычисляет первые и вторые производные поверхностного подходящего объекта FO.

fxx содержит вторые производные относительно x, то есть, $\frac{\partial^{2} f}{\partial x^{2}}$ .

fxy содержит смешанные вторые производные, то есть, $\frac{\partial^{2} f}{\partial x \partial y}$ .

fyy содержит вторые производные относительно y, то есть, $\frac{\partial^{2} f}{\partial y^{2}}$ .

Примеры

Для кривых

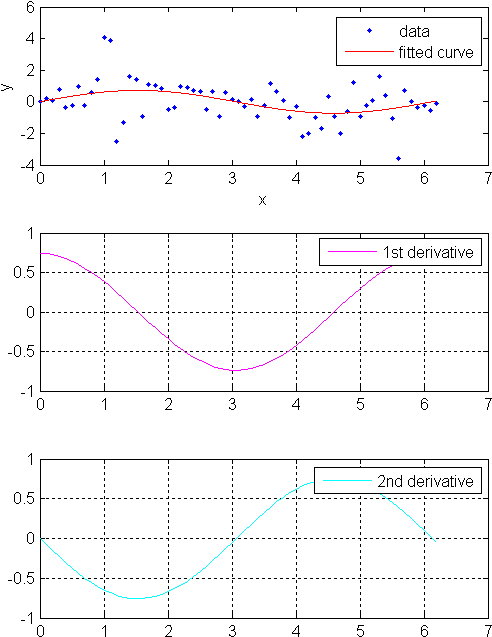
Создайте базовый синусоидальный сигнал:

xdata = (0:.1:2*pi)';
y0 = sin(xdata);

Добавьте зависимый ответом Гауссов шум в сигнал:

noise = 2*y0.*randn(size(y0)); 											
ydata = y0 + noise;

Соответствуйте шумным данным пользовательской синусоидальной моделью:

f = fittype('a*sin(b*x)');
fit1 = fit(xdata,ydata,f,'StartPoint',[1 1]);

Найдите производные сглаженной функции в предикторах:

[d1,d2] = differentiate(fit1,xdata);

Отобразите на графике данные, подгонку и производные:

subplot(3,1,1)
plot(fit1,xdata,ydata) % cfit plot method
subplot(3,1,2)
plot(xdata,d1,'m') % double plot method
grid on
legend('1st derivative')
subplot(3,1,3)
plot(xdata,d2,'c') % double plot method
grid on
legend('2nd derivative')

Можно также вычислить и построить производные непосредственно с методом plot cfit, можно следующим образом:

plot(fit1,xdata,ydata,{'fit','deriv1','deriv2'})

Метод plot, однако, не возвращает данные по производным, в отличие от метода differentiate.

Для поверхностей

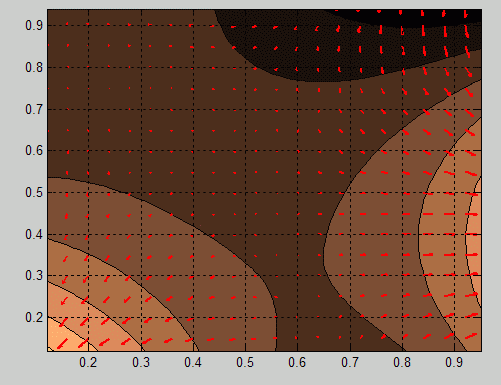
Можно использовать метод differentiate, чтобы вычислить градиенты подгонки и затем использовать функцию quiver, чтобы построить эти градиенты как стрелки. Следующий пример строит градиенты поверх контурного графика.

x = [0.64;0.95;0.21;0.71;0.24;0.12;0.61;0.45;0.46;...
0.66;0.77;0.35;0.66];
y = [0.42;0.84;0.83;0.26;0.61;0.58;0.54;0.87;0.26;...
0.32;0.12;0.94;0.65];
z = [0.49;0.051;0.27;0.59;0.35;0.41;0.3;0.084;0.6;...
0.58;0.37;0.19;0.19];
fo = fit( [x, y], z, 'poly32', 'normalize', 'on' );
[xx, yy] = meshgrid( 0:0.04:1, 0:0.05:1 );

[fx, fy] = differentiate( fo, xx, yy );

plot( fo, 'Style', 'Contour' );
hold on
h = quiver( xx, yy, fx, fy, 'r', 'LineWidth', 2 );
hold off
colormap( copper )

Если вы хотите использовать производные в оптимизации, можно, например, реализовать целевую функцию для fmincon можно следующим образом.

function [z, g, H] = objectiveWithHessian( xy )
        % The input xy represents a single evaluation point
        z = f( xy );
        if nargout > 1
            [fx, fy, fxx, fxy, fyy] = differentiate( f, xy );
            g = [fx, fy];
            H = [fxx, fxy; fxy, fyy];
        end
    end

Советы

Для моделей библиотеки с закрытыми формами тулбокс вычисляет производные аналитически. Для всех других моделей тулбокс вычисляет первую производную с помощью отношения приращений в центре

$\frac{d f}{d x} = \frac{f (x + Δ x) - f (x - Δ x)}{2 Δ x}$

где x является значением, в котором тулбокс вычисляет производную, $Δ x$ небольшое число (на порядке кубического корня eps), $f (x + Δ x)$ fun, оцененный в $x + Δ x$ , и $f (x - x Δ)$ fun, оцененный в $x - Δ x$ .

Тулбокс вычисляет вторую производную с помощью выражения

$\frac{d^{2} f}{d x^{2}} = \frac{f (x + Δ x) + f (x - Δ x) - 2 f (x)}{{(Δ x)}^{2}}$

Тулбокс вычисляет смешанную производную для поверхностей с помощью выражения

$\frac{\partial^{2} f}{\partial x \partial y} (x, y) = \frac{f (x + Δ x, y + Δ y) - f (x - Δ x, y + Δ y) - f (x + Δ x, y - Δ y) + f (x - Δ x, y - Δ y)}{4 Δ x Δ y}$

Смотрите также

fit | integrate | plot

Документация

дифференцироваться

Синтаксис

Описание

Примеры

Советы

Смотрите также

Представлено до R2006a

Документация Curve Fitting Toolbox

Поддержка