Распределение Weibull широко используется в надежности и жизни (интенсивность отказов) анализ данных. Тулбокс предоставляет 2D параметру распределение Weibull
где a является масштабным коэффициентом, и b является параметром формы.
Обратите внимание на то, что существуют другие дистрибутивы Weibull, но необходимо создать пользовательское уравнение, чтобы использовать эти дистрибутивы:
Распределение Weibull с тремя параметрами с x, замененным x – c, где c является параметром положения
Адаптировано распределение Weibull с одним параметром, где параметр формы фиксируется и только масштабный коэффициент.
Curve Fitting Toolbox™ не соответствует распределениям вероятностей Weibull к выборке данных. Вместо этого это соответствует кривым к ответу и данным о предикторе, таким образом, что кривая имеет ту же форму как распределение Weibull.
Откройте приложение Curve Fitting путем ввода cftool. Также нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите данные о кривой (X data и Y data, или только Y data против индекса).
Приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели от Polynomial до Weibull.
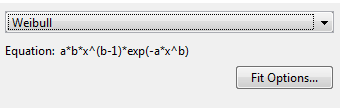
Нет никаких подходящих настроек, чтобы сконфигурировать.
(Необязательно) Нажмите Fit Options, чтобы задать содействующие начальные значения и ограничительные границы, или изменить настройки алгоритма.
Тулбокс вычисляет случайные стартовые точки для моделей Weibull, заданных на интервале [0,1]. Можно заменить стартовые точки и задать собственные значения в Подходящем Окне параметров.
Для получения дополнительной информации о настройках см. Опции Подгонки Определения и Оптимизированные Отправные точки.
Задайте тип модели weibull.
Например, чтобы загрузить некоторые данные в качестве примера, измеряющие концентрацию крови составного объекта против времени, и соответствовать и построить модель Weibull, задающую стартовую точку:
time = [ 0.1; 0.1; 0.3; 0.3; 1.3; 1.7; 2.1;...
2.6; 3.9; 3.9; ...
5.1; 5.6; 6.2; 6.4; 7.7; 8.1; 8.2;...
8.9; 9.0; 9.5; ...
9.6; 10.2; 10.3; 10.8; 11.2; 11.2; 11.2;...
11.7; 12.1; 12.3; ...
12.3; 13.1; 13.2; 13.4; 13.7; 14.0; 14.3;...
15.4; 16.1; 16.1; ...
16.4; 16.4; 16.7; 16.7; 17.5; 17.6; 18.1;...
18.5; 19.3; 19.7;];
conc = [0.01; 0.08; 0.13; 0.16; 0.55; 0.90; 1.11;...
1.62; 1.79; 1.59; ...
1.83; 1.68; 2.09; 2.17; 2.66; 2.08; 2.26;...
1.65; 1.70; 2.39; ...
2.08; 2.02; 1.65; 1.96; 1.91; 1.30; 1.62;...
1.57; 1.32; 1.56; ...
1.36; 1.05; 1.29; 1.32; 1.20; 1.10; 0.88;...
0.63; 0.69; 0.69; ...
0.49; 0.53; 0.42; 0.48; 0.41; 0.27; 0.36;...
0.33; 0.17; 0.20;];
f=fit(time, conc/25, 'Weibull', ...
'StartPoint', [0.01, 2] )
plot(f,time,conc/25, 'o');Если вы хотите изменить подходящие опции, такие как содействующие начальные значения, и ограничительные границы, подходящие для ваших данных, или изменить настройки алгоритма, видят таблицу дополнительных свойств с NonlinearLeastSquares на странице с описанием fitoptions.
Соответствующие значения стартовой точки и масштабирующийся conc/25 для модели Weibull 2D параметра были вычислены путем подбора кривой 3 моделям Weibull параметра с помощью этого пользовательского уравнения:
f=fit(time, conc, ' c*a*b*x^(b-1)*exp(-a*x^b)', 'StartPoint', [0.01, 2, 5] )
f =
General model:
f(x) = c*a*b*x^(b-1)*exp(-a*x^b)
Coefficients (with 95% confidence bounds):
a = 0.009854 (0.007465, 0.01224)
b = 2.003 (1.895, 2.11)
c = 25.65 (24.42, 26.89)
fit | fitoptions | fittype