dsp. NotchPeakFilter

Настраиваемая отметка второго порядка и худой БИХ-фильтр

расширьте все на странице

Описание

Объект NotchPeakFilter фильтрует каждый канал входа с помощью БИХ-реализации фильтра.

Отфильтровать каждый канал входа:

Создайте объект dsp.NotchPeakFilter и установите его свойства.
Вызовите объект с аргументами, как будто это была функция.

Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты? MATLAB.

Создание

Синтаксис

npFilter = dsp.NotchPeakFilter

npFilter = dsp.NotchPeakFilter('Specification','Quality
factor and center frequency')

npFilter = dsp.NotchPeakFilter('Specification','Coefficients')

npFilter = dsp.NotchPeakFilter(Name,Value)

Описание

npFilter = dsp.NotchPeakFilter возвращает отметку второго порядка и худой БИХ-фильтр, который независимо фильтрует каждый канал входа в зависимости от времени, с помощью заданной центральной частоты и пропускной способности на 3 дБ.

npFilter = dsp.NotchPeakFilter('Specification','Quality factor and center frequency') задает добротность (Q фактор) метки или пикового фильтра вместо пропускной способности дБ 3.

npFilter = dsp.NotchPeakFilter('Specification','Coefficients') задает содействующие значения, которые влияют на пропускную способность и центральную частоту непосредственно, вместо того, чтобы задать параметры проекта в Гц. Это удаляет вычисления тригонометрии, включенные, когда свойства настраиваются.

пример

npFilter = dsp.NotchPeakFilter(Name,Value) возвращает фильтр метки с каждым заданным набором имени свойства к заданному значению. Незаданные свойства имеют значения по умолчанию.

Свойства

развернуть все

Если в противном случае не обозначено, свойства являются ненастраиваемыми, что означает, что вы не можете изменить их значения после вызова объекта. Объекты блокируют, когда вы вызываете их, и функция release разблокировала их.

Если свойство является настраиваемым, можно изменить его значение в любое время.

Для получения дополнительной информации об изменении значений свойств смотрите Разработку системы в MATLAB Используя Системные объекты (MATLAB).

`Specification` — Отфильтруйте спецификацию
`'Bandwidth and center frequency'` (значение по умолчанию) | `'Quality factor and center frequency'` | `'Coefficients'`

Установите спецификацию как 'Bandwidth and center frequency', 'Quality factor and center frequency' или 'Coefficients'.

`Пропускная способность` Пропускная способность на 3 дБ
`2205` (значение по умолчанию) | положительная скалярная величина

Задайте пропускную способность дБ 3 фильтра в виде конечного положительного числа в Гц. Значение должно быть скаляром между 0 и половина частоты дискретизации.

Настраиваемый: да

Зависимости

Это свойство применимо, только если Specification является 'Bandwidth and center frequency'.

Типы данных: single | double

`CenterFrequency` — Отметьте или достигните максимума центральная частота
`11025` (значение по умолчанию) | положительная скалярная величина

Задайте центральную частоту фильтра (и для метки и для пика) в виде конечного положительного числа в Гц. Значение должно быть скаляром между 0 и половина частоты дискретизации.

Настраиваемый: да

Зависимости

Это свойство применимо, только если Specification установлен в 'Bandwidth and center frequency' или 'Quality factor and center frequency'.

Типы данных: single | double

`QualityFactor` — Добротность для метки или пикового фильтра
`5` (значение по умолчанию) | положительная скалярная величина

Задайте добротность (Q фактор) и для метки и для пиковых фильтров. Фактор Q задан как центральная частота, разделенная на пропускную способность. Более высокий фактор Q соответствует более узкой метке или пику. Фактором Q должно быть скалярное значение, больше, чем 0.

Настраиваемый: да

Зависимости

Это свойство применимо, только если Specification установлен в 'Quality factor and center frequency'.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi

`SampleRate` — Частота дискретизации входа
`44100` (значение по умолчанию) | положительная скалярная величина

Задайте частоту дискретизации входа в Гц в виде конечного числа.

Типы данных: single | double

`BandwidthCoefficient` — Коэффициент пропускной способности
`0.72654` (значение по умолчанию) | действительный скаляр в области значений [-1 1]

Задайте значение, которое определяет пропускную способность дБ 3 фильтра в виде конечного числа в области значений [-1 1]. Значение -1 соответствует максимальной пропускной способности дБ 3 (SampleRate/4), и 1, соответствует минимальной пропускной способности дБ 3 (0 Гц, фильтру allpass).

Настраиваемый: да

Зависимости

Это свойство только применимо, если Specification установлен в 'Coefficients'.

Типы данных: single | double

`CenterFrequencyCoefficient` — Центральный коэффициент частоты
`0` (значение по умолчанию) | действительный скаляр в области значений [-1 1]

Задайте коэффициент, который определяет центральную частоту фильтра в виде конечного числа в области значений [-1 1]. Значение -1 соответствует минимальной центральной частоте (0 Гц), и 1, соответствует максимальной центральной частоте (Гц SampleRate/2). Значение по умолчанию 0, который соответствует Гц SampleRate/4.

Настраиваемый: да

Зависимости

Это свойство только применимо, если Specification установлен в 'Coefficients'.

Типы данных: single | double

Использование

Для версий ранее, чем R2016b, используйте функцию step, чтобы запустить Систему object™ алгоритм. Аргументы к step являются объектом, который вы создали, сопровождаемый аргументами, показанными в этом разделе.

Например, y = step(obj,x) и y = obj(x) выполняют эквивалентные операции.

Синтаксис

Y = npFilter(x)

[Yn,Yp] = npFilter(x)

Описание

Y = npFilter(x) фильтры каждый канал (столбец) входного сигнала, x, чтобы произвести фильтр метки вывод, Y.

[Yn,Yp] = npFilter(x) фильтры каждый канал входного сигнала, x, чтобы произвести фильтр метки вывод, Yn и пиковый фильтр вывод, Yp.

Входные параметры

развернуть все

`x` Входной сигнал
вектор | матрица

Входной сигнал, заданный как вектор или матрица.

Типы данных: single | double
Поддержка комплексного числа: Да

Выходные аргументы

развернуть все

`Yn` — Отметьте фильтруют вывод
вектор | матрица

Отметьте фильтруют выходной параметр, возвращенный как вектор или матрица.

Типы данных: single | double
Поддержка комплексного числа: Да

`Yp` Достигните максимума выведенный фильтр
вектор | матрица

Пиковый фильтр выходной параметр, возвращенный как вектор или матрица.

Типы данных: single | double
Поддержка комплексного числа: Да

Функции объекта

Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:

release(obj)

развернуть все

Характерный для dsp.NotchPeakFilter

`getBandwidth`	Получите пропускную способность на 3 дБ
`getCenterFrequency`	Получите центральную частоту
`getOctaveBandwidth`	Пропускная способность в количестве октав
`getQualityFactor`	Получите добротность
`tf`	Передаточная функция

Характерный для всех системных объектов

`step`	Запустите алгоритм Системного объекта
`release`	Высвободите средства и позвольте изменения в значениях свойств Системного объекта и введите характеристики
`reset`	Сбросьте внутренние состояния Системного объекта

Примеры

развернуть все

Отметьте фильтр

Открыть скрипт

Этот пример показывает, как использовать dsp. NotchPeakFilter как фильтр метки с центральной частотой 5 000 Гц и пропускной способностью на 3 дБ 500 Гц.

Примечание: Этот пример запускается только в R2016b или позже. Если вы используете более ранний релиз, заменяете каждый вызов функции с эквивалентным синтаксисом step. Например, myObject (x) становится шагом (myObject, x).

npFilter = dsp.NotchPeakFilter('CenterFrequency',5000,'Bandwidth',500);
sa =  dsp.SpectrumAnalyzer('SampleRate',44100,...
    'PlotAsTwoSidedSpectrum',false,'SpectralAverages',50);
for i=1:5000
    y = npFilter(randn(1024,1));
    sa(y);
    if (i==2500)
        % Tune center frequency to 10000
        npFilter.CenterFrequency = 10000;
    end
end
release(npFilter)
release(sa)

Получите Пропускную способность на 3 дБ Фильтра Пика Метки

Скрипт Open Live Script

Создайте объект dsp.NotchPeakFilter с набором свойств Specification к 'Quality factor and center frequency'. Добротность по умолчанию Q равняется 5 и центральной частоте, ФК составляет 11 025 Гц.

np = dsp.NotchPeakFilter('Specification','Quality factor and center frequency')

np = 
  dsp.NotchPeakFilter with properties:

      Specification: 'Quality factor and center frequency'
      QualityFactor: 5
    CenterFrequency: 11025
         SampleRate: 44100

Вычислите пропускную способность на 3 дБ фильтра пика метки с помощью функции getBandwidth. Пропускная способность вычисляется как отношение центральной частоты и добротности, $\frac{ФК}{Q}$ .

getBandwidth(np)

ans = 2205

Визуализируйте ответ фильтра с помощью fvtool.

fvtool(np)

Получите центральную частоту фильтра пика метки

Скрипт Open Live Script

Создайте объект dsp.NotchPeakFilter с набором свойств Specification к 'Coefficients'.

np = dsp.NotchPeakFilter('Specification','Coefficients')

np = 
  dsp.NotchPeakFilter with properties:

                 Specification: 'Coefficients'
          BandwidthCoefficient: 0.7265
    CenterFrequencyCoefficient: 0
                    SampleRate: 44100

Определите центральную частоту фильтра пика метки с помощью функции getCenterFrequency. Когда Specification установлен в 'Coefficients', центральная частота определяется от значения CenterFrequencyCoefficient и частоты дискретизации.

getCenterFrequency(np)

ans = 11025

Визуализируйте ответ фильтра с помощью fvtool.

fvtool(np)

Получите пропускную способность октавы фильтра пика метки

Скрипт Open Live Script

Создайте объект dsp.NotchPeakFilter в настройке по умолчанию.

np = dsp.NotchPeakFilter

np = 
  dsp.NotchPeakFilter with properties:

      Specification: 'Bandwidth and center frequency'
          Bandwidth: 2205
    CenterFrequency: 11025
         SampleRate: 44100

Определите пропускную способность октавы фильтра с помощью функции getOctaveBandwidth.

getOctaveBandwidth(np)

ans = 0.2881

Визуализируйте ответ фильтра с помощью fvtool.

fvtool(np)

Вычислите добротность фильтра пика метки

Скрипт Open Live Script

Создайте объект dsp.NotchPeakFilter в настройке по умолчанию, где свойство Specification установлено в 'Bandwidth and center frequency'.

np = dsp.NotchPeakFilter

np = 
  dsp.NotchPeakFilter with properties:

      Specification: 'Bandwidth and center frequency'
          Bandwidth: 2205
    CenterFrequency: 11025
         SampleRate: 44100

Определите добротность фильтра с помощью функции getQualityFactor. Добротность дана отношением центральной частоты к пропускной способности.

getQualityFactor(np)

ans = 5

Визуализируйте ответ фильтра с помощью fvtool.

fvtool(np)

Определите передаточную функцию фильтра пика метки

Скрипт Open Live Script

Создайте Систему dsp.NotchPeakFilter object™. Получите коэффициенты передаточной функции, соответствующей метке и пиковым фильтрам.

notchpeak = dsp.NotchPeakFilter;
[Bnotch,Anotch,Bpeak,Apeak] = tf(notchpeak)

Bnotch = 1×3

    0.8633   -0.0000    0.8633

Anotch = 1×3

    1.0000   -0.0000    0.7265

Bpeak = 1×3

    0.1367         0   -0.1367

Apeak = 1×3

    1.0000   -0.0000    0.7265

Bnotch и Anotch являются векторами числителя и коэффициентов знаменателя для эквивалентной передаточной функции, соответствующей фильтру метки. Bpeak и Apeak являются векторами числителя и коэффициентов знаменателя для эквивалентной передаточной функции, соответствующей пиковому фильтру.

Алгоритмы

Уравнение проекта для пикового фильтра:

$H (z) = (1 - b) \frac{1 - z^{- 2}}{1 - 2 b потому что w_{0} z^{- 1} + (2 b - 1) z^{- 2}}$

Уравнение проекта для фильтра метки:

$H (z) = b \frac{1 - 2 потому что w_{0} z^{- 1} + z^{- 2}}{1 - 2 b потому что w_{0} z^{- 1} + (2 b - 1) z^{- 2}}$

$b = \frac{1}{1 + загар (Δ w / 2)}$

то, где ω0 = 2πf0/fs является центральной частотой в радианах/выборке (f0 является центральной частотой в Гц, и фс является частотой дискретизации в Гц). Δω = 2πΔf/fs является пропускной способностью на 3 дБ в радианах/выборке (Δf, пропускная способность на 3 дБ в Гц). Обратите внимание на то, что два фильтра дополнительны:

$\begin{array}{l} H_{метка} (z) + H_{пик} (z) = \\ 1they может быть записан как: \\ H_{пик} (z) = \frac{}{12} [1 - A (z)] \\ H_{метка} (z) = \frac{}{12} [1 + A (z)] \\ где A (z) 2^{без обозначения даты} закажите фильтр allpass . \\ A (z) = \frac{a_{2} + a_{1} z^{- 1} + z^{- 2}}{1 + a_{1} z^{- 1} + a_{2} z^{- 2}} \\ и \\ a_{1} = - 2 b потому что ω_{0} \\ a_{2} = 2 b - 1 \end{array}$

Фильтр реализован можно следующим образом:

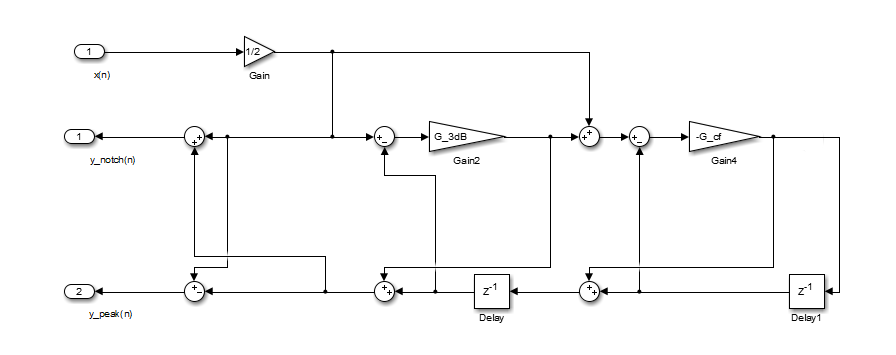
где

$\begin{array}{l} G_{3 дБ} = a_{2} = 2 b - 1 \\ G_{cf} = \frac{a_{1} - a_{1} a_{2}}{1 - a_{2}^{2}} = - потому что w_{0} \end{array}$

Заметьте, что G _cf зависит только от центральной частоты и G_{, 3 дБ} зависят только от пропускной способности на 3 дБ.

Ссылки

[1] Orfanidis, Софокл Дж. Введение в обработку сигналов. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1996.

Смотрите также

Функции

getBandwidth | getCenterFrequency | getOctaveBandwidth | getQualityFactor | iirnotch | iirpeak | tf

Документация

dsp. NotchPeakFilter

Описание

Создание

Синтаксис

Описание

Свойства

Specification — Отфильтруйте спецификацию 'Bandwidth and center frequency' (значение по умолчанию) | 'Quality factor and center frequency' | 'Coefficients'

Пропускная способность Пропускная способность на 3 дБ 2205 (значение по умолчанию) | положительная скалярная величина

Зависимости

CenterFrequency — Отметьте или достигните максимума центральная частота 11025 (значение по умолчанию) | положительная скалярная величина

Зависимости

QualityFactor — Добротность для метки или пикового фильтра 5 (значение по умолчанию) | положительная скалярная величина

Зависимости

SampleRate — Частота дискретизации входа 44100 (значение по умолчанию) | положительная скалярная величина

BandwidthCoefficient — Коэффициент пропускной способности 0.72654 (значение по умолчанию) | действительный скаляр в области значений [-1 1]

Зависимости

CenterFrequencyCoefficient — Центральный коэффициент частоты 0 (значение по умолчанию) | действительный скаляр в области значений [-1 1]

Зависимости

Использование

Синтаксис

Описание

Входные параметры

x Входной сигнал вектор | матрица

Выходные аргументы

Yn — Отметьте фильтруют вывод вектор | матрица

Yp Достигните максимума выведенный фильтр вектор | матрица

Функции объекта

Примеры

Отметьте фильтр

Получите Пропускную способность на 3 дБ Фильтра Пика Метки

Получите центральную частоту фильтра пика метки

Получите пропускную способность октавы фильтра пика метки

Вычислите добротность фильтра пика метки

Определите передаточную функцию фильтра пика метки

Алгоритмы

Ссылки

Смотрите также

Функции

Системные объекты

Блоки

Введенный в R2014a

Документация DSP System Toolbox

Поддержка

`Specification` — Отфильтруйте спецификацию
`'Bandwidth and center frequency'` (значение по умолчанию) | `'Quality factor and center frequency'` | `'Coefficients'`

`Пропускная способность` Пропускная способность на 3 дБ
`2205` (значение по умолчанию) | положительная скалярная величина

`CenterFrequency` — Отметьте или достигните максимума центральная частота
`11025` (значение по умолчанию) | положительная скалярная величина

`QualityFactor` — Добротность для метки или пикового фильтра
`5` (значение по умолчанию) | положительная скалярная величина

`SampleRate` — Частота дискретизации входа
`44100` (значение по умолчанию) | положительная скалярная величина

`BandwidthCoefficient` — Коэффициент пропускной способности
`0.72654` (значение по умолчанию) | действительный скаляр в области значений [-1 1]

`CenterFrequencyCoefficient` — Центральный коэффициент частоты
`0` (значение по умолчанию) | действительный скаляр в области значений [-1 1]

`x` Входной сигнал
вектор | матрица

`Yn` — Отметьте фильтруют вывод
вектор | матрица

`Yp` Достигните максимума выведенный фильтр
вектор | матрица