Exponenta Banner

iirparameq

БИХ biquad цифровой фильтр параметрического эквалайзера

свернуть все на странице

Функция iirparameq будет удалена в будущем релизе. Существующий код с помощью функции продолжает запускаться. Для нового кода используйте функцию designParamEQ от Audio Toolbox™ вместо этого.

Синтаксис

[SOS,SV] = iirparameq(N,G,Wo,BW)
[SOS,SV,B,A] = iirparameq(N,G,Wo,BW)

Описание

пример

[SOS,SV] = iirparameq(N,G,Wo,BW) возвращает коэффициенты БИХ порядка th N biquad цифровой параметрический эквалайзер с усилением G, центральная частота Wo и пропускная способность BW. Коэффициенты возвращены в матрице раздела второго порядка, SOS и векторе значений шкалы между каждым этапом biquad, SV.

пример

[SOS,SV,B,A] = iirparameq(N,G,Wo,BW) дополнительно возвращает матрицу разделов четвертого порядка числителя, B, и матричный A разделов четвертого порядка знаменателя, A. Они могут использоваться вместо biquad реализации и полезны для случая Wo = 0.5.

Примеры

свернуть все

Вычислите матрицу раздела второго порядка и значения шкалы параметрического эквалайзера.

[SOS,SV] = iirparameq(6,5,0.0042,0.0028)

SOS =

    1.0000   -1.9892    0.9894    1.0000   -1.9911    0.9912
    1.0000   -1.9926    0.9929    1.0000   -1.9941    0.9944
    1.0000   -1.9964    0.9965    1.0000   -1.9967    0.9968

SV =

    1.0009
    1.0000
    1.0009
    1.0000

Вычислите числитель и коэффициенты знаменателя разделов четвертого порядка параметрического эквалайзера.

[SOS,SV,B,A] = iirparameq(6,5,0.0042,0.0028)

SOS =

    1.0000   -1.9892    0.9894    1.0000   -1.9911    0.9912
    1.0000   -1.9926    0.9929    1.0000   -1.9941    0.9944
    1.0000   -1.9964    0.9965    1.0000   -1.9967    0.9968

SV =

    1.0009
    1.0000
    1.0009
    1.0000

B =

    1.0009   -1.9911    0.9903         0         0
    1.0009   -3.9927    5.9729   -3.9715    0.9903

A =

    1.0000   -1.9911    0.9912         0         0
    1.0000   -3.9908    5.9729   -3.9733    0.9912
Скрипт Open Live Script

Разработайте два эквалайзера, сосредоточенные на уровне 100 Гц и 1 000 Гц соответственно, и с усилением 5 дБ и с Q-фактором 1,5, для системы, достигающей 48 кГц.

Fs  = 48e3;
N   = 6;
G   = 5;
Q   = 1.5;
Wo1 = 100/(Fs/2);
Wo2 = 1000/(Fs/2);
% Obtain the bandwidth of the equalizers from the center frequencies and
% Q-factors.
BW1 = Wo1/Q;
BW2 = Wo2/Q;
% Design the equalizers and obtain their SOS and SV values.
[SOS1,SV1] = iirparameq(N,G,Wo1,BW1);  
[SOS2,SV2] = iirparameq(N,G,Wo2,BW2);

Разработайте фильтры biquad с помощью полученного SOS и значений SV.

BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1);
BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2,'ScaleValues',SV2);

Постройте ответ значения обоих фильтров с помощью логарифмической шкалы.

fvtool(BQ1,BQ2,'Fs',Fs,'FrequencyScale','Log');
legend('Equalizer centered at 100 Hz','Equalizer centered at 1000 Hz');

Скрипт Open Live Script

Разработайте метку восьмого порядка, фильтруют и сравнивают его с традиционным фильтром метки второго порядка, разработанным с IIRNOTCH. 

Fs  = 44.1e3;
N   = 8;
G   = -inf;
Q   = 1.8;
Wo  = 60/(Fs/2); % Notch at 60 Hz
BW  = Wo/Q; % Bandwidth occurs at -3 dB for this special case
[SOS1,SV1] = iirparameq(N,G,Wo,BW);  
[NUM,DEN]  = iirnotch(Wo,BW); 
SOS2 = [NUM,DEN];

Разработайте фильтры метки с помощью SOS и значений SV.

BQ1 = dsp.BiquadFilter('SOSMatrix',SOS1,'ScaleValues',SV1);
BQ2 = dsp.BiquadFilter('SOSMatrix',SOS2);

Постройте ответ значения обоих фильтров. Фильтры пересекаются в точке на-3 дБ.

FVT = fvtool(BQ1,BQ2,'Fs',Fs,'FrequencyScale','Log');
legend(FVT,'8th order notch filter','2nd order notch filter');

Входные параметры

свернуть все

Порядок параметрического эквалайзера, заданного как ровное положительное целое число.

Пример 6

Пример: 10

Типы данных: single | double

Усиление параметрического эквалайзера в дБ, заданном как действительный скаляр.

Пример 2

Пример: -2.2

Типы данных: single | double

Центральная частота параметрического эквалайзера, заданного как действительный скаляр в области значений [0.0 1.0]. Значение 1.0 соответствует π радианам/выборке.

Пример: 0.0

Пример: 1.0

Типы данных: single | double

Пропускная способность параметрического эквалайзера, заданного как действительный скаляр в области значений [0.0 1.0]. Значение 1.0 соответствует π радианам/выборке.

Пример: 0.0

Пример: 1.0

Типы данных: single | double

Выходные аргументы

свернуть все

Матрица раздела второго порядка, возвращенная как L с действительным знаком-by-6 матрица, где L является количеством разделов второго порядка фильтра.

Масштабируйте значения между каждым этапом biquad, возвращенным как вектор с действительным знаком длины L + 1.

Коэффициенты числителя разделов четвертого порядка параметрического эквалайзера, возвращенного как M с действительным знаком-by-5 матрица. M является количеством разделов четвертого порядка фильтра.

Коэффициенты знаменателя разделов четвертого порядка параметрического эквалайзера, возвращенного как M с действительным знаком-by-5 матрица. M является количеством разделов четвертого порядка фильтра.

Алгоритмы

свернуть все

Старший параметрический эквалайзер

Параметрические эквалайзеры являются цифровыми фильтрами, используемыми в обработке аудиоданных для корректировки содержимого частоты звукового сигнала. Параметрические эквалайзеры предусматривают возможности вне тех из графических эквалайзеров путем разрешения корректировки усиления, центральной частоты и пропускной способности каждого фильтра. Напротив, графические эквалайзеры допускают корректировку усиления каждого фильтра только. Цифровые параметрические аудио эквалайзеры обычно реализуются как биквадратное уравнение (БИХ второго порядка) фильтры. Из-за младшего разряда, биквадратные фильтры могут представить относительно большую пульсацию или области перехода. Когда несколько фильтров соединяются в каскаде, они могут наложиться друг с другом. При таких обстоятельствах предпочтены старшие фильтры. Старшие фильтры обеспечивают более плоские полосы пропускания, более резкие ребра полосы и больше управления формой каждого фильтра. Кроме того, если порядок фильтра устанавливается к два, конструктивные изменения к особому случаю: традиционный параметрический эквалайзер второго порядка.

Данные показывают ответ значения параметрического эквалайзера второго порядка по сравнению со старшим параметрическим эквалайзером.

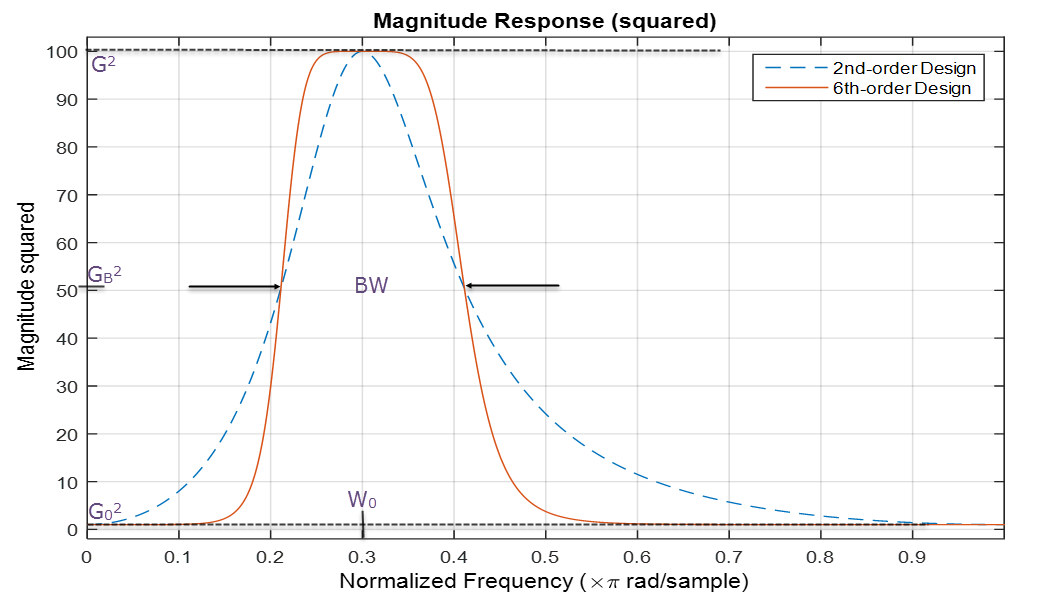
W0 = 0.3 × π радианы/выборка является центральной частотой эквалайзера, BW =, радианы/выборка 0.2 являются пропускной способностью эквалайзера, G =, 10 является пиковым усилением эквалайзера, G0 = 1 и GB = (G02 + G2) / 2.

Алгоритм

Первый шаг в проекте фильтра должен разработать старший аналог lowpass откладывающий фильтр, который соответствует заданному усилению и пропускной способности. Старший Фильтр Баттерворта используется с этой целью. Аналоговый Фильтр Баттерворта затем преобразовывается в цифровой lowpass, откладывающий фильтр, и наконец в худой эквалайзер, который сосредоточен на заданной пиковой частоте.

Спецификации проекта для цифрового эквалайзера являются порядком эквалайзера, N, усиления эквалайзера, G, центральной частоты эквалайзера, W0 и пропускной способности эквалайзера, BW.

Передаточной функцией старшего параметрического эквалайзера дают:

H(z)=[b00+b01z−1+b02z−21+a01z−1+a02z−2]r×∏i=1L[bi0+bi1z−1+bi2z−2+bi3z−3+bi4z−41+ai1z−1+ai2z−2+ai3z−3+ai4z−4]

где b00, b01, b02, a01 и a02 являются коэффициентами раздела второго порядка эквалайзера. bi0, bi1, bi2, bi3, bi4, ai1, ai2 и ai3 являются коэффициентами разделов четвертого порядка эквалайзера. L = (N –r) / 2, где r = 1, когда N нечетен, и r = 0, когда N ровен. Разделы четвертого порядка включены в разделы второго порядка так, чтобы можно было реализовать их использующий biquad фильтры.

Для получения дополнительной информации о том, как коэффициенты вычисляются с точки зрения спецификаций проекта, видят раздел "Butterworth Designs" в [1].

Ссылки

[1] Софокл Дж. Орфэнидис. "Старший Цифровой Проект Параметрического эквалайзера". J. Аудио Инженер Сок. Издание 53, ноябрь 2005, стр 1026–1046.

Смотрите также

| | |

Представленный в R2015a

Документация DSP System Toolbox
Поддержка