LMS адаптивные фильтры

Фильтр LMS вводные примеры

Этот раздел обеспечивает вводные примеры с помощью части наименьшее количество средних квадратичных (LMS) адаптивная функциональность фильтра в тулбоксе.

Тулбокс обеспечивает dsp.LMSFilter, который является Системой object™, который использует LMS-алгоритмы, чтобы искать оптимальное решение адаптивного фильтра. Поддержка объектов dsp.LMSFilter эти алгоритмы:

LMS-алгоритм, который решает уравнение Винера-Гопфа и находит коэффициенты фильтра для адаптивного фильтра
Нормированное изменение LMS-алгоритма
Изменение данных знака LMS-алгоритма, где исправление к весам фильтра в каждой итерации зависит от знака входа x (k)
Изменение ошибки знака LMS-алгоритма, где исправление применилось к текущим весам фильтра за каждую последовательную итерацию, зависит от знака ошибки, e (k)
Изменение знака знака LMS-алгоритма, где исправление применилось к текущим весам фильтра за каждую последовательную итерацию, зависит и от знака x (k) и от знака e (k).

Чтобы продемонстрировать сходства и различия среди различных LMS-алгоритмов, предоставленных в тулбоксе, LMS и адаптивные примеры фильтра NLMS используют тот же фильтр для неизвестной системы. Неизвестный фильтр является ограниченным фильтром lowpass от примеров fircband.

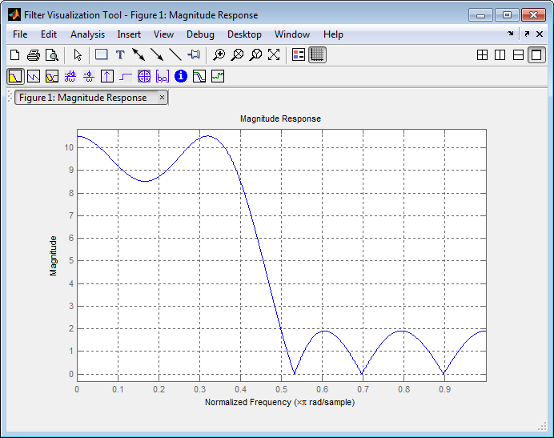
[b,err,res]=fircband(12,[0 0.4 0.5 1], [1 1 0 0], [1 0.2],... 
{'w' 'c'});
fvtool(b,1);

От фигуры вы видите, что фильтр действительно lowpass и ограничен к 0,2 пульсациям в полосе задерживания. С этим как базовая линия адаптивные примеры фильтра LMS используют адаптивные LMS-алгоритмы, чтобы идентифицировать, что это просачивается роль системы идентификации.

Чтобы рассмотреть общую модель для системного режима ID, посмотрите на System Identification для размещения.

Для изменений знака LMS-алгоритма примеры используют подавление помех в качестве демонстрационного приложения, в противоположность приложению системы идентификации, используемому в примерах LMS.

System Identification Используя LMS-алгоритм

Чтобы использовать адаптивные функции filter в тулбоксе, необходимо обеспечить три вещи:

Адаптивный LMS-алгоритм, чтобы использовать. Можно выбрать алгоритм по вашему выбору путем установки свойства Method dsp.LMSFilter к желаемому алгоритму.
Неизвестная система или процесс, чтобы адаптироваться к. В этом примере фильтр, разработанный fircband, является неизвестной системой.
Соответствующие входные данные, чтобы осуществить процесс адаптации. С точки зрения типичной модели LMS это желаемый сигнал d (k) и входной сигнал x (k).

Запустите путем определения входного сигнала x.

x = 0.1*randn(250,1);

Вход является широкополосным шумом. Для неизвестного системного фильтра используйте fircband, чтобы создать двенадцатый порядок lowpass фильтр:

[b,err,res] = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],{'w','c'});

Несмотря на то, что вам не нужны они здесь, включайте выходные аргументы res и err.

Теперь пропустите сигнал через неизвестную систему, чтобы получить желаемый сигнал.

d = filter(b,1,x);

С неизвестным разработанным фильтром и желаемый сигнал на месте вы создаете и применяете адаптивный объект фильтра LMS, чтобы идентифицировать неизвестное.

Подготовка адаптивного объекта фильтра требует, чтобы вы обеспечили начальные значения для оценок коэффициентов фильтра и размера шага LMS. Вы могли запустить с предполагаемых коэффициентов некоторого набора ненулевых значений; этот пример использует нули для 12 начальных весов фильтра. Установите свойство InitialConditions dsp.LMSFilter к желаемым начальным значениям весов фильтра.

Для размера шага, 0.8 рыночная стоимость — хороший компромисс между тем, чтобы быть достаточно большим, чтобы сходиться хорошо в этих 250 итерациях (250 входных точек выборки) и достаточно маленький, чтобы создать точную оценку неизвестного фильтра.

mu = 0.8;
lms = dsp.LMSFilter(13,'StepSize',mu,'WeightsOutputPort',true);

Наконец, с помощью объекта dsp.LMSFilter lms, желаемый сигнал, d и вход к фильтру, x, запускают адаптивный фильтр, чтобы определить неизвестную систему и построить результаты, сравнивая фактические коэффициенты от fircband до коэффициентов, найденных dsp.LMSFilter.

[y,e,w] = lms(x,d);
stem([b.' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual Filter Weights','Estimated Filter Weights',...
       'Location','NorthEast')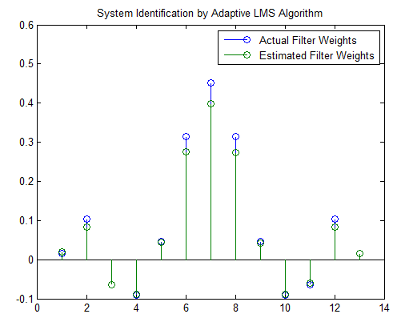

Как эксперимент, попытайтесь изменить размер шага на 0,2. Повторение примера с mu = 0.2 приводит к следующей диаграмме стебель-листья. Предполагаемым весам не удается аппроксимировать фактический вес тесно.

mu = 0.2;
lms = dsp.LMSFilter(13,'StepSize',mu,'WeightsOutputPort',true);
[y,e,w] = lms(x,d);
stem([b.' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual Filter Weights','Estimated Filter Weights',...
       'Location','NorthEast')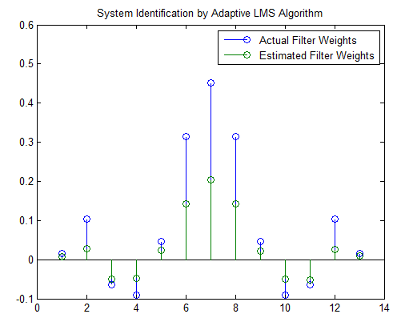

Поскольку это может быть то, потому что вы не выполнили итерации по LMS-алгоритму достаточно раз, попытайтесь использовать 1 000 выборок. С 1 000 выборок диаграмма стебель-листья, показанная в следующей фигуре, выглядит намного лучше, хотя за счет намного большего количества вычисления. Очевидно необходимо заботиться, чтобы выбрать размер шага и с требуемым вычислением и с точностью предполагаемого фильтра в памяти.

for index = 1:4
  x = 0.1*randn(250,1);
  d = filter(b,1,x);
  [y,e,w] = lms(x,d);
end
stem([b.' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual Filter Weights','Estimated Filter Weights',...
       'Location','NorthEast')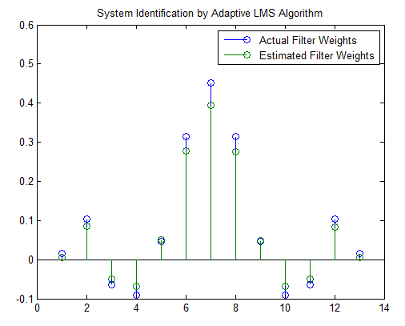

System Identification Используя нормированный LMS-алгоритм

Чтобы улучшать производительность сходимости LMS-алгоритма, нормированный вариант (NLMS) использует адаптивный размер шага на основе степени сигнала. Когда степень входного сигнала изменяется, алгоритм вычисляет входную мощность и настраивает размер шага, чтобы поддержать соответствующее значение. Таким образом размер шага изменяется со временем.

В результате нормированный алгоритм сходится более быстро с меньшим количеством выборок во многих случаях. Для входных сигналов, которые изменяются медленно в зависимости от времени, нормированный LMS может представлять более эффективный подход LMS.

В нормированном примере LMS-алгоритма вы использовали fircband, чтобы создать фильтр, который вы идентифицируете. Таким образом, можно сравнить результаты, вы используете тот же фильтр и устанавливаете свойство Method на dsp.LMSFilter к 'Normalized LMS'. использовать нормированное изменение LMS-алгоритма. Необходимо видеть лучшую сходимость с подобной точностью.

Во-первых, сгенерируйте входной сигнал и неизвестный фильтр.

x = 0.1*randn(500,1);
[b,err,res] = fircband(12,[0 0.4 0.5 1], [1 1 0 0], [1 0.2],... 
{'w' 'c'});
d = filter(b,1,x);

Снова d представляет желаемый сигнал d (x), когда вы задали его ранее, и b содержит коэффициенты фильтра для вашего неизвестного фильтра.

lms = dsp.LMSFilter(13,'StepSize',mu,'Method',...
   'Normalized LMS','WeightsOutputPort',true);

Вы используете предыдущий код, чтобы инициализировать нормированный LMS-алгоритм. Для получения дополнительной информации о дополнительных входных параметрах, обратитесь к dsp.LMSFilter.

Выполнение процесса системы идентификации является вопросом использования объекта dsp.LMSFilter с желаемым сигналом, входным сигналом, и начальными коэффициентами фильтра и условиями, заданными в s как входные параметры. Затем постройте результаты сравнить адаптированный фильтр с фактическим фильтром.

[y,e,w] = lms(x,d);
stem([b.' w])
title('System Identification by Normalized LMS Algorithm')
legend('Actual Filter Weights','Estimated Filter Weights',...
       'Location','NorthEast')

Как показано в следующей диаграмме стебель-листья (удобный способ сравнить предполагаемые и фактические коэффициенты фильтра), эти два почти идентичны.

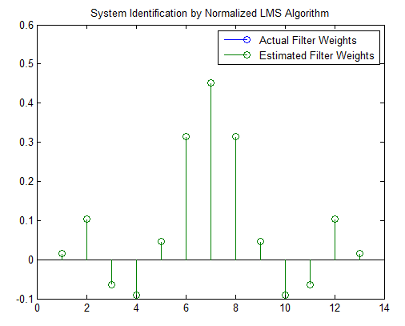
Если вы сравниваете производительность сходимости регулярного LMS-алгоритма к нормированному варианту LMS, вы видите, что нормированная версия адаптируется в гораздо меньшем количестве итераций к результату, почти столь же хорошему как ненормированная версия.

lms_normalized = dsp.LMSFilter(13,'StepSize',mu,...
    'Method','Normalized LMS','WeightsOutputPort',true);
lms_nonnormalized = dsp.LMSFilter(13,'StepSize',mu,...
    'Method','LMS','WeightsOutputPort',true);
[~,e1,~] = lms_normalized(x,d);
[~,e2,~] = lms_nonnormalized(x,d);
plot([e1,e2]);
title('Comparing the LMS and NLMS Conversion Performance');
legend('NLMS Derived Filter Weights', ...
       'LMS Derived Filter Weights','Location', 'NorthEast');

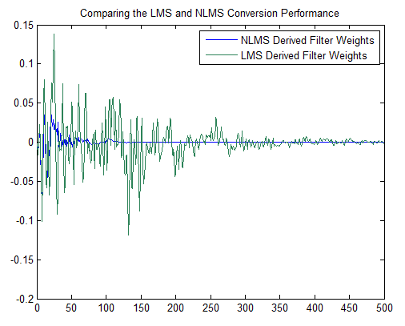
Подавление помех Используя LMS-алгоритм данных знака

Когда объем вычисления, требуемого выводить адаптивный фильтр, управляет вашим процессом разработки, вариант данных знака LMS (SDLMS) алгоритм может быть очень хорошим выбором, как продемонстрировано в этом примере.

К счастью, текущее состояние проекта цифрового сигнального процессора (DSP) ослабило потребность минимизировать количество операций путем создания DSPS, чей умножаются, и операции сдвига состоят в том с такой скоростью, как добавляют операции. Таким образом часть импульса для алгоритма данных знака (и ошибка знака и изменения знака знака) была потеряна технологическим улучшениям DSP.

В стандартных и нормированных изменениях адаптивного фильтра LMS коэффициенты для адаптирующегося фильтра являются результатом среднеквадратичной погрешности между желаемым сигналом и выходным сигналом неизвестной системы. Используя данные знака алгоритм изменяет вычисление среднеквадратичной погрешности при помощи знака входных данных изменить коэффициенты фильтра.

Когда ошибка положительна, новые коэффициенты являются предыдущими коэффициентами плюс ошибка, умноженная на размер шага µ. Если ошибка отрицательна, новые коэффициенты являются снова предыдущими коэффициентами минус ошибка, умноженная на µ — обращают внимание на изменения знака.

Когда вход является нулем, новые коэффициенты совпадают с предыдущим набором.

В векторной форме LMS-алгоритм данных знака

$\begin{matrix} w (k + 1) = w (k) + μ e (k) sgn [x (k)], \\ sgn [x (k)] = {\begin{cases} 1, x (k) > \\ 00, x (k) = 0 \\ - 1, x (k) < 0 \end{cases} \end{matrix}$

Когда вы задаете меньший mu, исправление к весам фильтра становится меньшим для каждой выборки, и ошибка SDLMS падает более медленно. Больший mu изменяет веса больше для каждого шага, таким образом, ошибка падает более быстро, но получившаяся ошибка не приближается к идеальному решению как тесно. Чтобы гарантировать хороший уровень сходимости и устойчивость, выберите mu в следующих практических границах

$0 < μ < \frac{1}{N {I n p u t S i g n a l P o w e r}}$

где N является количеством выборок в сигнале. Кроме того, задайте mu как степень двойки для эффективного вычисления.

Примечание

Как вы устанавливаете начальные условия алгоритма данных знака, глубоко влияет на эффективность адаптации. Поскольку алгоритм по существу квантует входной сигнал, алгоритм может стать нестабильным легко.

Серия больших входных значений, вместе с процессом квантования может привести к ошибке при росте вне всех границ. Вы ограничиваете тенденцию алгоритма данных знака выйти из-под контроля путем выбора размера небольшого шага (µ <<1) и устанавливания начальных условий для алгоритма к ненулевым положительным и отрицательным величинам.

В этом примере подавления помех, свойстве dsp.LMSFilter Method набора к 'Sign-Data LMS'. Этот пример требует двух наборов входных данных:

Данные, содержащие сигнал, повреждаются шумом. В Использовании Адаптивного Фильтра, чтобы Удалить Шум из Неизвестной Системы, это - d (k), желаемый сигнал. Процесс подавления помех удаляет шум, оставляя сигнал.
Данные, содержащие случайный шум (x (k) в Использовании Адаптивного Фильтра, чтобы Удалить Шум из Неизвестной Системы), который коррелируется с шумом, который повреждает данные сигнала. Без корреляции между шумовыми данными адаптирующийся алгоритм не может удалить шум из сигнала.

Для сигнала используйте синусоиду. Обратите внимание на то, что signal является вектор-столбцом 1 000 элементов.

signal = sin(2*pi*0.055*[0:1000-1]');

Теперь, добавьте коррелируемый белый шум в signal. Чтобы гарантировать, что шум коррелируется, передайте шум через lowpass КИХ-фильтр, и затем добавьте отфильтрованный шум в сигнал.

noise = randn(1000,1);
nfilt = fir1(11,0.4); % Eleventh order lowpass filter
fnoise = filter(nfilt,1,noise); % Correlated noise data
d = signal + fnoise;

fnoise является коррелированым шумом, и d является теперь желаемым входом к алгоритму данных знака.

В System Identification Используя LMS-алгоритм вы создали фильтр по умолчанию, который устанавливает коэффициенты фильтра на нули. В большинстве случаев тот подход не работает на алгоритм данных знака. Чем ближе вы устанавливаете свои начальные коэффициенты фильтра на ожидаемые значения, тем более вероятно случается так, что алгоритм остается хорошего поведения и сходится к решению для фильтра, которое удаляет шум эффективно.

В данном примере запустите с коэффициентов в фильтре, вы раньше фильтровали шум (nfilt) и изменяли их немного, таким образом, алгоритм должен адаптироваться.

coeffs = nfilt.' -0.01; % Set the filter initial conditions.
mu = 0.05;          % Set the step size for algorithm updating.

С необходимыми входными параметрами для подготовленного dsp.LMSFilter создайте объект фильтра LMS, запустите адаптацию и просмотрите результаты.

lms = dsp.LMSFilter(12,'Method','Sign-Data LMS',...
   'StepSize',mu,'InitialConditions',coeffs);
[~,e] = lms(noise,d);
L = 200;
plot(0:L-1,signal(1:L),0:L-1,e(1:L));
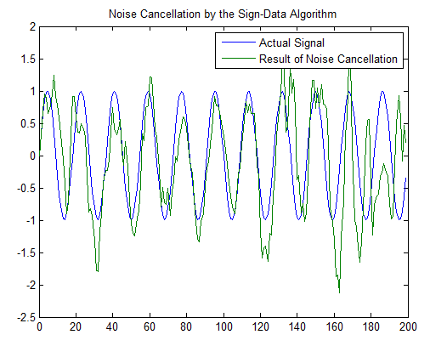
title('Noise Cancellation by the Sign-Data Algorithm');
legend('Actual Signal','Result of Noise Cancellation',...
       'Location','NorthEast');

Когда dsp.LMSFilter запускается, он использует, гораздо меньше умножает операции, чем любой из LMS-алгоритмов. Кроме того, выполнение адаптации данных знака требует, чтобы только битная перемена умножилась, когда размер шага является степенью двойки.

Несмотря на то, что производительность алгоритма данных знака как показано в следующей фигуре довольно хороша, алгоритм данных знака намного менее стабилен, чем стандартные изменения LMS. В этом примере подавления помех сигнал после того, как обработка является очень хорошим соответствием к входному сигналу, но алгоритм мог очень легко вырасти без связанного, а не достигнуть хорошей производительности.

Изменяя InitialConditions, mu, или даже lowpass фильтруют вас, раньше создавал коррелированый шум, может заставить подавление помех перестать работать и алгоритм, чтобы стать бесполезным.

Подавление помех Используя LMS-алгоритм ошибки знака

В некоторых случаях вариант ошибки знака LMS-алгоритма (SELMS) может быть очень хорошим выбором для адаптивного приложения фильтра.

В стандартных и нормированных изменениях адаптивного фильтра LMS коэффициенты для адаптирующегося фильтра являются результатом вычисления среднеквадратичной погрешности между желаемым сигналом и выходным сигналом неизвестной системы и применением результата к текущим коэффициентам фильтра. Используя ошибку знака алгоритм заменяет вычисление среднеквадратичной погрешности при помощи знака ошибки изменить коэффициенты фильтра.

В векторной форме LMS-алгоритм ошибки знака

$\begin{matrix} w (k + 1) = w (k) + μ sgn [e (k)] [x (k)], \\ sgn [e (k)] = {\begin{cases} 1, e (k) > \\ 00, e (k) = 0 \\ - 1, e (k) < 0 \end{cases}} \end{matrix}$

с вектором w содержащий веса применился к коэффициентам фильтра и вектору x содержащий входные данные. e (k) (равный желаемому сигналу - отфильтрованный сигнал) ошибка во время k и количество, которое алгоритм SELMS стремится минимизировать. µ (mu) является размером шага. Когда вы задаете меньший mu, исправление к весам фильтра становится меньшим для каждой выборки, и ошибка SELMS падает более медленно.

Больший mu изменяет веса больше для каждого шага, таким образом, ошибка падает более быстро, но получившаяся ошибка не приближается к идеальному решению как тесно. Чтобы гарантировать хороший уровень сходимости и устойчивость, выберите mu в следующих практических границах

$0 < μ < \frac{1}{N {I n p u t S i g n a l P o w e r}}$

Примечание

Как вы устанавливаете начальные условия алгоритма данных знака, глубоко влияет на эффективность адаптации. Поскольку алгоритм по существу квантует сигнал ошибки, алгоритм может стать нестабильным легко.

Серия больших ошибочных значений, вместе с процессом квантования может привести к ошибке при росте вне всех границ. Вы ограничиваете тенденцию алгоритма ошибки знака выйти из-под контроля путем выбора размера небольшого шага (µ<< 1) и устанавливания начальных условий для алгоритма к ненулевым положительным и отрицательным величинам.

В этом примере подавления помех объект dsp.LMSFilter требует двух наборов входных данных:

Данные, содержащие сигнал, повреждаются шумом. В Использовании Адаптивного Фильтра, чтобы Удалить Шум из Неизвестной Системы, это - d (k), желаемый сигнал. Процесс подавления помех удаляет шум, оставляя сигнал.
Данные, содержащие случайный шум (x (k) в Использовании Адаптивного Фильтра, чтобы Удалить Шум из Неизвестной Системы), который коррелируется с шумом, который повреждает данные сигнала. Без корреляции между шумовыми данными адаптирующийся алгоритм не может удалить шум из сигнала.

Для сигнала используйте синусоиду. Обратите внимание на то, что signal является вектор-столбцом 1 000 элементов.

signal = sin(2*pi*0.055*[0:1000-1]');

Теперь, добавьте коррелируемый белый шум в signal. Чтобы гарантировать, что шум коррелируется, передайте шум через lowpass КИХ-фильтр, затем добавьте отфильтрованный шум в сигнал.

noise = randn(1000,1);
nfilt = fir1(11,0.4); % Eleventh order lowpass filter.
fnoise = filter(nfilt,1,noise); % Correlated noise data.
d = signal + fnoise;

fnoise является коррелированым шумом, и d является теперь желаемым входом к алгоритму данных знака.

Чтобы подготовить объект dsp.LMSFilter к обработке, установите начальные условия веса (InitialConditions) и mu (StepSize) для объекта. Как отмечено ранее в этом разделе, значения вы устанавливаете для coeffs, и mu определяют, может ли адаптивный фильтр удалить шум из пути прохождения сигнала. В System Identification Используя LMS-алгоритм вы создали фильтр по умолчанию, который устанавливает коэффициенты фильтра на нули.

Обнуление коэффициентов часто не работает на алгоритм ошибки знака. Чем ближе вы устанавливаете свои начальные коэффициенты фильтра на ожидаемые значения, тем более вероятно случается так, что алгоритм остается хорошего поведения и сходится к решению для фильтра, которое удаляет шум эффективно.

В данном примере вы запускаете с коэффициентов в фильтре, вы раньше фильтровали шум (nfilt) и изменяли их немного, таким образом, алгоритм должен адаптироваться.

coeffs = nfilt.' -0.01; % Set the filter initial conditions.
mu = 0.05;            % Set step size for algorithm update.

С необходимыми входными параметрами для подготовленного dsp.LMSFilter запустите адаптацию и просмотрите результаты.

lms = dsp.LMSFilter(12,'Method','Sign-Error LMS',...
   'StepSize',mu,'InitialConditions',coeffs);
[~,e] = lms(noise,d);
L = 200;
plot(0:199,signal(1:200),0:199,e(1:200));
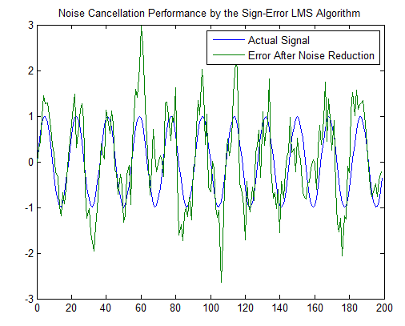
title('Noise Cancellation Performance by the Sign-Error LMS Algorithm');
legend('Actual Signal','Error After Noise Reduction',...
       'Location','NorthEast')

Когда LMS-алгоритм ошибки знака запускается, он использует, гораздо меньше умножает операции, чем любой из LMS-алгоритмов. Кроме того, выполнение адаптации ошибки знака требует, чтобы только битная перемена умножилась, когда размер шага является степенью двойки.

Несмотря на то, что производительность алгоритма данных знака как показано в следующей фигуре довольно хороша, алгоритм данных знака намного менее стабилен, чем стандартные изменения LMS. В этом примере подавления помех сигнал после того, как обработка является очень хорошим соответствием к входному сигналу, но алгоритм мог очень легко стать нестабильным, а не достигнуть хорошей производительности.

При изменении начальных условий веса (InitialConditions) и mu (StepSize), или даже lowpass фильтруют вас, раньше создавал коррелированый шум, может заставить подавление помех перестать работать и алгоритм, чтобы стать бесполезным.

Подавление помех Используя LMS-алгоритм знака знака

Еще одним примером изменения LMS-алгоритма в тулбоксе является вариант знака знака (SSLMS). Объяснение для этой версии совпадает с теми для данных знака и алгоритмов ошибки знака, представленных в предыдущих разделах. Для получения дополнительной информации обратитесь к Подавлению помех Используя LMS-алгоритм Данных Знака.

Алгоритм знака знака (SSLMS) заменяет вычисление среднеквадратичной погрешности на использование знака входных данных изменить коэффициенты фильтра. Когда ошибка положительна, новые коэффициенты являются предыдущими коэффициентами плюс ошибка, умноженная на размер шага µ.

Если ошибка отрицательна, новые коэффициенты являются снова предыдущими коэффициентами минус ошибка, умноженная на µ — обращают внимание на изменения знака. Когда вход является нулем, новые коэффициенты совпадают с предыдущим набором.

В сущности алгоритм квантует и ошибку и вход путем применения оператора знака к ним.

В векторной форме LMS-алгоритм знака знака

$\begin{matrix} w (k + 1) = w (k) + μ sgn [e (k)] sgn [x (k)], \\ sgn [z (k)] = {\begin{cases} 1, z (k) > \\ 00, z (k) = 0 \\ - 1, z (k) < 0 \end{cases} \end{matrix}$

где

$z (k) = [e (k)] sgn [x (k)]$

Вектор w содержит веса, применился к коэффициентам фильтра, и вектор x содержит входные данные. e (k) ( = желаемый сигнал - отфильтрованный сигнал) ошибка во время k и количество, которое алгоритм SSLMS стремится минимизировать. µ (mu) является размером шага. Когда вы задаете меньший mu, исправление к весам фильтра становится меньшим для каждой выборки, и ошибка SSLMS падает более медленно.

$0 < μ < \frac{1}{N {I n p u t S i g n a l P o w e r}}$

Примечание

Как вы устанавливаете начальные условия алгоритма знака знака, глубоко влияет на эффективность адаптации. Поскольку алгоритм по существу квантует входной сигнал и сигнал ошибки, алгоритм может стать нестабильным легко.

Серия больших ошибочных значений, вместе с процессом квантования может привести к ошибке при росте вне всех границ. Вы ограничиваете тенденцию алгоритма знака знака выйти из-под контроля путем выбора размера небольшого шага (µ<< 1) и устанавливания начальных условий для алгоритма к ненулевым положительным и отрицательным величинам.

В этом примере подавления помех объект dsp.LMSFilter требует двух наборов входных данных:

Данные, содержащие сигнал, повреждаются шумом. В Использовании Адаптивного Фильтра, чтобы Удалить Шум из Неизвестной Системы, это - d (k), желаемый сигнал. Процесс подавления помех удаляет шум, оставляя убранный сигнал как содержимое сигнала ошибки.
Данные, содержащие случайный шум (x (k) в Использовании Адаптивного Фильтра, чтобы Удалить Шум из Неизвестной Системы), который коррелируется с шумом, который повреждает данные сигнала, названные. Без корреляции между шумовыми данными адаптирующийся алгоритм не может удалить шум из сигнала.

Для сигнала используйте синусоиду. Обратите внимание на то, что signal является вектор-столбцом 1 000 элементов.

signal = sin(2*pi*0.055*[0:1000-1]');

noise = randn(1000,1);
nfilt = fir1(11,0.4); % Eleventh order lowpass filter
fnoise = filter(nfilt,1,noise); % Correlated noise data
d = signal + fnoise;

fnoise является коррелированым шумом, и d является теперь желаемым входом к алгоритму данных знака.

Чем ближе вы устанавливаете свои начальные коэффициенты фильтра на ожидаемые значения, тем более вероятно случается так, что алгоритм остается хорошего поведения и сходится к решению для фильтра, которое удаляет шум эффективно. В данном примере вы запускаете с коэффициентов в фильтре, вы раньше фильтровали шум (nfilt) и изменяли их немного, таким образом, алгоритм должен адаптироваться.

coeffs = nfilt.' -0.01; % Set the filter initial conditions.
mu = 0.05;          % Set the step size for algorithm updating.

lms = dsp.LMSFilter(12,'Method','Sign-Sign LMS',...
   'StepSize',mu,'InitialConditions',coeffs);
[~,e] = lms(noise,d);
L = 200;
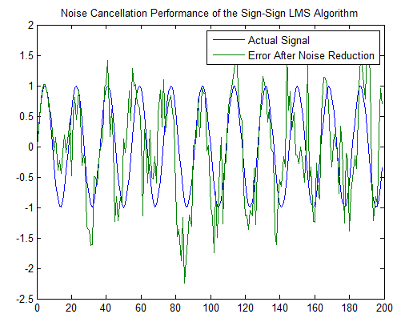
plot(0:199,signal(1:200),0:199,e(1:200));
title('Noise Cancellation Performance by the Sign-Error LMS Algorithm');
legend('Actual Signal','Error After Noise Reduction',...
       'Location','NorthEast')

Когда dsp.LMSFilter запускается, он использует, гораздо меньше умножает операции, чем любой из LMS-алгоритмов. Кроме того, выполнение адаптации знака знака требует, чтобы только битная перемена умножилась, когда размер шага является степенью двойки.

Несмотря на то, что производительность алгоритма знака знака как показано в следующей фигуре довольно хороша, алгоритм знака знака намного менее стабилен, чем стандартные изменения LMS. В этом примере подавления помех сигнал после того, как обработка является очень хорошим соответствием к входному сигналу, но алгоритм мог очень легко стать нестабильным, а не достигнуть хорошей производительности.

Как в стороне, LMS-алгоритм знака знака является частью международного стандарта CCITT для телефонии ADPCM на 32 Кбит/с.

Ссылки

[1] Hayes, Монсон Х., статистическая цифровая обработка сигналов и Modeling, John Wiley & Sons, 1996, 493–552.

[2] Haykin, Саймон, адаптивная теория фильтра, Prentice-Hall, Inc., 1996

Документация