Нечеткий вывод является процессом формулировки отображения от данного входа до вывода с помощью нечеткой логики. Отображение затем обеспечивает основание, от которого решения могут быть приняты, или различаемые шаблоны. Процесс нечеткого вывода включает все части, которые описаны в Функциях принадлежности, Логических операциях, и Если затем Правила.
В этом разделе описываются нечеткий процесс вывода и использует пример 2D входа, проблемы добавления подсказки с тремя правилами, с одним выходом от Основной проблемы Добавления подсказки. Базовую структуру этого примера показывают в следующей схеме:
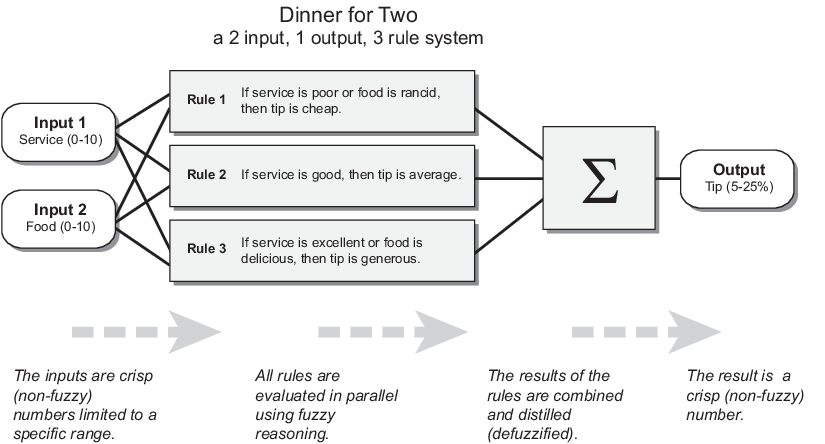
Информационные потоки слева направо, от двух входных параметров до одного вывода. Параллельная природа правил является важным аспектом систем нечеткой логики. Вместо резкого переключения между режимами на основе точек останова логика течет гладко из областей, где одно правило или другой доминируют.
Нечеткий процесс вывода включает пять частей:
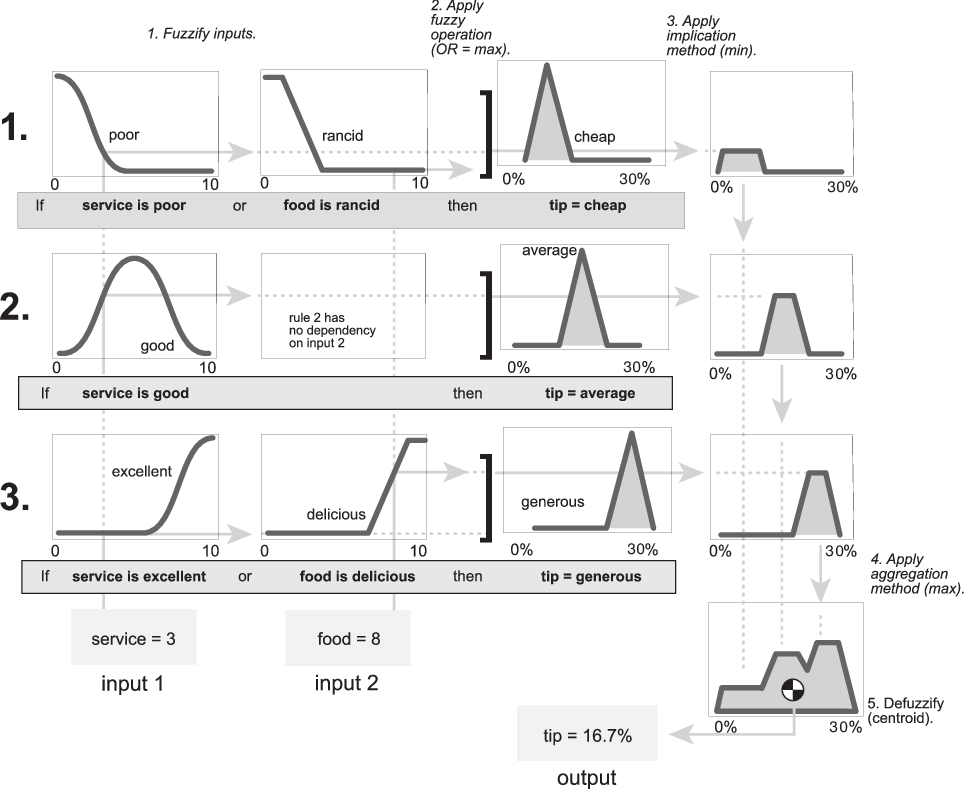
Нечеткая схема вывода отображает все части нечеткого процесса вывода — от размывания до defuzzification.
Первый шаг должен взять входные параметры и определить степень, до которой они принадлежат каждому из соответствующих нечетких множеств через функции принадлежности. В программном обеспечении Fuzzy Logic Toolbox™ вход всегда является четким численным значением, ограниченным вселенной беседы о входной переменной (в этом случае, интервал от 0 до 10). Вывод является нечеткой степенью членства в квалифицирующем лингвистическом наборе (всегда интервал от 0 до 1). Размывание входа составляет или поиск по таблице или функциональную оценку.
Этот пример основан на трех правилах, и каждое из правил зависит от решения входных параметров в несколько различных нечетких лингвистических наборов: сервис плох, сервис хорош, еда является прогорклой, еда восхитительна и так далее. Прежде чем правила могут быть оценены, входные параметры должны быть fuzzified согласно каждому из этих лингвистических наборов. Например, до какой степени еда восхитительна? Следующие данные показывают, как хорошо еда в гипотетическом ресторане (оцененный в шкале от 0 до 10) квалифицирует как лингвистическая переменная восхитительное использование функции принадлежности. В этом случае мы оцениваем еду как 8, которая, учитывая графическое определение восхитительных, соответствует µ = 0.7 для восхитительной функции принадлежности.
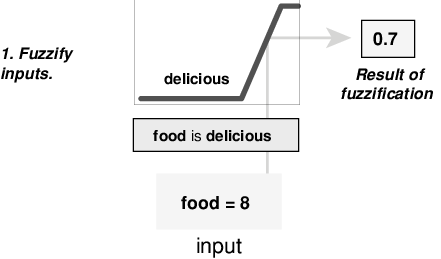
Этим способом каждый вход является fuzzified по всем функциям принадлежности квалификации, требуемым правилами.
После того, как входные параметры являются fuzzified, вы знаете степень, до которой каждая часть антецедента удовлетворена для каждого правила. Если антецедент правила имеет больше чем одну часть, нечеткий оператор применяется, чтобы получить один номер, который представляет результат антецедента правила. Этот номер затем применяется к выходной функции. Вход к нечеткому оператору является двумя или больше значениями членства от fuzzified входных переменных. Вывод является одним значением истинности.
Как описан в разделе Logical Operations, любое количество четко определенных методов может заполнить для операции И или операции OR. В тулбоксе поддерживаются два встроенных метода AND: min (минимум) и напоминание (продукт). Два встроенных метода OR также поддержаны: макс. (максимум) и вероятностный метод OR про-Бор. Вероятностный метод OR (также известный как алгебраическую сумму) вычисляется согласно уравнению:
| про-Бор (a, b) = + b - ab |
В дополнение к этим встроенным методам можно создать собственные методы для AND и OR пишущий любую функцию и устанавливая это быть предпочтительным методом.
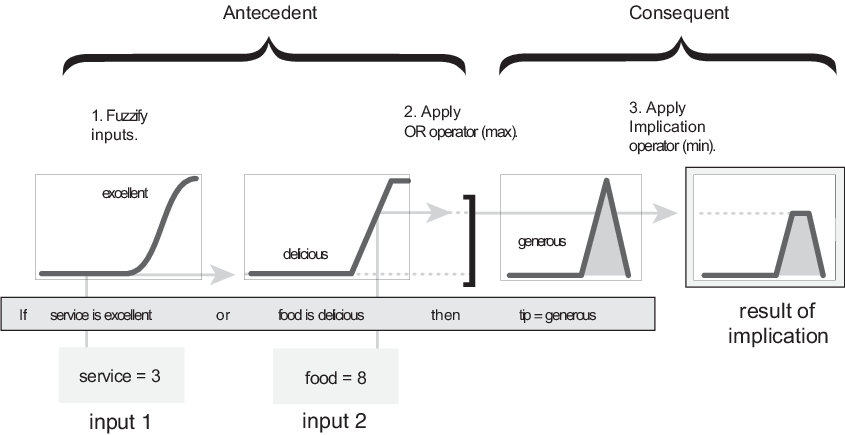
Следующие данные показывают операцию ИЛИ макс. на работе, оценивая антецедент правила 3 для вычисления добавления подсказки. Две различных части антецедента (сервис превосходен и еда, восхитительны), привел к нечетким значениям членства 0.0 и 0.7 соответственно. Нечеткая операция ИЛИ просто выбирает максимум этих двух значений, 0.7, и нечеткая операция для правила 3 завершена. Вероятностный метод OR все еще привел бы к 0,7.
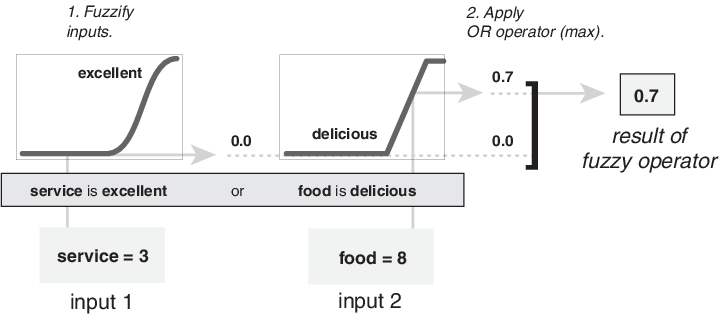
Прежде, чем применить метод значения, необходимо определить вес правила. Каждое правило имеет вес (номер от 0 до 1), который применяется к номеру, данному антецедентом. Обычно этот вес равняется 1 (как это для этого примера), и таким образом не имеет никакого эффекта на процесс значения. Однако можно уменьшить эффект одного правила относительно других путем изменения его значения веса на что-то другое, чем 1.
После того, как соответствующее взвешивание было присвоено каждому правилу, метод значения реализован. Следствие является нечетким множеством, представленным функцией принадлежности, который веса соответственно лингвистические характеристики, которые приписаны ему. Следствие изменено с помощью функции, сопоставленной с антецедентом (один номер). Вход для процесса значения является одним номером, данным антецедентом, и вывод является нечетким множеством. Значение реализовано для каждого правила. Поддерживаются два встроенных метода, и они - те же функции, которые используются методом AND: min (минимум), который обрезает выходное нечеткое множество и напоминание (продукт), который масштабирует выходное нечеткое множество.
Системы Sugeno всегда используют метод значения продукта.
Поскольку решения основаны на тестировании всех правил в FIS, правила, выходные параметры должны быть объединены некоторым способом. Агрегация является процессом, который нечеткие множества, которые представляют выходные параметры каждого правила, объединены в одно нечеткое множество. Агрегация только происходит однажды для каждой выходной переменной, которая является перед финалом defuzzification шаг. Вход процесса агрегации является списком усеченных выходных функций, возвращенных процессом значения для каждого правила. Вывод процесса агрегации является одним нечетким множеством для каждой выходной переменной.
Пока метод агрегации является коммутативным, затем порядок, в котором выполняются правила, неважен. Поддерживаются три встроенных метода:
max (максимум)
probor (вероятностный OR)
sum (сумма правила вывела наборы),
В следующей схеме все три правила отображены, чтобы показать, как правило, выходные параметры агрегированы в одно нечеткое множество, функция принадлежности которого присваивает взвешивание для каждого вывода (совет) значение.
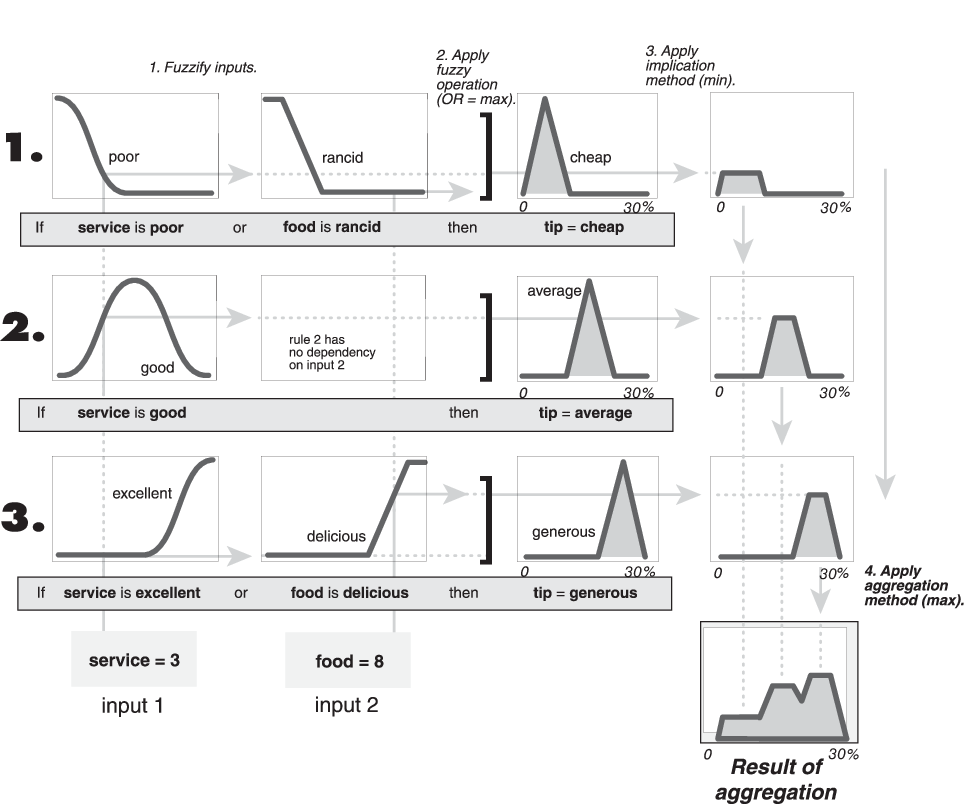
Системы Sugeno всегда используют метод агрегации sum.
Вход для defuzzification процесса является нечетким множеством (совокупное выходное нечеткое множество), и вывод является одним номером. Так, как нечеткость помогает оценке правила во время промежуточных шагов, финал желал, чтобы вывод для каждой переменной обычно был одним номером. Однако агрегат нечеткого множества охватывает область значений выходных значений, и так должен быть defuzzified, чтобы получить одно выходное значение из набора.
Существует пять встроенных defuzzification поддерживаемых методов: центроид, биссектриса, середина максимума (среднее значение максимального значения выходного набора), самый большой из максимума и самый маленький из максимума. Возможно, самый популярный defuzzification метод является центроидным вычислением, которое возвращает центр области под кривой, как показано в следующем:
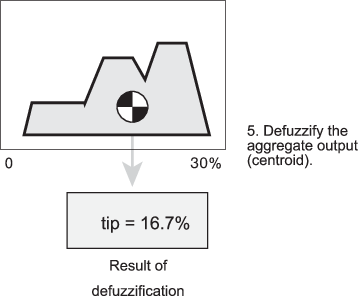
В то время как совокупное выходное нечеткое множество покрывает диапазон от 0%, хотя 30%, defuzzified значение между 5% и 25%. Эти пределы соответствуют центроидам cheap и функций принадлежности generous, соответственно.
Нечеткая схема вывода является составным объектом всех меньших схем, представленных до сих пор в этом разделе. Это одновременно отображает все части нечеткого процесса вывода, который вы исследовали. Информационные потоки через нечеткий вывод схематически изображают как показано в следующей фигуре.
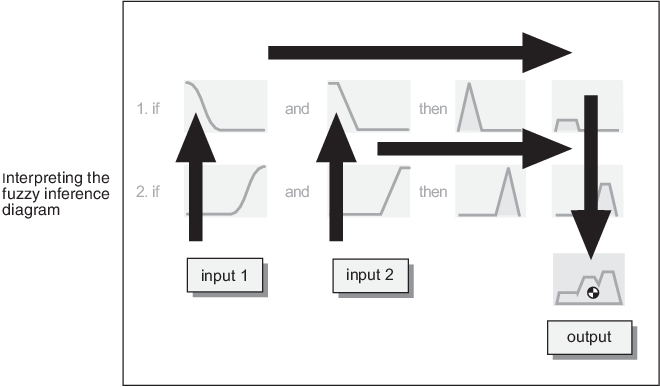
В этой фигуре поток проистекает из входных параметров в нижнем левом углу через каждую строку, и затем вниз правило выходные параметры в нижнем правом углу. Этот компактный поток показывает все целиком от размывания лингвистической переменной полностью через defuzzification совокупного вывода.
Следующие данные показывают фактическую полноразмерную нечеткую схему вывода. Используя нечеткую схему вывода, можно узнать много о том, как система действует. Например, для конкретных входных параметров в этой схеме, вы видите, что метод значения является усечением с функцией min. Макс. функция используется для нечеткой операции OR. Правило 3 (самая нижняя строка в схеме, показанной ранее), имеет самое сильное влияние на вывод. Средство просмотра Правила, описанное в Средстве просмотра Правила, является реализацией нечеткой схемы вывода.