gamultiobjВ этом разделе описываются алгоритм что использование gamultiobj, чтобы создать набор точек на передней стороне Парето. gamultiobj использует управляемый, элитарный генетический алгоритм (вариант NSGA-II [3]). Элитарный GA всегда способствует людям с лучшим значением фитнеса (ранг). Управляемый элитарный GA также способствует людям, которые могут помочь увеличить разнообразие генеральной совокупности, даже если у них есть более низкое значение фитнеса.
Большая часть терминологии для алгоритма gamultiobj совпадает с Терминологией Генетического алгоритма. Однако существуют некоторые дополнительные условия, описанные в этом разделе. Для получения дополнительной информации о терминологии и алгоритме, смотрите Деб [3].
Dominance — Точка x доминирует над точкой y для целевой функции с векторным знаком f когда:
fi (x) ≤ fi (y) для всего i.
fj (x) <fj (y) для некоторого j.
Термин "доминир" эквивалентен термину "нижний": x доминирует над y точно, когда y является нижним к x.
nondominated set среди набора точек, P является набором точек Q в P, которые не являются во власти никакой точки в P.
Ранг — Для выполнимых людей, существует итеративное определение ранга человека. Займите место 1 человек не во власти никаких других людей. Займите место над 2 людьми доминирует только ранг 1 человек. В целом займите место, над людьми k доминируют только люди в ранге k - 1 или ниже.
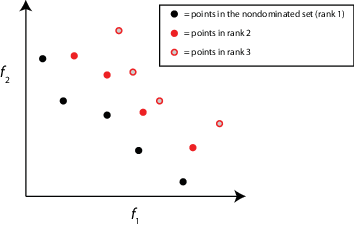
У людей с более низким рангом есть более высокий шанс выбора (более низкий ранг лучше).
У всех неосуществимых людей есть худший ранг, чем какой-либо выполнимый человек. В неосуществимой генеральной совокупности ранг является порядком отсортированной мерой по infeasibility плюс самый высокий ранг для выполнимых участников.
gamultiobj использует ранг, чтобы выбрать родительские элементы.
При давке Расстояния — толпящееся расстояние является мерой близости человека ее самым близким соседям. Алгоритм gamultiobj измеряет расстояние среди людей того же ранга. По умолчанию алгоритм измеряет расстояние на пробеле целевой функции. Однако можно измерить расстояние на пробеле переменной решения (также названный пробелом переменной проекта) путем установки опции DistanceMeasureFcn на {@distancecrowding,'genotype'}.
Алгоритм устанавливает расстояние людей в крайних положениях к Inf. Для остающихся людей алгоритм вычисляет расстояние как сумму по размерностям нормированных абсолютных расстояний между отсортированными соседями человека. Другими словами, для размерности m и отсортированный, масштабируемый отдельный i:
distance(i) = sum_m(x(m,i+1) - x(m,i-1)).
Алгоритм сортирует каждую размерность отдельно, таким образом, термин neighbors означает соседей в каждой размерности.
У людей того же ранга с более высоким расстоянием есть более высокий шанс выбора (более высокое расстояние лучше).
Можно выбрать различную меру по расстоянию давки, чем функция @distancecrowding по умолчанию. См. Многоцелевые Опции.
Давка расстояния, каждый включает вычисление распространения, которое является частью останавливающегося критерия. Давка расстояния также используется в качестве дополнительного времени в выборе турнира, когда у двух выбранных людей есть тот же ранг.
Распространитесь — распространение является мерой перемещения Множества Парето. Чтобы вычислить распространение, алгоритм gamultiobj сначала оценивает σ, стандартное отклонение толпящейся меры по расстоянию точек, которые находятся на передней стороне Парето с конечным расстоянием. Алгоритм затем оценивает μ, сумму по k индексам целевой функции нормы различия между текущим минимальным значением точка Парето для того индекса и минимальной точкой для того индекса в предыдущей итерации. Распространение затем
spread = (μ + σ) / (μ + k*σ).
Распространение является маленьким, когда экстремальные значения целевой функции не изменяются очень между итерациями (то есть, μ является маленьким), и когда точки на передней стороне Парето распространены равномерно (то есть, σ является маленьким).
gamultiobj использует распространение в останавливающемся условии. Итерации останавливаются, когда распространение не изменяется очень, и финал распространился, меньше, чем в среднем недавние распространения. Смотрите Останавливающиеся Условия.
Первый шаг в алгоритме gamultiobj создает начальную генеральную совокупность. Алгоритм создает генеральную совокупность, или можно дать начальную генеральную совокупность или частичную начальную генеральную совокупность при помощи опции InitialPopulationMatrix (см. Опции Генеральной совокупности). Номер людей в генеральной совокупности определяется к значению опции PopulationSize. По умолчанию gamultiobj создает генеральную совокупность, которая выполнима относительно границ и линейных ограничений, но не обязательно выполнима относительно нелинейных ограничений. Алгоритмом создания по умолчанию является @gacreationuniform, когда нет никаких ограничений или только связанных ограничений и @gacreationlinearfeasible, когда существуют линейные или нелинейные ограничения.
gamultiobj выполняет целевую функцию и ограничения для генеральной совокупности, и использует те значения, чтобы создать музыку к генеральной совокупности.
Основная итерация алгоритма gamultiobj продолжает можно следующим образом.
Выберите родительские элементы для следующего поколения с помощью функции выбора на текущей генеральной совокупности. Единственная встроенная функция выбора, доступная для gamultiobj, является бинарным турниром. Можно также использовать пользовательскую функцию выбора.
Создайте дочерние элементы из выбранных родительских элементов мутацией и перекрестным соединением.
Выиграйте дочерние элементы путем вычисления их значений целевой функции и выполнимости.
Объедините текущую генеральную совокупность и дочерние элементы в одну матрицу, расширенную генеральную совокупность.
Вычислите ранг и толпящееся расстояние для всех людей в расширенной генеральной совокупности.
Обрежьте расширенную генеральную совокупность, чтобы иметь людей PopulationSize путем сохранения соответствующего количества людей каждого ранга.
Следующие условия остановки применяются. Каждое условие остановки сопоставлено с выходным флагом.
| Значение exitflag | Остановка условия |
|---|---|
| 1 | Среднее геометрическое относительного изменения в значении распространения по поколениям |
| 0 | Максимальное количество поколений превышено |
| -1 | Оптимизация отключена выходной функцией или функцией построения графика |
| -2 | Никакая допустимая точка не найдена |
| -5 | Ограничение по времени превышено |
Поскольку выход отмечает 1, среднее геометрическое относительного изменения в распространении имеет множитель ½k для относительного изменения в k th предыдущее поколение.
[1] Цензор, Y. “Оптимальность Парето в Многоцелевых проблемах”, Прикладная Математика. Optimiz., Издание 4, стр 41–59, 1977.
[2] Da Cunha, N. O. и Э. Полак. “Ограниченная Минимизация Под Критериями с векторным знаком на Конечномерных Пробелах”, J. Математика. Анальный. Прикладной, Издание 19, стр 103–124, 1967.
[3] Деб, Kalyanmoy. “Многоцелевая Оптимизация с помощью Эволюционных Алгоритмов”, John Wiley & Sons, Ltd, Чичестер, Англия, 2001.
[4] Zadeh, L. A. “Оптимальность и Критерии Производительности с нескалярным знаком”, Автомат Сделки IEEE. Противоречие, издание AC-8, p. 1, 1963.