Совершенствуйте стартовые точки

О совершенствовании стартовых точек

Если некоторые компоненты вашей проблемы неограничены, GlobalSearch и MultiStart используют искусственные границы, чтобы сгенерировать случайные стартовые точки однородно в каждом компоненте. Однако, если ваша проблема имеет обширные минимумы, вам нужны широко рассеянные стартовые точки, чтобы найти эти минимумы.

Используйте эти методы, чтобы получить широко рассеянные стартовые точки:

Дайте широко разделенные границы в своей структуре problem.
Используйте объект RandomStartPointSet с алгоритмом MultiStart. Установите большое значение свойства ArtificialBound в объекте RandomStartPointSet.
Используйте объект CustomStartPointSet с алгоритмом MultiStart. Использование широко рассеяло стартовые точки.

Существуют преимущества и недостатки каждого метода.

Метод	Преимущества	Недостатки
Дайте границы в `problem`	Автоматическая генерация точки	Делает более комплексный Гессиан
	Может использовать с `GlobalSearch`	Неясный, как большой, чтобы установить границы
	Легкий сделать	Изменения `problem`
	Границы могут быть асимметричными	Только универсальные точки
Большой `ArtificialBound` в `RandomStartPointSet`	Автоматическая генерация точки	`MultiStart` только
	Не изменяет `problem`	Только симметричные, универсальные точки
	Легкий сделать	Неясный, как большой, чтобы установить `ArtificialBound`
`CustomStartPointSet`	Настраиваемый	`MultiStart` только
`CustomStartPointSet`	Не изменяет `problem`	Требует программирования для генерации точек

Методы генерации стартовых точек

Регулярная координатная сетка
Встревоженная сетка
Широко рассеянные точки для неограниченных компонентов

Регулярная координатная сетка

Сгенерировать регулярную координатную сетку стартовых точек:

Сгенерируйте многомерные массивы с ndgrid. Дайте нижнюю границу, интервал и верхнюю границу для каждого компонента.
Например, чтобы сгенерировать набор 3D массивов с
- Первый компонент от –2 до 0, располагая с интервалами 0.5
- Второй компонент от 0 до 2, располагая с интервалами 0.25
- Третий компонент от –10 до 5, располагая с интервалами 1
```
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
```
Поместите массивы в одну матрицу с каждой строкой, представляющей одну стартовую точку. Например:
```
W = [X(:),Y(:),Z(:)];
```
В этом примере W 720 3 матрица.
Поместите матрицу в объект CustomStartPointSet. Например:
```
custpts = CustomStartPointSet(W);
```

Вызовите run с объектом CustomStartPointSet как третий вход. Например,

% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);

Встревоженная сетка

Целочисленные стартовые точки могут привести к меньшему количеству надежных решений, чем немного встревоженные стартовые точки.

Получить встревоженный набор стартовых точек:

Сгенерируйте матрицу стартовых точек как на шагах 1-2 Регулярной координатной сетки.
Встревожьте стартовые точки путем добавления случайной нормальной матрицы с 0 средними и относительно небольшими отклонениями.
Для примера в Регулярной координатной сетке, после создания матрицы W, добавляет возмущение:
```
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
W = [X(:),Y(:),Z(:)];
W = W + 0.01*randn(size(W));
```
Поместите матрицу в объект CustomStartPointSet. Например:
```
custpts = CustomStartPointSet(W);
```

Вызовите run с объектом CustomStartPointSet как третий вход. Например,

% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);

Широко рассеянные точки для неограниченных компонентов

Некоторые компоненты вашей проблемы могут испытать недостаток в верхних или нижних границах. Например:

Несмотря на то, что никакие явные границы не существуют, существуют уровни, которых не могут достигнуть компоненты. Например, если один компонент представляет вес одного ромба, существует неявная верхняя граница 1 кг (Ромб Надежды находится под 10 г). В таком случае дайте неявное, связанное как верхнюю границу.
Действительно нет никакой верхней границы. Например, размер компьютерного файла в байтах не имеет никакой эффективной верхней границы. Самый большой размер может быть в гигабайтах или терабайтах сегодня, но через 10 лет, кто знает?

Для действительно неограниченных компонентов можно использовать следующие методы выборки. Сгенерировать приблизительно 1/n точки в каждой области (exp (n), exp (n +1)), используют следующую формулу. Если u случаен и равномерно распределен от 0 до 1, то r = 2u – 1 равномерно распределен между –1 и 1. Взять

$y = sgn (r) (\exp (1 / | r |) - e) .$

y симметричен и случаен. Для переменной, ограниченной ниже lb, взять

$y = lb + (\exp (1 / u) - e) .$

Точно так же для переменной, ограниченной выше ub, взять

$y = ub - (\exp (1 / u) - e) .$

Например, предположите, что у вас есть 3D проблема с

x (1)> 0
x (2) <100
x (3) неограниченный

Сделать 150 стартовых точек, удовлетворяющих эти ограничения:

u = rand(150,3);
r1 = 1./u(:,1);
r1 = exp(r1) - exp(1);
r2 = 1./u(:,2);
r2 = -exp(r2) + exp(1) + 100;
r3 = 1./(2*u(:,3)-1);
r3 = sign(r3).*(exp(abs(r3)) - exp(1));
custpts = CustomStartPointSet([r1,r2,r3]);

Следующее является вариантом этого алгоритма. Сгенерируйте номер между 0 и бесконечность методом для нижних границ. Используйте этот номер в качестве радиуса точки. Сгенерируйте другие компоненты точки путем взятия случайных чисел для каждого компонента и умножьтесь радиусом. Можно нормировать случайные числа, прежде, чем умножиться радиусом, таким образом, их норма равняется 1. Для обработанного примера этого метода смотрите MultiStart Без Границ, Широко Рассеянных Стартовых точек.

Пример: поиск лучшего решения

MultiStart не удается найти глобальный минимум в Нескольких Локальных Минимумах Через MultiStart. Существует два простых способа искать лучшее решение:

Используйте больше стартовых точек
Дайте более трудные границы на пространстве поиска

Настройте объект MultiStart и структура задачи:

problem = createOptimProblem('fminunc',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fminunc,'Algorithm','quasi-newton'));
ms = MultiStart;

Используйте больше стартовых точек

Запустите MultiStart на проблеме для 200 стартовых точек вместо 50:

rng(14,'twister') % for reproducibility
[x,fval,eflag,output,manymins] = run(ms,problem,200)

MultiStart completed some of the runs from the start points.

53 out of 200 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-06 *

   -0.2284   -0.5567


fval =

   2.1382e-12


eflag =

     2


output = 

  struct with fields:

                funcCount: 32670
         localSolverTotal: 200
       localSolverSuccess: 53
    localSolverIncomplete: 147
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵53 out of 200 local solver runs converged with a positive local solver exit flag.'

manymins = 
  1x53 GlobalOptimSolution

  Properties:
    X
    Fval
    Exitflag
    Output
    X0

На этот раз MultiStart нашел глобальный минимум и нашел 51 локальный минимум.

Чтобы видеть область значений локальных решений, введите histogram([manymins.Fval],10).

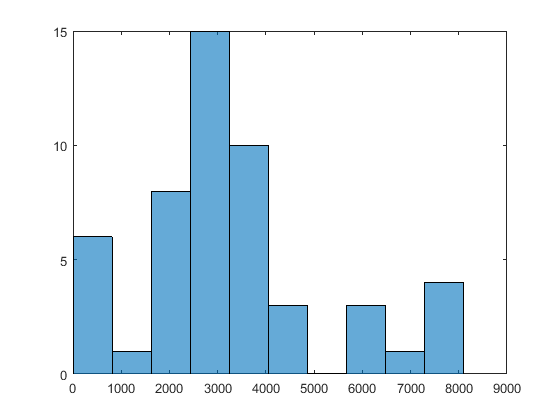
Более трудный привязанный стартовые точки

Предположим, что вы полагаете, что интересные локальные решения имеют абсолютные значения всех компонентов меньше чем 100. Значение по умолчанию привязанного стартовые точки 1000. Чтобы использовать различное значение связанного, сгенерируйте RandomStartPointSet с набором свойств ArtificialBound к 100:

startpts = RandomStartPointSet('ArtificialBound',100,...
    'NumStartPoints',50);
[x,fval,eflag,output,manymins] = run(ms,problem,startpts)

MultiStart completed some of the runs from the start points.

29 out of 50 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-08 *

    0.9725   -0.6198


fval =

   1.4955e-15


eflag =

     2


output = 

  struct with fields:

                funcCount: 7431
         localSolverTotal: 50
       localSolverSuccess: 29
    localSolverIncomplete: 21
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵29 out of 50 local solver runs converged with a positive local solver exit flag.'

manymins = 
  1x25 GlobalOptimSolution

  Properties:
    X
    Fval
    Exitflag
    Output
    X0

MultiStart нашел глобальный минимум и нашел 22 отличных локальных решения. Чтобы видеть область значений локальных решений, введите histogram([manymins.Fval],10).

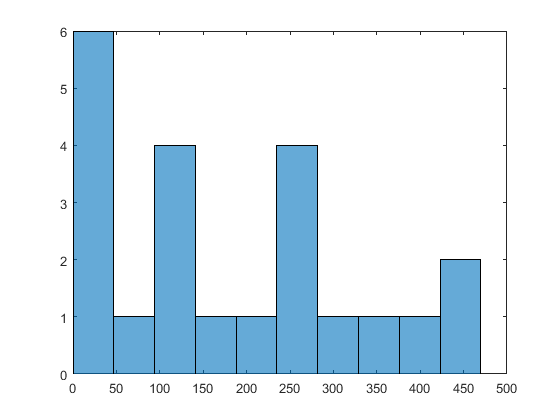
По сравнению с минимумами, найденными в Использовании Больше Стартовых точек, это выполнение, найденное лучше (меньшие) минимумы, и, имел более высокий процент успешных выполнений.

Документация