surrogateoptsurrogateoptСуррогатный алгоритм оптимизации чередуется между двумя фазами.
Создайте Суррогат — Создают случайные точки options.MinSurrogatePoints в границах. Выполните (дорогую) целевую функцию в этих точках. Создайте суррогат целевой функции путем интерполяции радиальной основной функции через эти точки.
Поиск Минимума — Поиск минимума целевой функции путем выборки нескольких тысяч случайных точек в границах. Оцените оценочную функцию на основе суррогатного значения в этих точках и на расстояниях между ними и точками, где (дорогая) целевая функция была выполнена. Выберите лучшую точку в качестве кандидата, как измерено оценочной функцией. Выполните целевую функцию в лучшей точке кандидата. Эта точка называется adaptive point. Обновите суррогат с помощью этого значения и ищите снова.
Во время фазы Construct Surrogate алгоритм создает точки выборки из квазислучайной последовательности. Построение интерполирующей радиальной основной функции берет, по крайней мере, nvars + 1 точка выборки, где nvars является количеством проблемных переменных. Значением по умолчанию options.MinSurrogatePoints является 2*nvars или 20, какой бы ни больше.
Алгоритм останавливает Поиск фазы Minimum, когда все поисковые точки слишком близки (меньше, чем опция MinSampleDistance) к точкам, где целевая функция была ранее выполнена. Смотрите Поиск Минимальных Деталей. Этот переключатель от Поиска фазы Minimum называется surrogate reset.
Суррогатное описание алгоритма оптимизации использует следующие определения.
Текущий — точка, где целевая функция была выполнена последний раз.
Действующий — точка с наименьшим значением целевой функции среди всех оцененных начиная с нового суррогатного сброса.
Лучше всего — точка с наименьшим значением целевой функции среди всех оцененных до сих пор.
Начальная буква — точки, если таковые имеются, что вы передаете решателю в опции InitialPoints.
Случайные точки — Точки в фазе Construct Surrogate, где решатель выполняет целевую функцию. Обычно решатель берет эти точки из квазислучайной последовательности, масштабируемой и переключенной, чтобы остаться в границах. Квазислучайная последовательность подобна псевдослучайной последовательности, такой как rand, возвращается, но более равномерно расположен с интервалами. См. https://en.wikipedia.org/wiki/Low-discrepancy_sequence. Однако, когда количество переменных выше 500, решатель берет точки из латинской последовательности гиперкуба. См. https://en.wikipedia.org/wiki/Latin_hypercube_sampling.
Адаптивные точки — Точки в Поиске фазы Minimum, где решатель выполняет целевую функцию.
Оценочная функция — Видит Определение Оценочной функции.
Оцененные точки — Все точки, в которых известно значение целевой функции. Эти точки включают начальные точки, точки Суррогата Построения и Поиск Минимальных точек, в которых решатель выполняет целевую функцию.
'SamplePoints' . Псевдослучайные точки, где решатель оценивает оценочную функцию во время Поиска фазы Minimum. Эти точки не являются точками, в которых решатель выполняет целевую функцию, за исключением описанного в поисках Минимальных Деталей.
Чтобы создать суррогат, алгоритм выбирает квазислучайные точки в границах. Если вы передаете начальный набор точек в опции InitialPoints, алгоритм использует те точки и новые квазислучайные точки (при необходимости), чтобы достигнуть в общей сложности options.MinSurrogatePoints. На последующих фазах Construct Surrogate алгоритм использует квазислучайные точки options.MinSurrogatePoints. Алгоритм выполняет целевую функцию в этих точках.
Алгоритм создает суррогат как интерполяцию целевой функции при помощи интерполятора радиальной основной функции (RBF). Интерполяция RBF имеет несколько удобных свойств, которые делают ее подходящей для построения суррогата:
Интерполятор RBF задан с помощью той же формулы в любом количестве размерностей и с любым числом точек.
Интерполятор RBF берет заданные значения в оцененных точках.
Оценка интерполятора RBF занимает время.
Добавление точки к существующей интерполяции занимает относительно мало времени.
Построение интерполятора RBF включает решение N на n линейной системы уравнений, где N является количеством суррогатных точек. Когда Пауэлл [1] показал, эта система имеет уникальное решение для многих RBFs.
surrogateopt использует кубический RBF с линейным хвостом. Этот RBF минимизирует меру тряски. Смотрите Гутманна [4].
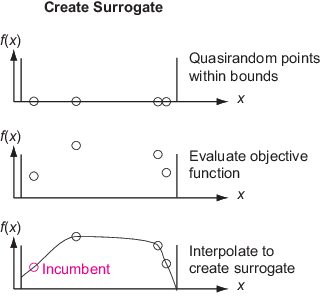
Алгоритм использует только начальные точки и случайные точки в первой фазе Construct Surrogate, и использует только случайные точки в последующих фазах Construct Surrogate. В частности, алгоритм не использует адаптивных точек от Поиска фазы Minimum в этом суррогате.
Решатель ищет минимум целевой функции путем выполнения процедуры, которая связана с локальным поиском. Решатель инициализирует scale для поиска со значением 0.2. Шкала похожа на поисковый радиус области или размер mesh в поиске шаблона. Решатель начинает с действующей точки, которая является точкой с наименьшим значением целевой функции начиная с последнего суррогатного сброса. Решатель ищет минимум merit function, который относится и к суррогату и к расстоянию от существующих поисковых точек, чтобы попытаться сбалансировать минимизацию суррогата и поиск пробела. См. Определение Оценочной функции.
Решатель добавляет сотни или тысячи псевдослучайных векторов с масштабированной длиной к действующей точке, чтобы получить sample points. Эти векторы имеют нормальные распределения, переключенные и масштабированные границами в каждой размерности и умноженные на шкалу. При необходимости решатель изменяет точки выборки так, чтобы они остались в границах. Решатель оценивает оценочную функцию при точках выборки, но не в любой точке в options.MinSampleDistance ранее оцененной точки. Точка с самым низким значением оценочной функции называется адаптивной точкой. Решатель оценивает значение целевой функции в адаптивной точке и обновляет суррогат с этим значением. Если значение целевой функции в адаптивной точке достаточно ниже, чем действующее значение, то решатель считает поиск успешным и устанавливает адаптивную точку как должностное лицо. В противном случае решатель считает поиск неудачным и не изменяет должностное лицо.
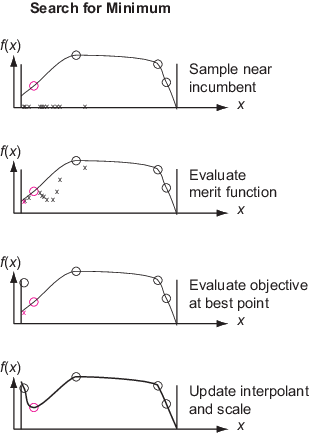
Решатель изменяет шкалу, когда первое из этих условий соблюдают:
Три успешных поисковых запросов происходят начиная с последнего изменения шкалы. В этом случае шкала удвоена до максимальной длины шкалы времен 0.8 размер поля, заданного границами.
Неудачные поисковые запросы max(5,nvar) происходят начиная с последнего изменения шкалы, где nvar является количеством проблемных переменных. В этом случае шкала разделена на два, вниз к минимальной длине шкалы времен 1e-5 размер поля, заданного границами.
Таким образом случайный поиск в конечном счете концентрируется около действующей точки, которая имеет маленькое значение целевой функции. Затем решатель геометрически уменьшает шкалу к минимальной длине шкалы.
Решатель не оценивает оценочную функцию при точках в options.MinSampleDistance оцененной точки (см. Определения для Суррогатной Оптимизации). Переключатели решателя от Поиска фазы Minimum к фазе Construct Surrogate (другими словами, выполняет суррогатный сброс), когда все точки выборки в MinSampleDistance оцененных точек. Обычно этот сброс происходит после того, как решатель уменьшает шкалу так, чтобы все точки выборки плотно кластеризировались вокруг должностного лица.
Оценочная функция заслуга f (x) является взвешенной комбинацией двух условий:
Масштабированный суррогат. Задайте min s как минимальное суррогатное значение среди точек выборки, s макс. как максимум и s (x) как суррогатное значение в точке x. Затем масштабированный суррогатный S (x)
s (x) является неотрицательным и является нулем в точках x, которые имеют минимальное суррогатное значение среди точек выборки.
Масштабированное расстояние. Задайте xj, j = 1, …, k, когда k оценил точки. Defiine dij как расстояние от точки выборки i к оцененной точке k. Установите min d = min (dij) и d макс. = макс. (dij), где минимум и максимум взяты по всему i и j. Масштабированное расстояние D (x)
где d (x) является минимальным расстоянием точки x к оцененной точке. D (x) является неотрицательным и является нулем в точках x, которые максимально далеки от оцененных точек. Так, минимизация D (x) приводит алгоритм к точкам, которые далеки от оцененных точек.
Оценочная функция является выпуклой комбинацией масштабированного суррогата и масштабируемого расстояния. Для веса w с 0 <w <1, оценочная функция
Большое значение w дает важность для суррогатных значений, заставляя поиск минимизировать суррогат. Маленькое значение w дает важность для точек, которые далеки от оцененных точек, ведя поиск в новые области. Во время Поиска фазы Minimum, вес циклы w через эти четыре значения, как предложил Режис и Сапожник [2]: 0.3, 0.5, 0.7, и 0.95.
surrogateoptПараллельный алгоритм surrogateopt отличается от последовательного алгоритма можно следующим образом:
Параллельный алгоритм поддерживает очередь точек, на которых можно выполнить целевую функцию. Эта очередь является на 30% более многочисленной, чем количество параллельных рабочих, окруженных. Очередь является более многочисленной, чем количество рабочих, чтобы свести к минимуму вероятность, что рабочий неактивен, потому что никакой смысл не доступен, чтобы оценить.
Планировщик берет точки из очереди способом FIFO и присваивает их рабочим, когда они становятся неактивными, асинхронно.
Когда переключатели алгоритма между фазами (Поиск Суррогата Минимума и Построения), существующие оцениваемые точки остаются в обслуживании, и любые другие точки в очереди сбрасываются (отброшенный от очереди). Так, обычно, количество случайных точек, которые алгоритм создает для фазы Construct Surrogate, в большей части options.MinSurrogatePoints + PoolSize, где PoolSize является количеством параллельных рабочих. Точно так же после суррогатного сброса, алгоритм все еще имеет PoolSize - 1 адаптивные точки, что его рабочие оценивают.
В настоящее время найдите что-либо подобное суррогатной оптимизации, не обязательно дает восстанавливаемые результаты, из-за невоспроизводимости параллельной синхронизации, которая может привести к различным путям к выполнению.
[1] Пауэлл, M. J. D. Теория Радиального Приближения Основной функции в 1 990. В Свете, W. A. (редактор), Усовершенствования в Числовом Анализе, Объем 2: Вейвлеты, Алгоритмы Подразделения и Радиальные Основные функции. Нажатие Clarendon, 1992, стр 105–210.
[2] Режис, R. G. и К. А. Шоемэкер. Стохастический Радиальный Метод Основной функции для Глобальной Оптимизации Дорогих Функций. INFORMS J. Вычисляя 19, 2007, стр 497–509.
[3] Ван, Y. и К. А. Шоемэкер. Общая Стохастическая Среда Алгоритма для Минимизации Дорогих Целевых функций Черного квадрата На основе Суррогатных Моделей и Анализа чувствительности. arXiv:1410.6271v1 (2014). Доступный по https://arxiv.org/pdf/1410.6271.
[4] Гутманн, H.-M. Радиальный Метод Основной функции для Глобальной Оптимизации. Журнал Глобальной Оптимизации 19, март 2001, стр 201–227.