Непрерывно-дискретные методы преобразования

Выбор метода преобразования

Команда c2d дискретизирует непрерывно-разовые модели. С другой стороны d2c преобразовывает модели дискретного времени в непрерывное время. И команды поддерживают несколько дискретизаций и методов интерполяции, как показано в следующей таблице.

Метод дискретизации	Используйте когда
Нулевой порядок содержит	Вы хотите точную дискретизацию во временном интервале для входных параметров лестницы.
Хранение первого порядка	Вы хотите точную дискретизацию во временном интервале для кусочных линейных входных параметров.
Отображение импульсного инварианта (только `c2d`)	Вы хотите точную дискретизацию во временном интервале для импульсных входных параметров train.
Приближение Тастина	Вы хотите хорошее соответствие в частотном диапазоне между непрерывным - и моделями дискретного времени. Ваша модель имеет важную динамику на некоторой особой частоте.
Нулевое полюсное соответствие с эквивалентами	У вас есть модель SISO. Вы хотите хорошее соответствие в частотном диапазоне между непрерывным - и моделями дискретного времени.
Наименьшие квадраты (Control System Toolbox) (только `c2d`)	У вас есть модель SISO. Вы хотите хорошее соответствие в частотном диапазоне между непрерывным - и моделями дискретного времени. Вы хотите получить быструю системную динамику, но должны использовать больший шаг расчета.

Нулевой порядок содержит

Метод Хранения Нулевого Порядка (ZOH) обеспечивает точное совпадение между непрерывным - и системами дискретного времени во временном интервале для входных параметров лестницы.

Следующая блок-схема иллюстрирует, что дискретизация "нулевой порядок содержит_{" Hd} (z) непрерывно-разовой линейной модели H (s).

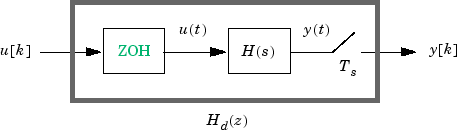
Блок ZOH генерирует непрерывно-разовый входной сигнал u (t) путем содержания каждого демонстрационного значения u (k), постоянный за один демонстрационный период:

$u (t) = u [k], k T_{s} \leq t \leq (k + 1) T_{s}$

u сигнала (t) является входом к непрерывной системе H (s). Вывод y [k] результаты выборки y (t) каждый _Ts секунды.

С другой стороны, учитывая дискретную систему _Hd (z), d2c создает непрерывную систему H (s). Дискретизация ZOH H (s) совпадает с _Hd (z).

Дискретное-к-непрерывному преобразование ZOH имеет следующие ограничения:

d2c не может преобразовать модели LTI с полюсами в z = 0.
Для моделей LTI дискретного времени, имеющих отрицательные действительные полюса, ZOH, преобразование d2c создает непрерывную систему с высшим порядком. Порядок модели увеличивается, потому что отрицательный действительный полюс в области z сопоставляет с чистым мнимым значением в области s. Такое отображение приводит к непрерывно-разовой модели с комплексными данными. Чтобы избежать этой проблемы, программное обеспечение вместо этого вводит сопряженную пару комплексных полюсов в области s.

Метод ZOH для систем с задержками

Можно использовать метод ZOH, чтобы дискретизировать SISO или MIMO непрерывно-разовые модели с задержками. Метод ZOH приводит к точной дискретизации для систем с входными задержками, выходными задержками или транспортными задержками.

Для систем с внутренними задержками (задерживается в обратной связи), результаты метода ZOH в аппроксимированных дискретизациях. Следующая фигура иллюстрирует систему с внутренней задержкой.

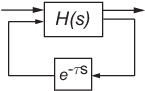
Для таких систем c2d выполняет следующие действия, чтобы вычислить аппроксимированную дискретизацию ZOH:

Анализирует задержку τ как $τ = k T_{s} + ρ$ с $0 \leq ρ < T_{s}$ .
Поглощает дробную задержку $ρ$ в H (s).
Дискретизирует H (s) к H (z).
Представляет целочисленный фрагмент задержки _kTs как внутренняя задержка дискретного времени z ^–k. Финал дискретизированная модель появляется в следующей фигуре:

Хранение первого порядка

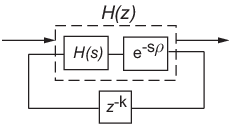
Метод Хранения первого порядка (FOH) обеспечивает точное совпадение между непрерывным - и системами дискретного времени во временном интервале для кусочных линейных входных параметров.

FOH отличается от ZOH базовым механизмом хранения. Чтобы повернуть входные выборки u [k] в непрерывный вход u (t), FOH использует линейную интерполяцию между выборками:

$u (t) = u [k] + \frac{t - k T_{s}}{T_{s}} (u [k + 1] - u [k]), k T_{s} \leq t \leq (k + 1) T_{s}$

В целом этот метод более точен, чем ZOH для систем, управляемых сглаженными входными параметрами.

Этот метод FOH отличается от стандартного причинного FOH и более соответственно called triangle approximation (см. [2], p. 228). Метод также известен как инвариантное пандусом приближение.

Метод FOH для систем с задержками

Можно использовать метод FOH, чтобы дискретизировать SISO или MIMO непрерывно-разовые модели с задержками. Метод FOH обрабатывает задержки таким же образом как метод ZOH. См. Метод ZOH для Систем с Задержками.

Инвариантное импульсом отображение

Инвариантное импульсом отображение производит модель дискретного времени с тем же импульсным ответом как непрерывная система времени. Например, сравните импульсный ответ непрерывной системы первого порядка с инвариантной импульсом дискретизацией:

G = tf(1,[1,1]);
Gd1 = c2d(G,0.01,'impulse');
impulse(G,Gd1)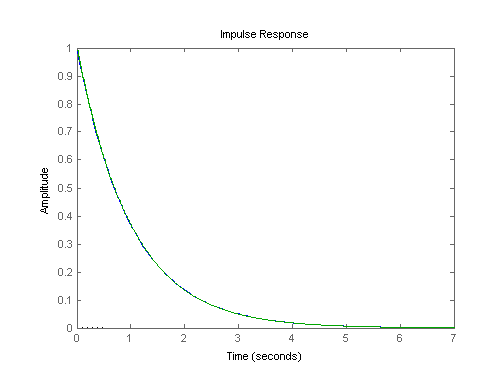

Импульсный график ответа показывает, что импульсные ответы непрерывных и дискретизированных систем соответствуют.

Инвариантное импульсом отображение для систем с задержками

Можно использовать отображение импульсного инварианта, чтобы дискретизировать SISO или MIMO непрерывно-разовые модели с задержками, за исключением того, что метод не поддерживает модели ss с внутренними задержками. Для поддерживаемых моделей инвариантное импульсом отображение приводит к точной дискретизации задержки.

Приближение Тастина

Тастин или билинейное приближение приводят к лучшему соответствию частотного диапазона между непрерывно-разовыми и дискретизированными системами. Этот метод связывает s - область и z - доменные передаточные функции с помощью приближения:

$z = e^{s T_{s}} \approx \frac{1 + s T_{s} / 2}{1 - s T_{s} / 2} .$

В преобразованиях c2d дискретизация _Hd (z) непрерывной передаточной функции H (s):

$H_{d} (z) = H (s^{'}), s^{'} = \frac{2}{T_{s}} \frac{z - 1}{z + 1}$

Точно так же преобразование d2c полагается на обратное соответствие

$H (s) = H_{d} (z^{'}), z^{'} = \frac{1 + s T_{s} / 2}{1 - s T_{s} / 2}$

Когда вы преобразовываете модель в пространстве состояний с помощью метода Тастина, состояния не сохраняются. Преобразование состояния зависит от матриц пространства состояний и имеет ли система задержки. Например, для явного (E = I) непрерывно-разовая модель без задержек, вектор состояния w [k] дискретизированной модели связан с непрерывно-разовым вектором состояния x (t):

$w [k T_{s}] = (I - A \frac{T_{s}}{2}) x (k T_{s}) - \frac{T_{s}}{2} B u (k T_{s}) = x (k T_{s}) - \frac{T_{s}}{2} (A x (k T_{s}) + B u (k T_{s})) .$

_Ts является шагом расчета модели дискретного времени. A и B являются матрицами пространства состояний непрерывно-разовой модели.

Приближение Тастина с предварительным деформированием частоты

Если ваша система имеет важную динамику на особой частоте, которую вы хотите, чтобы преобразование сохранило, можно использовать метод Тастина с предварительным деформированием частоты. Этот метод гарантирует соответствие между непрерывным - и ответами дискретного времени на частоте перед деформацией.

Приближение Тастина с предварительным деформированием частоты использует следующее преобразование переменных:

$H_{d} (z) = H (s^{'}), s^{'} = \frac{ω}{загар (ω T_{s} / 2)} \frac{z - 1}{z + 1}$

Эта замена переменной гарантирует соответствие непрерывного - и частотные характеристики дискретного времени на частоте перед деформацией ω из-за следующего соответствия:

$H (j ω) = H_{d} (e^{j ω T_{s}})$

Приближение Тастина для систем с задержками

Можно использовать приближение Тастина, чтобы дискретизировать SISO или MIMO непрерывно-разовые модели с задержками.

По умолчанию метод Тастина округляет любую задержку к самому близкому кратному шаг расчета. Поэтому для любого tau с временной задержкой, целочисленный фрагмент задержки, k*Ts, сопоставляет с задержкой периодов выборки k в дискретизированной модели. Этот подход игнорирует остаточную дробную задержку, tau - k*Ts.

Вы можете, чтобы аппроксимировать дробный фрагмент задержки дискретным фильтром все-передачи (фильтр Thiran) заданного порядка. Для этого используйте опцию FractDelayApproxOrder c2dOptions.

Чтобы понять, как метод Тастина обрабатывает системы с задержками, считайте следующую модель в пространстве состояний SISO G (s). Модель ввела, задерживают _τi, выводят, задерживают _τo и внутреннюю задержку τ.

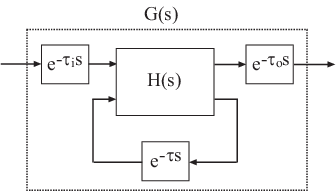
Следующие данные показывают общий результат дискретизации G (s) с помощью метода Тастина.

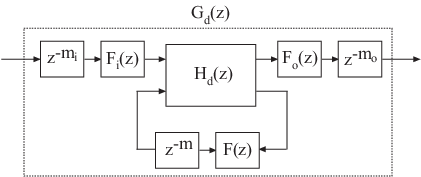
По умолчанию c2d преобразовывает задержки в чистые целочисленные задержки. Команда c2d вычисляет целочисленные задержки путем округления каждой задержки к самому близкому кратному шаг расчета _Ts. Таким образом, в случае по умолчанию, _mi = вокруг (_τi/_Ts), _mo = round (_τo/_Ts), и m = round (τ/_Ts).. Также в этом случае, _Fi (z) = _Fo (z) = F (z) = 1.

Если вы устанавливаете FractDelayApproxOrder на ненулевое значение, c2d аппроксимирует дробный фрагмент задержек фильтрами Thiran _Fi (z), _Fo (z) и F (z).

Фильтры Thiran добавляют дополнительные состояния в модель. Максимальным количеством дополнительных состояний для каждой задержки является FractDelayApproxOrder.

Например, для входа задерживают _τi, порядок фильтра Thiran_{, который Fi} (z):

order (_Fi (z)) = max (ceil (_τi/_Ts), FractDelayApproxOrder).

Если ceil (_τi/_Ts) <FractDelayApproxOrder, фильтр Thiran_{, Fi} (z) аппроксимирует целый вход, задерживает _τi. Если ceil (_τi/_Ts)> FractDelayApproxOrder, Thiran фильтруют, только аппроксимирует фрагмент входной задержки. В этом случае c2d представляет остаток от входной задержки как цепочка единичных задержек ^_z–mi, где

_mi = ceil (_τi/_Ts) – FractDelayApproxOrder

c2d использует фильтры Thiran, и FractDelayApproxOrder похожим способом аппроксимировать вывод задерживают _τo и внутреннюю задержку τ.

Когда вы, модели discretizetf и zpk с помощью метода Тастина, c2d сначала агрегировали весь вход, вывод и транспорт, задерживаете в одну транспортную задержку _ИТОГ τ для каждого канала. c2d затем аппроксимирует _ИТОГ τ как фильтр Thiran и цепочку единичных задержек таким же образом, как описано для каждой из задержек моделей ss.

Для получения дополнительной информации о фильтрах Thiran, смотрите страницу с описанием thiran и [4].

Нулевое полюсное соответствие с эквивалентами

Этот метод преобразования, которое вычисляет нулевые полюсные эквиваленты соответствия, применяется только к системам SISO. Непрерывные и дискретизированные системы имеют соответствие с усилениями DC. Их полюса и нули связаны преобразованием:

$z_{i} = e^{s_{i} T_{s}}$

где:

_zi является i th полюс или нуль системы дискретного времени.
_si является i th полюс или нуль непрерывно-разовой системы.
_Ts является шагом расчета.

См. [2] для получения дополнительной информации.

Нулевое полюсное соответствие для систем с задержками

Можно использовать нулевое полюсное соответствие, чтобы дискретизировать непрерывно-разовые модели SISO с задержкой, за исключением того, что метод не поддерживает модели ss с внутренними задержками. Нулевой полюсный метод сопоставления обрабатывает задержки таким же образом как приближение Тастина. Смотрите Приближение Тастина для Систем с Задержками.

Наименьшие квадраты

Метод наименьших квадратов минимизирует ошибку между частотными характеристиками систем непрерывно-разового и дискретного времени до частоты Найквиста с помощью векторно подходящего подхода оптимизации. Этот метод полезен когда это необходимо, чтобы получить быструю системную динамику, но должен использовать больший шаг расчета, например, когда вычислительные ресурсы ограничиваются.

Этот метод поддерживается только функцией c2d и только для систем SISO.

Как с приближением Тастина и нулевым полюсным соответствием, метод наименьших квадратов обеспечивает хорошее соответствие между частотными характеристиками исходной непрерывно-разовой системы и конвертированной системы дискретного времени. Однако при использовании метода наименьших квадратов с:

Тот же шаг расчета как приближение Тастина или нулевое полюсное соответствие, вы получаете меньшее различие между частотными характеристиками непрерывно-разового и дискретного времени.
Более низкий шаг расчета, чем, что вы использовали бы с приближением Тастина или нулевым полюсным соответствием, можно все еще получить результат, который удовлетворяет требования. Выполнение так полезно, если вычислительные ресурсы ограничиваются, поскольку более медленный шаг расчета означает, что процессор должен сделать меньше, работают.

Ссылки

[1] Åström, К.Дж. и Б. Виттенмарк, Управляемые компьютером Системы: Теория и Проект, Prentice Hall, 1990, стр 48-52.

[2] Франклин, G.F., Пауэлл, D.J., и рабочий, М.Л., цифровое управление динамических систем (3-й выпуск), Prentice Hall, 1997.

[3] Смит, J.O. III, "импульсный метод инварианта", физическая обработка звукового сигнала, август 2007. https://www.dsprelated.com/dspbooks/pasp/Impulse_Invariant_Method.html.

[4] Т. Лааксо, В. Вэлимэки, "Разделяя Единичную задержку", Журнал Обработки сигналов IEEE, Издание 13, № 1, p.30-60, 1996.

Документация