Как описано в Изображениях в MATLAB, MATLAB® хранит большинство изображений как двумерные массивы (т.е. матрицы), в котором каждый элемент матрицы соответствует одному пикселю в отображенном изображении. К местоположениям доступа в изображениях Image Processing Toolbox™ использует несколько различных систем координат изображений в качестве соглашений для представления изображений как массивы.
Пиксельные Индексы — поскольку изображения являются массивами, можно использовать стандартную индексацию MATLAB.
Пространственные координаты — можно рассмотреть местоположения в изображениях как позиции по плоскости с помощью Декартовых координат.
Часто, самый удобный метод для выражения местоположений в изображении должен использовать пиксельные индексы. Изображение обработано как сетка дискретных элементов, упорядоченных сверху донизу, и слева направо, как проиллюстрировано следующей фигурой.
Пиксельные индексы
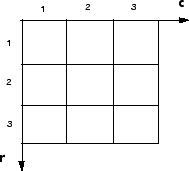
Для пиксельных индексов строка увеличивается вниз, в то время как столбец увеличивается направо. Пиксельные индексы являются целочисленными значениями и диапазоном от 1 до длины строки или столбца.
Существует взаимно-однозначное соответствие между пиксельными индексами и индексами для первых двух матричных размерностей в MATLAB. Например, данные для пикселя в пятой строке, второй столбец хранится в элементе матрицы (5,2). Вы используете нормальную матрицу MATLAB, преобразовывающую в нижний индекс, чтобы получить доступ к значениям отдельных пикселей. Например, код MATLAB
I(2,15)
возвращает значение пикселя в строке 2, столбце 15 изображения I. Точно так же код MATLAB
RGB(2,15,:)
возвращает R, G, значения B пикселя в строке 2, столбце 15 изображения RGB.
Соответствие между пиксельными индексами и индексами для первых двух матричных размерностей в MATLAB делает отношение между матрицей данных изображения и способом, которым изображение отображено легкое понять.
Другой метод для выражения местоположений в изображении должен использовать систему постоянно переменных координат, а не дискретных индексов. Это позволяет вам рассмотреть изображение как покрытие квадратной закрашенной фигуры, например. В системе пространственной координаты как это местоположения в изображении являются позициями по плоскости, и они описаны с точки зрения x и y (не строка и столбец как в пиксельной системе индексации). С этой Декартовой точки зрения, (x, y) местоположение такой как (3.2 5.3) значимо, и отлично от пикселя (5,3).
Image Processing Toolbox задает два типа систем пространственной координаты
Внутренние Координаты — система пространственной координаты, которая соответствует пиксельным индексам
Мировые координаты — система пространственной координаты, которая связывает изображение с некоторым другим координатным пространством
По умолчанию тулбокс использует систему пространственной координаты для изображения, которое соответствует пиксельным индексам изображения. Это называется внутренней системой координат и проиллюстрировано в следующей фигуре. Заметьте, что y увеличивается вниз, потому что эта ориентация сопоставима с путем, которым обычно просматриваются цифровые изображения.
Внутренняя система координат
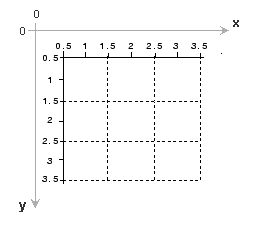
Внутренние координаты (x, y) центральной точки любого пикселя идентичны столбцу и индексам строки для того пикселя. Например, центральная точка пикселя в строке 5, столбец 3 имеет пространственные координаты x = 3.0, y = 5.0. Это соответствие значительно упрощает много функций тулбокса. Следует иметь в виду, однако, что порядок координатной спецификации (3.0 5.0) инвертируется во внутренних координатах относительно пиксельных индексов (5,3).
Несколько функций, в основном, работают с пространственными координатами, а не пиксельными индексами, но, пока вы используете систему пространственной координаты по умолчанию (внутренние координаты), можно задать местоположения с точки зрения их столбцов (x) и строк (y).
При рассмотрении внутренней системы координат обратите внимание, что левый верхний угол изображения расположен в (0.5 0.5), не в (0,0), и правый нижний угол изображения расположен в (numCols + 0.5, numRows + 0.5), где numCols и numRows являются количеством строк и столбцов в изображении. Напротив, верхний левый пиксель является пикселем (1,1), и нижний правый пиксель является пикселем (numRows, numCols). Центр верхнего левого пикселя (1.0, 1.0), и центр нижнего правого пикселя (numCols, numRows). На самом деле центральные координаты каждого пикселя являются оцененным целым числом. Центр пикселя с индексами (r, c) — где r и c являются целыми числами по определению — падает на точку x = c, y = r во внутренней системе координат.
В некоторых ситуациях вы можете хотеть использовать систему мировой координаты (также названный системой пространственной координаты не по умолчанию). Например, вы могли переключить источник путем указывания, что левый верхний угол изображения является точкой (19.0 7.5), а не (0.5 0.5). Или, вы можете хотеть задать систему координат, в которой каждый пиксель покрывает закрашенную фигуру метра 5 на 5 на земле.
Существует несколько способов задать систему мировой координаты: