Географический эллипс от центра, полуглавных осей, эксцентриситета и азимута
[lat,lon] = ellipse1(lat0,lon0,ellipse)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid)
[lat,lon] = ellipse1(___,angleUnit)
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid,angleUnit,npts)
[lat,lon] = ellipse1(trackStr,...)
mat = ellipse1(...)
[lat,lon] = ellipse1(lat0,lon0,ellipse) вычисляет эллипс (эллипсы) с центром (центрами) в lat0,lon0. Эллипс задан третьим входом, который имеет форму [semimajor axis,eccentricity], где вход эксцентриситета может быть двухэлементным вектором - строкой или матрицей 2D столбца. Вход эллипса должен иметь одинаковое число строк как входной скаляр или вектор-столбцы lat0 и lon0. Вход полуглавная ось имеет в градусах длину дуги на сфере. Все замещающие знаки ориентированы так, чтобы их главные оси, запущенные между севером и югом.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset) вычисляет эллипс (эллипсы), где главная ось вращается с должного севера смещением азимута. Угол offset измеряется по часовой стрелке от должного севера. Если offset = [], то никакое смещение не принято.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az) использует вход az, чтобы задать вычисленные дуги эллипса. Азимуты дуги измеряются по часовой стрелке от должного севера. Если az является вектор-столбцом, то длина дуги вычисляется с должного севера. Если az является матрицей 2D столбца, то дуги эллипса вычисляются, начиная в азимуте в первом столбце и заканчиваясь в азимуте во втором столбце. Если az = [], то полный эллипс вычисляется.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid) вычисляет эллипс на эллипсоиде, заданном входом ellipsoid. ellipsoid является referenceSphere, referenceEllipsoid, или объект oblateSpheroid или вектор формы [semimajor_axis eccentricity]. Если не использовано, сфера единичного радиуса, принят. Когда эллипсоид предоставляется, вход, полуглавная ось должна быть в тех же модулях как эллипсоид полуглавные оси. В этой форме вызова, модулях эллипса полуглавная ось не приняты, чтобы быть в градусах.
[lat,lon] = ellipse1(___,angleUnit) где angleUnit задает модули вводов и выводов. angleUnit может быть 'degrees' или 'radians'. Если вы не используете angleUnit, ellipse1 использует 'degrees'.
[lat,lon] = ellipse1(lat0,lon0,ellipse,offset,az,ellipsoid,angleUnit,npts) использует скалярный npts, чтобы определить число точек на вычисленный эллипс. Если npts не использован, 100 точек используются.
[lat,lon] = ellipse1(trackStr,...) где trackStr задает или большой круг ('gc') или локсодрому ('rh') расстояния от центра эллипса.
mat = ellipse1(...) возвращает один выходной аргумент где mat = [lat lon]. Это полезно, если только один эллипс вычисляется.
Можно задать несколько замещающих знаков с общим центром путем обеспечения скалярному lat0 и входным параметрам lon0 и 2D столбцу матрицы ellipse.
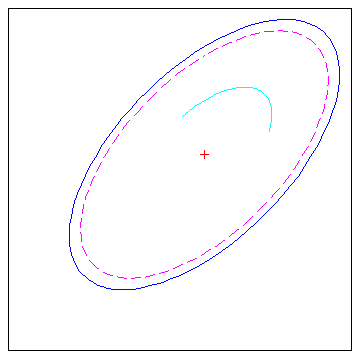
Создайте и постройте маленький эллипс, сосредоточенный в (0º, 0º) с полуглавной осью 10º и полунезначительной осью 5º.
axesm mercator ecc = axes2ecc(10,5); plotm(0,0,'r+') [elat,elon] = ellipse1(0,0,[10 ecc],45); plotm(elat,elon)
Если желаемый радиус известен в некоторой неугловой единице расстояния, используйте радиус, возвращенный функцией earthRadius как вход эллипсоида, чтобы установить модули области значений. (Используйте пустую запись азимута, чтобы задать полный эллипс.)
[elat,elon] = ellipse1(0,0,[550 ecc],45,[],earthRadius('nm'));
plotm(elat,elon,'m--')Для только дуги эллипса введите область значений азимута:
[elat,elon] = ellipse1(0,0,[5 ecc],45,[-30 70]); plotm(elat,elon,'c-')