Этот пример показывает, как создать 2D сетку с помощью meshgrid и ndgrid.
В MATLAB® данные с координатной сеткой означают данные, упорядоченные в сетке. Можно понять упорядоченные данные путем размышления о том, как MATLAB хранит данные в матрицах.
Задайте некоторые данные.
A = gallery('uniformdata',[3 5],0)A = 3×5
0.9501 0.4860 0.4565 0.4447 0.9218
0.2311 0.8913 0.0185 0.6154 0.7382
0.6068 0.7621 0.8214 0.7919 0.1763
MATLAB хранит данные в матрице. Можно думать о A как о наборе мест для элементов, которые упорядочены индексами матрицы. Линейные индексы A:
Любой элемент в матрице может быть получен путем индексации, то есть, путем выяснения элемент в том месте в матрице. ith элемент в A получен A(i).
Получите 7-й элемент в A.
A(7)
ans = 0.4565
Для матрицы m на n можно найти элементы столбца смежными с ith элементом путем возмещения i 1. Чтобы найти элементы строки смежными с ith элементом, сместите i m.
Получите элементы столбца, смежные с A(7).
A(6),A(8)
ans = 0.7621
ans = 0.0185
MATLAB использует подобную идею для создания сеток данных. Сетка не является только набором точек, которые соответствуют определенным геометрическим свойствам. Скорее набор данных с координатной сеткой полагается на упорядоченное отношение среди точек в сетке. Информация о смежности, легко доступная в структуре сетки, очень полезна для многих приложений и особенно основанной на сетке интерполяции.
MATLAB обеспечивает две функции для создания сеток:
meshgrid создает 2D и 3-D сетки, которые являются выровненной Осью декартовой системы координат. Чтобы создать 2D сетку, синтаксисом является [X,Y] = meshgrid(xgv, ygv), где xgv является вектором длины m, и ygv является вектором длины n. meshgrid реплицирует xgv, чтобы сформировать n-by-m матричный X, и это реплицирует ygv, чтобы сформировать другой n-by-m матричный Y. X и Y представляют координаты узлов решетки. Строки X выравниваются с горизонтальным X - ось, и столбцы Y выравниваются с отрицательным Y - ось.
ndgrid создает сетки N-D, которые являются выровненным пробелом массивов. На пробеле массивов оси являются строкой, столбцом, страницей, и т.д. Синтаксисом вызова является [X1, X2, X3,...,Xn] = ndgrid(x1gv, x2gv, x3gv,...,xngv), где x1gv,x2gv,x3gv,...,xngv является векторами, которые охватывают сетку в каждой размерности. X1,X2,X3,...,Xn является выходными массивами, которые могут использоваться для того, чтобы выполнить функции нескольких переменных и для многомерной интерполяции.
Используйте meshgrid, чтобы создать выровненную сетку 2D оси из двух векторов, xgv и ygv.
xgv = [1 2 3]; ygv = [1 2 3 4 5]; [X,Y] = meshgrid(xgv, ygv)
X = 5×3
1 2 3
1 2 3
1 2 3
1 2 3
1 2 3
Y = 5×3
1 1 1
2 2 2
3 3 3
4 4 4
5 5 5
Теперь используйте ndgrid, чтобы создать выровненную сетку 2D пространства от тех же двух векторов, xgv и ygv.
[X1,X2] = ndgrid(xgv,ygv)
X1 = 3×5
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
X2 = 3×5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
Заметьте, что X1 ndgrid является транспонированием X meshgrid. То же самое верно для X2 и Y.
Для данного набора входных параметров meshgrid и функции ndgrid произведут сетки с точно теми же координатами. Единственной разницей между их выходными параметрами является формат координатных массивов. Постройте оба выходных параметров и смотрите, что они - то же самое.
figure() [X1_ndgrid,X2_ndgrid] = ndgrid(1:3,1:5); Z = zeros(3,5); mesh(X1_ndgrid,X2_ndgrid,Z,'EdgeColor','black') axis equal; % Set the axis labeling and title h1 = gca; h1.XTick = [1 2 3]; h1.YTick = [1 2 3 4 5]; xlabel('ndgrid Output')

figure() [X_meshgrid,Y_meshgrid] = meshgrid(1:3, 1:5); mesh(X_meshgrid,Y_meshgrid,Z','EdgeColor','black') axis equal; % Set the axis labeling and title h2 = gca; h2.XTick = [1 2 3]; h2.YTick = [1 2 3 4 5]; xlabel('meshgrid Output')

В зависимости от того, как вы намереваетесь использовать свою сетку, можно предпочесть один формат или другой. Некоторые функции в MATLAB могут потребовать, чтобы ваши данные имели формат meshgrid, в то время как другие могут потребовать формата ndgrid.
Преобразование Между Форматами Сетки. Чтобы преобразовать 2D сетку вывод от meshgrid до формата ndgrid, транспонируйте координатные матрицы:
[X_meshgrid,Y_meshgrid] = meshgrid(1:3, 1:5);
[X1_ndgrid,X2_ndgrid] = ndgrid(1:3,1:5);
isequal(X_meshgrid',X1_ndgrid)
ans =
1
isequal(Y_meshgrid',X2_ndgrid)
ans =
1permute. isequal(permute(X_meshgrid,[2 1]),X1_ndgrid)
ans =
1meshgrid в ndgrid, транспонируйте каждую страницу координатного массива. Для данного массива my_array permute(my_array, [2 1 3]) обменивается строками и столбцами, и результирующий эффект является перемещением каждой страницы:[X_meshgrid,Y_meshgrid,Z_meshgrid] = meshgrid(1:3, 1:5, [1 2]);
[X1_ndgrid,X2_ndgrid,X3_ndgrid] = ndgrid(1:3,1:5, [1 2]);
isequal(permute(X_meshgrid,[2 1 3]),X1_ndgrid)
ans =
1
isequal(permute(Y_meshgrid,[2 1 3]),X2_ndgrid)
ans =
1
isequal(permute(Z_meshgrid,[2 1 3]),X3_ndgrid)
ans =
1Векторы сетки. Входные параметры, которые вы передаете функциям сетки, называются grid vectors. Векторы сетки неявно задают сетку. Рассмотрите два вектора, x1gv = (1:3) и x2gv = (1:5). Можно думать об этих векторах как о наборе координат в направлении x1 и наборе координат в направлении x2, как так:
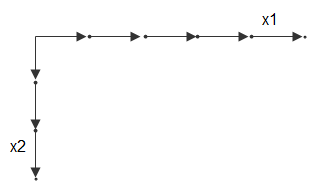
Каждая стрелка показывает на местоположение. Можно использовать эти два вектора, чтобы задать набор узлов решетки, где один набор координат дан x1gv, и другой набор координат дан x2gv. Когда векторы сетки реплицированы, они формируют два координатных массива, которые составляют full grid:
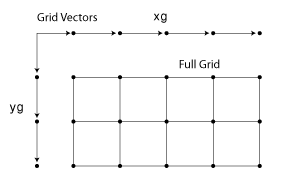
Монотонные и Немонотонные Сетки. Вашими входными векторами сетки может быть monotonic или nonmonotonic. Монотонные векторы содержат значения, что или увеличьтесь в той размерности или уменьшении в той размерности. С другой стороны немонотонные векторы содержат значения, которые колеблются. Если входной вектор сетки является немонотонным, таким как [2 4 6 8 3 1], ndgrid выходные параметры следующее:
[X1,X2] = ndgrid([2 4 6 3 1])
X1 =
2 2 2 2 2
4 4 4 4 4
6 6 6 6 6
3 3 3 3 3
1 1 1 1 1
X2 =
2 4 6 3 1
2 4 6 3 1
2 4 6 3 1
2 4 6 3 1
2 4 6 3 1Регулярные координатные сетки и Нерегулярные координатные сетки. Сетка uniform - та, в которой все соседние точки в данной размерности имеют равный интервал. Например, [X1, X2] = ndgrid([1 3 5 9],[11 13 15]) является универсальной формой с интервалом 2 модулей в каждой размерности.
Не необходимо для интервала в регулярной координатной сетке быть равным во всех размерностях. Например, [X1, X2] = ndgrid([1 2 3 4],[11 13 15]) рассматривается универсальным даже при том, что интервал в X1 и X2 отличается.
Сетка, интервал которой отличается в любой размерности, является сеткой nonuniform. Например, [X1, X2] = ndgrid([1 5 6 9],[11 13 15]) создает нерегулярную координатную сетку, потому что интервал отличается по первому измерению.
|
|
|
| Универсальная форма | Универсальная форма | Неоднородный |
MATLAB позволяет вам представлять сетку в одном из трех представлений: полная сетка, компактная сетка или сетка по умолчанию. Компактная сетка и сетка по умолчанию используются, в основном, для удобства и повышенной эффективности.
Полная сетка. full grid - тот, в котором явным образом заданы точки. Выходные параметры ndgrid и meshgrid задают полную сетку.
Компактная Сетка. Явное определение каждой точки в сетке является дорогим с точки зрения памяти. Представление compact grid является способом обойтись без памяти наверху о полной сетке. Компактное представление сетки хранит только векторы сетки вместо полной сетки. (Для получения информации о том, как класс griddedInterpolant использует компактное представление сетки, смотрите Интерполяцию с griddedInterpolant Классом.)
Сетка по умолчанию. Для многих случаев, когда вы анализируете данные, вы заботитесь и о расстояниях между точками в сетке и об их значении. Например, набор данных может представлять ливень в отдельных моментах в географической области. В этом случае вы заботились бы о значении в каждом узле решетки и расстоянии между точкой и ее соседом. В других случаях вы можете заботиться только о значении для данной точки а не об относительных расстояниях. Например, вы могли работать с входными данными от сканирования MRI, где расстояние между точками абсолютно универсально. В этом случае вы заботились бы о значениях точек, но можно быть уверены в абсолютно регулярной координатной сетке. В этом случае представление default grid полезно. default grid representation хранит значение в узле решетки явным образом и создает координаты узла решетки неявно.
Этот пример показывает, как можно использовать сетку по умолчанию вместо полной сетки, чтобы произвести график.
Создайте сетку и функцию, которую вы хотите построить.
[X,Y] = meshgrid(11:15,11:16); Z = X.^2 + Y.^2;
Используйте полную сетку, которую вы создали с meshgrid при помощи X и Y.
figure
surf(X,Y,Z)
title('Full Grid')
Напротив, сделайте, чтобы MATLAB создал сетку по умолчанию вместо того, чтобы использовать полную сетку.
figure
surf(Z)
title('Default Grid')
Заметьте различие в масштабировании осей. Когда вы строите полную сетку X - и Y - ось имеет области значений 11 - 15 и 10 - 16 соответственно. Когда вы строите сетку по умолчанию X - и Y - ось имеет области значений 1 к m и 1 к n, где Z является m на n.
В некоторых случаях вы, возможно, должны аппроксимировать сетку для своих данных. Аппроксимированная сетка может быть идеализирована стандартной сеткой MATLAB путем выбора соответствующего набора векторов сетки. Например, сетка может иметь точки, которые простираются вдоль кривых линий. Набор данных как эта сила происходит, если ваши данные являются долготой и базирующейся широтой:
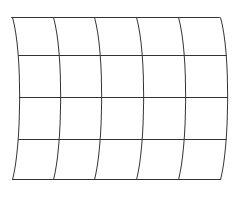
В этом случае, несмотря на то, что входные данные не могут быть с координатной сеткой непосредственно, можно аппроксимировать прямые линии сетки в соответствующих интервалах:
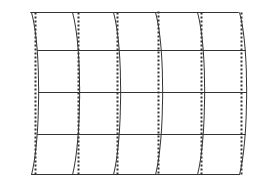
Можно также использовать сетку по умолчанию.
Вырожденная Сетка. degenerate grid является особым случаем сетки, где одно или несколько измерений сетки является одиночными элементами. Одноэлементная размерность может быть внутренней, как в 7:7 в этом примере:
[X1,X2,X3] = ndgrid(1:2:10,7:7,1:3:15);
[X1,X2,X3] = ndgrid(1:2:10,1:3:15,7:7);
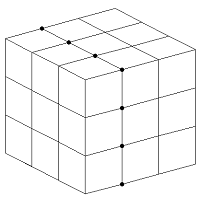
Если вы используете индексацию, чтобы извлечь желаемые данные, результирующая сетка является вырожденной в размерности X3:
[X1,X2,X3] = ndgrid(1:3);
X1_slice = X1(:,:,2)
X1_slice =
1 1 1
2 2 2
3 3 3
X2_slice = X2(:,:,2)
X2_slice =
1 2 3
1 2 3
1 2 3
X3_slice = X3(:,:,2)
X3_slice =
2 2 2
2 2 2
2 2 2Концепция построения сеток очень важна для понимания путей, которыми MATLAB делает основанную на сетке интерполяцию.
В основанной на сетке интерполяции данные, которые будут интерполированы, представлены упорядоченной сеткой. Например, расположение измерений температуры по прямоугольной плоской поверхности в интервалах на 1 см сверху донизу вертикально и слева направо горизонтально рассматривается 2D данными с координатной сеткой. Основанная на сетке интерполяция обеспечивает эффективный способ аппроксимировать температуру в любом местоположении между узлами решетки.
Основанная на сетке интерполяция обеспечивает значительные сбережения в вычислительных издержках, потому что структура с координатной сеткой позволяет MATLAB определять местоположение точки запроса и ее смежных соседей очень быстро. Чтобы понять, как это работает, рассмотрите следующие моменты на 1D сетке:
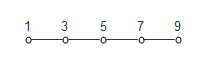
Строки, соединяющие смежные точки, представляют cells сетки. Первая ячейка происходит между x = 1 и x = 3, второе происходит между x = 3 и x = 5 и так далее. Каждый номер представляет координату в сетке. Если бы вы хотите запросить сетку в x = 6, необходимо было бы использовать интерполяцию, потому что 6 явным образом не задан в сетке. Поскольку эта сетка имеет универсальный интервал 2, можно сузить местоположение точки запроса с одним целочисленным делением (6/2 = 3). Это говорит вам, что точка находится в 3-й ячейке сетки. Определение местоположения ячейки в 2D сетке включает выполнение этой операции однажды в каждой размерности. Эта операция называется fast lookup, и MATLAB использует этот метод только, когда данные располагаются в регулярной координатной сетке.
Этот быстрый поиск эффективно определяет местоположение ячейки, содержащей точку запроса Xq. Двоичный поиск продолжает можно следующим образом:
Найдите центральный узел решетки.
Сравните Xq с точкой в центре сетки.
Если Xq является меньше, чем точка, найденная в центре, устраните все узлы решетки, больше, чем центральная точка от поиска. Точно так же, если Xq больше, чем тот, найденный в центре, мы устраняем все узлы решетки, которые являются меньше, чем центральная точка. Обратите внимание на то, что путем выполнения этого, мы уменьшали число точек, которое мы должны искать наполовину.
Найдите центр остающихся узлов решетки и повторения от Шага 2, пока вас не оставят с одним узлом решетки по обе стороны от вашего запроса. Эти две точки отмечают контур ячейки, которая содержит Xq.

Чтобы проиллюстрировать степень двоичных поисков, рассмотрите следующий пример. Перед появлением электронных полномочий кредитной карты единственные продавцы защиты имели против мошеннических покупок по кредитной карте, должен был сравнить номер счета на кредитной карте каждого клиента против списка "плохих" номеров счета. Эти списки были связанными буклетами с десятками тысяч номеров карты, расположенных в порядке возрастания. Сколько сравнений потребовалось бы, чтобы перерывать список 10 000 номеров счета для одной продажи? Оказывается, что для любого списка n, упорядоченного элементы, максимальное количество сравнений будет не больше, чем числом раз, можно разделить пополам список или log2(n). Поэтому поиск кредитной карты возьмет не больше, чем log2(10e3) или приблизительно 13 сравнений. Это - довольно впечатляющее, если бы вы рассматриваете, сколько сравнений потребовалось бы, чтобы выполнить последовательный поиск.
В отличие от этого, рассмотрите проблему с набором данных, имеющий разброс.
x = rand(20,1); y = rand(20,1); scatter(x,y)

Найти точки в непосредственной близости от точки запроса потребовало бы значительно большего количества операций. Если ваши данные могут быть аппроксимированы как сетка, основанная на сетке интерполяция обеспечит существенные сбережения в вычислении и использовании памяти.
Если ваши данные рассеиваются, можно использовать инструменты, детализированные в Интерполяции данных, имеющих разброс.
Методы интерполяции, доступные в MATLAB, создают функции интерполяции, которые передают, хотя выборочные данные указывают. Если бы необходимо было запросить функцию интерполяции при демонстрационном местоположении, вы возвратили бы значение в той точке выборочных данных. В отличие от этого, изогнитесь и появитесь, алгоритмы подбора не обязательно проходят через точки выборочных данных.
Основанная на сетке интерполяция предлагает несколько различных методов для интерполяции. При выборе метода интерполяции имейте в виду, что некоторые требуют большей памяти или более длительное время вычисления, чем другие. Однако вы, возможно, должны обменять эти ресурсы, чтобы достигнуть желаемой гладкости в результате. Следующая таблица предоставляет обзор преимуществ, компромиссов и требований для каждого метода.
| Метод | Описание | Непрерывность | Использование памяти и производительность | Требования |
|---|---|---|---|---|
| NearestNeighbor | Интерполированное значение в точке запроса является значением в самом близком демонстрационном узле решетки. | Прерывистый |
|
|
| Следующий сосед | Интерполированное значение в точке запроса является значением в следующем демонстрационном узле решетки. | Прерывистый | Те же требования к памяти и время вычисления как самый близкий сосед. |
|
| Предыдущий сосед | Интерполированное значение в точке запроса является значением в предыдущем демонстрационном узле решетки. | Прерывистый | Те же требования к памяти и время вычисления как самый близкий сосед. |
|
| Линейный | Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. | C0 |
|
|
| Pchip | Интерполированное значение в точке запроса основано на сохраняющей форму кусочной кубичной интерполяции значений в соседних узлах решетки. | C1 |
|
|
| Кубический | Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. | C1 |
|
|
| Измененный Акима | Интерполированное значение в точке запроса основано на кусочной функции полиномов со степенью самое большее три оцененных использования значений соседних узлов решетки в каждой соответствующей размерности. Формула Акима изменяется, чтобы избежать перерегулирований. | C1 |
|
|
| Сплайн | Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. | C2 |
|
|
У этой фигуры есть некоторые визуальные сравнения различных методов интерполяции для 1D данных.
Сравнение методов интерполяции
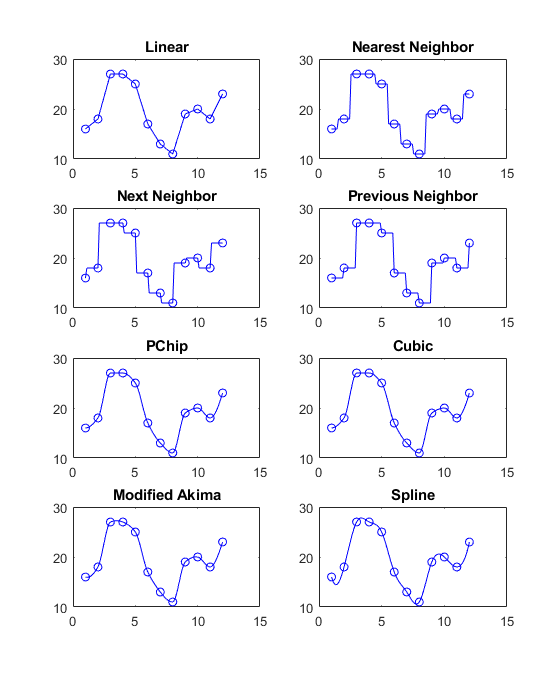
MATLAB оказывает поддержку для основанной на сетке интерполяции несколькими способами:
Семейство interp функций: interp1, interp2, interp3 и interpn.
Класс griddedInterpolant.
И семейство interp функций и griddedInterpolant поддерживают основанную на сетке интерполяцию N-D. Однако существует память и выигрыши в производительности к использованию класса griddedInterpolant по функциям interp. Кроме того, класс griddedInterpolant обеспечивает один сопоставимый интерфейс для работы с данными с координатной сеткой в любом количестве размерностей.
Этот пример показывает, как функция interp1 может использоваться, чтобы интерполировать набор демонстрационных значений с помощью метода 'pchip'.
Функциональный interp1 выполняет одномерную интерполяцию. Его самая общая форма:
Vq = interp1(X,V,Xq,method)
где X является вектором координат, и V является вектором, содержащим значения в тех координатах. Xq является вектором, содержащим точки запроса, в которых можно интерполировать, и method опционально задает любой из четырех методов интерполяции: 'nearest', 'linear', 'pchip' или 'spline'.
Создайте набор 1D узлов решетки X и соответствующие демонстрационные значения V.
X = [1 2 3 4 5]; V = [12 16 31 10 6];
Интерполируйте на более прекрасных интервалах с 0,1 интервалами.
Xq = (1:0.1:5);
Vq = interp1(X,V,Xq,'pchip');Постройте выборки и интерполированные значения.
plot(X,V,'o'); hold on plot(Xq,Vq,'-'); legend('samples','pchip'); hold off

Этот пример показывает, как использовать опцию 'extrap', чтобы интерполировать вне области ваших точек выборки.
Задайте точки выборки и значения.
X = [1 2 3 4 5]; V = [12 16 31 10 6];
Задайте точки запроса, Xq, которые расширяют вне области X.
Xq = (0:0.1:6); Vq = interp1(X,V,Xq,'pchip','extrap');
Постройте график результатов.
figure plot(X,V,'o'); hold on plot(Xq,Vq,'-'); legend('samples','pchip'); hold off

В альтернативном подходе можно ввести дополнительные точки, чтобы получить больше контроля над поведением в экстраполируемых областях. Например, можно ограничить кривую оставаться плоской в экстраполируемой области путем расширения области с повторными значениями.
X = [0 1 2 3 4 5 6]; V = [12 12 16 31 10 6 6];
Задайте точки запроса, Xq, которые расширяют далее вне области X.
Xq = (-1:0.1:7);
Интерполируйте использование 'pchip'. Можно не использовать опцию 'extrap', потому что это - значение по умолчанию с 'pchip', 'makima' и методами 'spline'.
Vq = interp1(X,V,Xq,'pchip');Постройте график результатов.
figure plot(X,V,'o'); hold on plot(Xq,Vq,'-'); legend('samples','pchip'); hold off

Этот пример показывает, как функция interp2 может использоваться, чтобы интерполировать грубо выбранную функцию peaks по более прекрасной сетке.
interp2 и функции interp3 выполняют два и 3D интерполяция соответственно, и они интерполируют сетки в формате meshgrid. Синтаксис вызова для interp2 имеет общую форму:
Vq = interp2(X,Y,V,Xq,Yq,method)
где X и Y являются массивами координат, которые задают сетку в формате meshgrid, и V является массивом, содержащим значения в узлах решетки. Xq и Yq являются массивами, содержащими координаты точек запроса, в которых можно интерполировать. method опционально задает любой из четырех методов интерполяции: 'nearest', 'linear', 'cubic' или 'spline'.
Узлы решетки, которые включают X и Y, должны монотонно увеличиваться и должны соответствовать формату meshgrid.
Создайте крупную сетку и соответствующие демонстрационные значения.
[X,Y] = meshgrid(-3:1:3); V = peaks(X,Y);
Постройте демонстрационные значения.
surf(X,Y,V)
title('Sample Grid');
Сгенерируйте более прекрасную сетку для интерполяции.
[Xq,Yq] = meshgrid(-3:0.25:3);
Используйте interp2, чтобы интерполировать в точках запроса.
Vq = interp2(X,Y,V,Xq,Yq,'linear');Постройте график результатов.
surf(Xq,Yq,Vq);
title('Refined Grid');
Этот пример показывает, как использовать interp3, чтобы интерполировать 3-D функцию в едином запросе, указывают и сравнивают его со значением, сгенерированным аналитическим выражением.
interp3 работает таким же образом interp2 за исключением того, что требуется два дополнительных аргумента: один для третьей размерности в демонстрационной сетке и другом для третьей размерности в точках запроса,
Vq = interp3(X,Y,Z,V,Xq,Yq,Zq,method).
Как имеет место с interp2, узлы решетки, которые вы предоставляете к interp3, должны монотонно увеличиваться и должны соответствовать формату meshgrid.
Задайте функцию, которая генерирует значения для X, Y, и вход Z.
generatedvalues = @(X,Y,Z)(X.^2 + Y.^3 + Z.^4);
Создайте выборочные данные.
[X,Y,Z] = meshgrid((-5:.25:5)); V = generatedvalues(X,Y,Z);
Интерполируйте в определенной точке запроса.
Vq = interp3(X,Y,Z,V,2.35,1.76,0.23,'cubic')Vq = 10.9765
Сравните Vq со значением, сгенерированным аналитическим выражением.
V_actual = generatedvalues(2.35,1.76,0.23)
V_actual = 10.9771
Этот пример показывает, как функция interpn может использоваться, чтобы интерполировать грубо выбранную функцию по более прекрасной сетке с помощью метода 'cubic'.
Функциональный interpn выполняет n-мерную интерполяцию на сетках, которые находятся в формате ndgrid. Его самая общая форма:
Vq = interpn(X1,X2,X3,...Xn,V,Y1,Y2,Y3,...,Yn,method)
где X1,X2,X3,...,Xn является массивами координат, которые задают сетку в формате ndgrid, и V является массивом, содержащим значения в узлах решетки. Y1,Y2,Y3,...,Yn является массивами, содержащими координаты точек запроса, в которых можно интерполировать. method опционально задает любой из четырех методов интерполяции: 'nearest', 'linear', 'cubic' или 'spline'.
Узлы решетки, которые включают X1,X2,X3,...Xn, должны монотонно увеличиваться и должны соответствовать формату ndgrid.
Создайте набор узлов решетки и соответствующих демонстрационных значений.
[X1,X2] = ndgrid((-5:1:5)); R = sqrt(X1.^2 + X2.^2)+ eps; V = sin(R)./(R);
Постройте демонстрационные значения.
mesh(X1,X2,V)
title('Sample Grid');
Создайте более прекрасную сетку для интерполяции.
[Y1,Y2] = ndgrid((-5:.5:5));
Интерполируйте по более прекрасной сетке и постройте результаты.
Vq = interpn(X1,X2,V,Y1,Y2,'cubic'); mesh(Y1,Y2,Vq) title('Refined Grid');

interpn имеет альтернативный синтаксис: Vq = interpn(V,ntimes,method), который позволяет вам интерполировать по сетке, которая является целым числом времен, более прекрасных, чем демонстрационная сетка. В предыдущем коде Y1 и Y2 запросили interpolant по сетке, которая содержала одно дополнительное очко между каждой из выборок. Следующий код демонстрирует, как можно достигнуть того же результата с ntimes=1.
Интерполируйте по более прекрасной сетке с помощью ntimes=1.
Vq = interpn(V,1,'cubic');Постройте результат.
mesh(Vq)
title('Refined Grid with NTIMES');
Заметьте, что график масштабируется по-другому, чем в предыдущем примере. Это вызвано тем, что мы вызвали mesh и передали значения только. Функция mesh использовала сетку по умолчанию на основе размерностей Vq. Выходные значения являются тем же самым в обоих случаях.
Можно также предоставить нерегулярную координатную сетку точек запроса. Это может быть полезно, если вы интересуетесь запросом interpolant в более высоком разрешении в одной области сетки. Следующий код показывает, как это может быть сделано.
Интерполируйте по смещенной сетке.
[Y1, Y2] = ndgrid([-5 -4 -3 -2.5 -2 -1.5 -1.25 -1 -0.75 -0.5 -0.20 0]);
Vq = interpn(X1,X2,V,Y1,Y2,'cubic');Постройте результат.
mesh(Y1,Y2,Vq);
title('Biased Grid');
Как функция interpn, класс griddedInterpolant обеспечивает один интерфейс для основанной на сетке интерполяции в размерностях n. Однако griddedInterpolant предлагает следующие дополнительные выгоды:
Это предлагает существенные повышения производительности для повторных запросов к interpolant.
Это предлагает дополнительные повышения производительности и сбережения в потреблении памяти, потому что это хранит точки выборки как компактную сетку.
griddedInterpolant принимает выборочные данные, которые соответствуют формату ndgrid. Если вы хотите создать griddedInterpolant с данными meshgrid, необходимо будет преобразовать данные в формат ndgrid. Смотрите Преобразование meshgrid Данные к ndgrid Формату для демонстрации того, как преобразовать 2D и 3-D meshgrids.
Класс griddedInterpolant поддерживает методы интерполяции, которые также поддержаны interpn: nearest, linear, pchip, cubic, makima и spline. Однако griddedInterpolant предлагает большую производительность с меньше служебным.
interpolant является функцией, которая выполняет интерполяцию. Вы создаете interpolant путем вызова конструктора griddedInterpolant и передачи выборочных данных: сетка и соответствующие демонстрационные значения. Можно также задать метод интерполяции, если вы хотите заменить “линейный” метод по умолчанию. Синтаксис вызова имеет следующие формы:
Для 1D интерполяции можно передать x, набор точек, и v, вектор той же длины, содержащей соответствующие значения.
F = griddedInterpolant(x,v)
Для более высоких размерностей можно предоставить полную сетку. X1,X2,...,Xn задает сетку как набор n n-D массивы. Эти массивы соответствуют формату ndgrid и одного размера как демонстрационный массив V.
F = griddedInterpolant(X1,X2,...,Xn,V)
Если вы знаете, что расстояния между смежными точками выборки универсальны, можно позволить griddedInterpolant создать сетку по умолчанию путем передачи только точек выборки V.
F = griddedInterpolant(V)
Можно также задать координаты выборочных данных как компактная сетка. Компактная сетка представлена набором векторов. Эти векторы затем группированы в массив ячеек путем включения их в фигурных скобках; например, {x1g,x2g,...,xng}, где векторы x1g,x2g,...,xng задают декартовы координаты в каждой размерности.
F = griddedInterpolant({x1g,x2g,...,xng},V)Можно также задать метод интерполяции как итоговый входной параметр с любым из синтаксисов вызова. Этот пример задает самую близкую соседнюю интерполяцию.
F = griddedInterpolant({x1g,x2g,x3g},V,'nearest')
griddedInterpolant, F, оценен таким же образом, когда вы вызвали бы функцию. Ваши точки запроса могут быть рассеяны или с координатной сеткой, и можно передать их F любым из следующих способов:
Можно задать m-by-n матричный Xq, который содержит рассеянные точки m в размерностях n. Интерполированные значения Vq возвращены как m-by-1 вектор.
Vq = F(Xq)
Можно также задать точки запроса как серию вектор-столбцов n x1q,x2q,...,xnq длины m. Эти векторы представляют точки m в размерностях n. Интерполированные значения Vq возвращены как m-by-1 вектор.
Vq = F(x1q,x2q,...,xnq)
Можно задать точки запроса как серию n n - размерные массивы, представляющие полную сетку. Массивы X1q,X2q,...,Xnq является всем одинаковым размер и соответствует формату ndgrid. Интерполированные значения Vq также будут одного размера.
Vq = F(X1q,X2q,...,Xnq)
Можно также задать точки запроса как компактную сетку. x1gq,x2gq,...,xngq является векторами, которые задают узлы решетки в каждой размерности.
Vq = F({x1gq,x2gq,...,xngq})Например, в 2D:
Vq = F({(0:0.2:10),(-5:0.5:5)});
Класс griddedInterpolant признает, что ndgrid отформатировал выборочные данные. Если вы хотите создать griddedInterpolant с данными meshgrid, необходимо преобразовать их в формат ndgrid сначала.
Следующий пример обрисовывает в общих чертах шаги для преобразования 2D данных meshgrid к формату ndgrid. Мы начинаем путем создания meshgrid и соответствующих демонстрационных значений:
[X,Y] = meshgrid(-2:.1:2,-1:.1:1); V=0.75*Y.^3-3*Y-2*X.^2;
Чтобы преобразовать X, Y и V к формату ndgrid, выполняют эти шаги:
Транспонируйте каждый массив в сетке, а также выборочных данных.
X=X'; Y=Y'; V=V';
Теперь создайте interpolant.
F = griddedInterpolant(X,Y,V);
Чтобы преобразовать 3-D meshgrid, используйте функцию permute. Снова, запустите путем создания meshgrid и соответствующих демонстрационных значений:
[X,Y,Z] = meshgrid(-5:5,-3:3,-10:10); V = X.^3 + Y.^2 + Z;
Чтобы преобразовать X, Y, Z и V к формату ndgrid, выполняют эти шаги:
Используйте функцию permute, чтобы обменяться строками и столбцами каждого массива. Результирующий эффект будет транспонированием каждой страницы.
P = [2 1 3]; X = permute(X,P); Y = permute(Y,P); Z = permute(Z,P); V = permute(V,P);
Теперь создайте interpolant.
F = griddedInterpolant(X,Y,Z,V);
Этот пример показывает, как создать и построить 1D interpolant использование griddedInterpolant с методом кубичной интерполяции.
Создайте крупную сетку и демонстрационные значения.
X = [1 2 3 4 5]; V = [12 6 15 9 6];
Создайте griddedInterpolant с помощью метода кубичной интерполяции.
F = griddedInterpolant(X,V,'cubic')F =
griddedInterpolant with properties:
GridVectors: {[1 2 3 4 5]}
Values: [12 6 15 9 6]
Method: 'cubic'
ExtrapolationMethod: 'cubic'
Свойство GridVectors содержит компактную сетку, задающую координаты демонстрационных значений V. Свойство Method задает метод интерполяции. Заметьте, что мы задали 'cubic', когда мы создали F. Если вы не используете аргумент Method, метод интерполяции по умолчанию, linear, будет присвоен F.
Можно получить доступ к любому из свойств F таким же образом, вы получили бы доступ к полям в struct.
F.GridVectors; % Displays the grid vectors as a cell array F.Values; % Displays the sample values F.Method; % Displays the interpolation method
Интерполируйте на более прекрасных интервалах с 0,1 интервалами.
Xq = (1:0.1:5); Vq = F(Xq);
Постройте результат.
plot(X,V,'o'); hold on plot(Xq,Vq,'-'); legend('samples','Cubic Interpolation');

Этот пример показывает, как создать и построить 2D interpolant использование griddedInterpolant.
В двух измерениях и выше, можно задать демонстрационные координаты как ndgrid, компактную сетку или сетку по умолчанию. В этом примере мы предоставим ndgrid.
Создайте крупную сетку и демонстрационные значения.
[X,Y] = ndgrid(-1:.3:1,-2:.3:2); V = 0.75*Y.^3 - 3*Y - 2*X.^2;
Создайте griddedInterpolant.
F = griddedInterpolant(X,Y,V,'spline');Интерполируйте на более прекрасных интервалах с 0,1 интервалами.
[Xq,Yq] = ndgrid(-1:.1:1,-2:.1:2); Vq = F(Xq,Yq);
Постройте результат.
figure()
surf(X,Y,V);
view(65,60)
title('Sample Data');
figure()
surf(Xq,Yq,Vq);
view(65,60)
title('Refined with Spline');
Этот пример показывает, как создать 3-D interpolant и оценить по плоскости разбиения, таким образом, можно построить значения на той плоскости.
Создайте полную сетку и демонстрационные значения.
[X,Y,Z] = ndgrid((-5:2:5)); V = X.^3 + Y.^2 + Z.^2;
Создайте griddedInterpolant.
F = griddedInterpolant(X,Y,Z,V,'cubic');Поскольку мы уже создали полную сетку, чтобы сгенерировать наши демонстрационные значения, нам была нечего терять мимоходом она к griddedInterpolant. На практике однако распространено загрузить выборочные данные в MATLAB от диска. Компактная сетка может очень выгодный в таких случаях, потому что она позволяет вам задавать целую сетку в форме, которая намного более экономична с точки зрения памяти. Если бы мы загрузили V в MATLAB вместо того, чтобы вычислить его от полной сетки, мы, возможно, создали компактную сетку, чтобы сохранить память в нашей рабочей области. Например,
gv = {(-5:2:5),(-5:2:5),(-5:2:5)};
F = griddedInterpolant(gv,V,'cubic');Теперь интерполируйте по плоскости в Z = 2 с 0,25 интервалами.
[Xq,Yq,Zq] = ndgrid((-5:.25:5),(-5:.25:5),2:2); Vq = F(Xq,Yq,Zq);
Постройте результат.
surf(Xq,Yq,Vq);
title('Refined with Linear Interpolation');
Этот пример создает 4-D interpolant и оценивает его в одной точке.
Создайте крупную сетку и демонстрационные значения.
[X1,X2,X3,X4] = ndgrid((-5:2:5)); V = X1.^3 + X2.^2 + X3.^2 +X4;
Создайте griddedInterpolant.
F = griddedInterpolant(X1,X2,X3,X4,V,'linear');
Запросите griddedInterpolant в одной точке.
Vq = F([-3.2 2.1 4.7 -1.3])
MATLAB выводит следующее:
ans = -10.1000
.
В зависимости от расположения ваших точек запроса можно предпочесть один синтаксис оценки по другим. Например, создайте следующий interpolant:
[X,Y] = ndgrid(-1:.25:1,-2:.25:2); V = 0.75*Y.^3-3*Y-2*X.^2; F = griddedInterpolant(X,Y,V);
Запросите F с помощью полной сетки, чтобы дать значения в узлах решетки:
[Xq,Yq] = ndgrid(-1:.1:0,-2:.1:0); Vq = F(Xq,Yq);
Можно также интерполировать по той же сетке с помощью компактного формата сетки:
gvq = {-1:.1:0,-2:.1:0};
Vq = F(gvq);Или можно запросить одну точку:
Vq = F(.315,.738)
который возвращается:
Vq = -2.1308
или случайный набор рассеянных точек:
rng('default')
Vq = F(rand(3,2))который возвращается:
Vq = -3.4919 -3.3557 -0.3515
Можно также исследовать Values в F:
F.Values(1,3)
который возвращается:
ans = -0.0313
Или можно заменить массив Values:
F.Values = 2*V;
Можно отредактировать свойства в F на лету. Например, можно заменить метод интерполяции можно следующим образом:
F.Method = 'cubic';
Можно также заменить GridVectors в F. Во-первых, исследуйте GridVectors:
gv = F.GridVectors;
gv{1}gv является массивом ячеек, и gv{1} отображает первый вектор сетки: ans = -1.0000 -0.7500 -0.5000 -0.2500 0 0.2500 0.5000 0.7500 1.0000
Теперь замените GridVectors в F путем создания нового массива ячеек new_gv:
new_gv = {(0:0.3:1),(0:0.3:1)};
F.GridVectors = new_gv;