Возвращаемое значение на основе интерполяции набора точек данных
tablelookup(x1d, x2d, x3d, x4d, fd, x1, x2, x3, x4,
interpolation = linear|smooth, extrapolation = linear|nearest|error)
Используйте функцию tablelookup в разделе equations, чтобы вычислить выходное значение путем интерполяции входного значения против набора точек данных. Эта функциональность подобна тому из Simulink® и блоков Интерполяционной таблицы Simscape™. Это позволяет вам включать табличное моделирование непосредственно в ваш авторский блок без потребности соединения внешнего блока Lookup Table к вашей модели.
Поддержки функции tablelookup одномерные, двумерные, 3D, и четырехмерные интерполяционные таблицы. Полный синтаксис:
tablelookup(x1d, x2d, x3d, x4d, fd, x1, x2, x3, x4,
interpolation = linear|smooth, extrapolation = linear|nearest|error)
|
|
Набор данных входных значений вдоль первого направления, заданного как одномерный массив. Значения должны быть строго монотонными, или увеличение или уменьшение. Это - обязательный аргумент. |
|
|
Набор данных входных значений вдоль второго направления, заданного как одномерный массив. Значения должны быть строго монотонными, или увеличение или уменьшение. Этот аргумент используется только для двумерного и 3D поиска по таблице. |
|
|
Набор данных входных значений вдоль третьего направления, заданного как одномерный массив. Значения должны быть строго монотонными, или увеличение или уменьшение. Этот аргумент используется только для 3D поиска по таблице. |
|
|
Набор данных входных значений вдоль четвертого направления, заданного как одномерный массив. Значения должны быть строго монотонными, или увеличение или уменьшение. Этот аргумент используется только для 3D поиска по таблице. |
|
|
Набор данных выходных значений для поиска по таблице. Это - обязательный аргумент. Для одномерного поиска по таблице Для двумерного поиска по таблице Для 3D поиска по таблице Для четырехмерного поиска по таблице |
|
|
Входное значение вдоль первого направления. Его модули должны быть соразмерными с модулями |
|
|
Входное значение вдоль второго направления. Его модули должны быть соразмерными с модулями |
|
|
Входное значение вдоль третьего направления. Его модули должны быть соразмерными с модулями |
|
|
Входное значение вдоль четвертого направления. Его модули должны быть соразмерными с модулями |
|
|
Дополнительный аргумент, который задает метод приближения для вычисления выходного значения, когда входное значение в области значений, заданной в интерполяционной таблице. Значением по умолчанию является |
|
|
Дополнительный аргумент, который задает метод приближения для вычисления выходного значения, когда входное значение вне области значений, заданной в интерполяционной таблице. Значением по умолчанию является |
Значения аргументов interpolation:
linear — Для одномерного поиска по таблице, использует линейную функцию. Для двумерного и 3D поиска по таблице, использует расширение линейного алгоритма для многомерной интерполяции, путем выполнения линейной интерполяции в первом направлении, затем во втором направлении, и затем в третьем направлении. Используйте этот метод, чтобы получить лучшую производительность.
smooth — Использует измененный алгоритм Акима, описанный в Сглаженном Алгоритме Интерполяции. Используйте этот метод, чтобы произвести непрерывную кривую или поверхность с непрерывными производными первого порядка.
Значения аргументов extrapolation:
linear — Расширяет от ребра области интерполяции линейно. Наклон линейной экстраполяции равен наклону интерполированной кривой или поверхности в ребре области интерполяции. Используйте этот метод, чтобы произвести кривую или поверхность с непрерывным значением и непрерывными производными первого порядка на контуре между областью интерполяции и областью экстраполяции.
самый близкий Расширяет от ребра области интерполяции как константа. Значение самой близкой экстраполяции равно значению интерполированной кривой или поверхности в ребре области интерполяции. Используйте этот метод, чтобы произвести кривую или поверхность с непрерывным значением на контуре между областью интерполяции и областью экстраполяции, которая не выходит за предел самой высокой точки в данных или ниже самой низкой точки в данных.
ошибка Генерирует ошибку, когда входное значение вне области значений, заданной в интерполяционной таблице.
Функция возвращает выходное значение, в модулях, заданных для fd, путем поиска или оценки табличных значений на основе входных значений:
Когда входные параметры x1, x2, x3 и x4... | Функция tablelookup... |
|---|---|
Совпадайте со значениями в наборах входных данных, x1d, x2d, x3d и x4d | Выводит соответствующее табличное значение, fd |
| Не совпадайте со значениями в наборах входных данных, но в области значений | Интерполирует соответствующие табличные значения, с помощью метода, заданного как значение аргумента interpolation |
| Не совпадайте со значениями в наборах входных данных, и вне области значений | Экстраполирует выходное значение, с помощью метода, заданного как значение аргумента extrapolation |
Следующие правила применяются к наборам данных x1d, x2d, x3d, x4d и fd:
Для одномерного поиска по таблице x1d и fd должны быть одномерными массивами, одного размера.
Для двумерного поиска по таблице x1d и x2d должны быть одномерными массивами, и fd должен быть матрицей с размером, совпадающим с размерностями, заданными наборами входных данных. Например, если x1d является 1 m массивом, и x2d является 1 n массивом, то fd должен быть m-by-n матрица.
Для 3D поиска по таблице x1d, x2d и x3d должны быть одномерными массивами, и fd должен быть 3D массивом с размером, совпадающим с размерностями, заданными наборами входных данных. Например, если x1d является 1 m массивом, x2d является 1 n массивом, и x3d является 1 p массивом, то fd должен быть m-by-n-by-p массив.
Для четырехмерного поиска по таблице x1d, x2d, x3d и x4d должны быть одномерными массивами, и fd должен быть четырехмерным массивом с размером, совпадающим с размерностями, заданными наборами входных данных. Например, если x1d является 1 m массивом, x2d является 1 n массивом, x3d является 1 p массивом, и x4d является 1 q массивом, то fd должен быть m-by-n-by-p-by-q массив.
x1d, x2d, x3d и значения x4d должны быть строго монотонными, или увеличение или уменьшение.
Для сглаженной интерполяции каждый набор данных входных значений должен содержать по крайней мере три значения. Для линейной интерполяции два значения достаточны.
Библиотека Foundation включает встроенные перечисления, interpolation.m и extrapolation.m:
classdef interpolation < int32
enumeration
linear (1)
smooth (2)
end
methods(Static)
function map = displayText()
map = containers.Map;
map('linear') = 'Linear';
map('smooth') = 'Smooth';
end
end
endclassdef extrapolation < int32
enumeration
linear (1)
nearest (2)
error (3)
end
methods(Static)
function map = displayText()
map = containers.Map;
map('linear') = 'Linear';
map('nearest') = 'Nearest';
map('error') = 'Error';
end
end
endЭти перечисления расположены в директории matlabroot \toolbox\physmod\simscape\library\m\+simscape\+enum.
Можно использовать эти перечисления, чтобы объявить параметры компонента, и затем использовать эти параметры в качестве аргументов функции tablelookup. Для получения дополнительной информации смотрите Заданный Пользователями пример Методов Интерполяции и Экстраполяции и Используя Перечисление в Аргументах функции.
Этот пример реализует одномерную интерполяционную таблицу с линейной интерполяцией и экстраполяцией.
component tlu_1d_linear inputs u = 0; end outputs y = 0; end parameters (Size=variable) xd = [1 2 3 4]; yd = [1 2 3 4]; end equations y == tablelookup(xd, yd, u); end end
xd и yd объявляются как параметры переменного размера. Это позволяет пользователям блока обеспечить свои собственные наборы данных, когда компонент преобразован в авторский блок. Для получения дополнительной информации смотрите Используя Интерполяционные таблицы в уравнениях.
Значения xd должны быть строго монотонными, или увеличение или уменьшение. yd должен иметь тот же размер как xd.
Этот пример реализует двумерную интерполяционную таблицу с определенными методами интерполяции и экстраполяции.
component tlu_2d inputs u1 = 0; u2 = 0; end outputs f = 0; end parameters (Size=variable) x1d = [1 2 3 4]; x2d = [1 2 3]; fd = [1 2 3; 3 4 5; 5 6 7; 7 8 9]; end equations f == tablelookup(x1d, x2d, fd, u1, u2, interpolation=smooth, extrapolation=nearest); end end
x1d, x2d и fd объявляются как параметры переменного размера. x1d и значения вектора x2d должны быть строго монотонными, или увеличение или уменьшение. Для сглаженной интерполяции каждый вектор должен иметь по крайней мере три значения. Размер матрицы fd должен совпадать с размерностями векторов x2d и x1d.
Интерполяция использует измененный алгоритм Акима, как описано в Сглаженном Алгоритме Интерполяции. Экстраполяция использует самое близкое значение fd для u1 из области значений и значения u2.
Этот пример подобен предыдущему, но это дает контроль за работой пользователей блока по методам интерполяции и экстраполяции.
import simscape.enum.* component tlu_2d_enum inputs u1 = 0; u2 = 0; end outputs f = 0; end parameters (Size=variable) x1d = [1 2 3 4]; x2d = [1 2 3]; fd = [1 2 3; 3 4 5; 5 6 7; 7 8 9]; end parameters interp = interpolation.linear; % Interpolation method extrap = extrapolation.linear; % Extrapolation method end equations f == tablelookup(x1d, x2d, fd, u1, u2, interpolation=interp, extrapolation=extrap); end end
Компонент импортирует встроенные перечисления, и затем использует их, чтобы объявить два дополнительных параметра: interp (Interpolation method) и extrap (Extrapolation method). Функция tablelookup использует эти параметры в качестве аргументов, чтобы задать методы интерполяции и экстраполяции. Для получения дополнительной информации смотрите Используя Перечисление в Аргументах функции.
Блок, сгенерированный от этого компонента, будет иметь Interpolation method и параметры Extrapolation method, обоих со значением по умолчанию Linear. Пользователь блока может выбрать любые другие опции интерполяции и экстраполяции.
Этот пример реализует одномерную интерполяционную таблицу с модулями, чтобы сопоставить температуру с давлением, с линейной интерполяцией и экстраполяцией.
component TtoP
inputs
u = {0, 'K'}; % temperature
end
outputs
y = {0, 'Pa'}; % pressure
end
parameters (Size=variable)
xd = {[100 200 300 400] 'K'};
yd = {[1e5 2e5 3e5 4e5] 'Pa'};
end
equations
y == tablelookup(xd, yd, u);
end
end
xd и yd объявляются как параметры переменного размера с модулями. Это позволяет пользователям блока обеспечить свои собственные наборы данных, когда компонент преобразован в авторский блок, и также выбрать соразмерные модули из раскрытия в диалоговом окне авторского блока. Для получения дополнительной информации смотрите Используя Интерполяционные таблицы в уравнениях.
Значения xd должны быть строго монотонными, или увеличение или уменьшение. yd должен иметь тот же размер как xd.
Для сглаженной интерполяции функция использует измененный алгоритм Акима. Для одномерной сглаженной интерполяции алгоритм Акима, описанный в [1], производит непрерывную кривую с непрерывными производными первого порядка. Это также пытается сохранить наклон и избежать волнистостей, где данные предлагают плоскую область.
Алгоритм интерпретирует данные как плоскую область каждый раз, когда существует три или больше последовательных колинейных точки в табличных данных. Это затем соединяет те три или больше точки с прямой линией. Колинейные точки не должны быть горизонталью. Чтобы гарантировать, что область между двумя точками данных является плоской, вставьте дополнительную точку данных между теми двумя точками.
Следующие графические показы различие между Акима и интерполяцией сплайна.
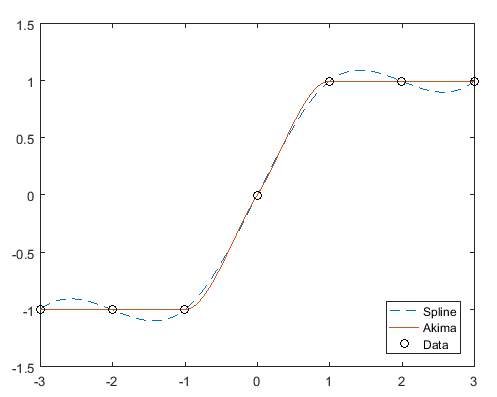
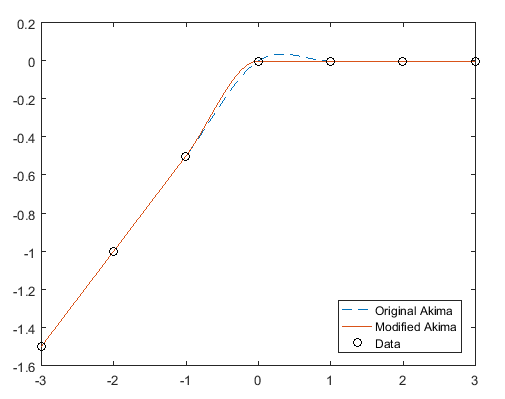
Когда две плоских области с различными наклонами встречаются, не возможно избежать волнистости при поддержании гладкости. Исходный алгоритм Акима дает равные веса точкам с обеих сторон, таким образом равномерно деля волнистость. Измененный алгоритм, используемый в этой функции, дает больше веса стороне, где наклон ближе к нулю. Эта модификация уделяет первостепенное значение стороне, которая ближе к горизонтали, которая более интуитивна (см. затем графический).
Для многомерной интерполяции метод Акима расширен путем вычисления смешанных производных в узлах решетки с помощью взвешенного среднего конечных разностей, как описано в [2].
[1] Акима, Хироши. "Новый метод интерполяции и плавной кривой, соответствующей на основе локальных процедур". Журнал ACM (JACM), 17.4, 1970, стр 589-602.
[2] Акима, Хироши. "Метод двумерной интерполяции и сглаженной поверхности, соответствующей на основе локальных процедур". Коммуникации ACM, 17.1, 1974, стр 18-20.
Интерполяционная таблица PS (1D) | (2D) интерполяционная таблица PS | (3D) интерполяционная таблица PS | Интерполяционная таблица PS (4D) | equations