Этот пример показывает, как моделировать управляемые силой тяжести орбиты главных тел солнечной системы. Модель обрабатывает солнце и планеты как совершенные сферы каждый с тремя переводными степенями свободы. Вращение планеты проигнорировано. Поля тяготения генерируют силы, которые сохраняют планеты в орбите.

Твердые блоки представляют тела солнечной системы и обеспечивают их конфигурации, инерцию и цвета. Декартовы Объединенные блоки задают степени свободы тел относительно мирового кадра, расположенного в барицентре солнечной системы. Блоки Поля тяготения добавляют силы дальние, ответственные за изгиб начальных траекторий планеты на закрытые эллиптические орбиты.
Декартовы Объединенные блоки обеспечивают начальные состояния — положения и скорости — солнца и планет относительно мирового кадра. Начальные состояния соответствуют настройке солнечной системы 20-го июня 2016. Они получены от эфемеридных баз данных, сохраняемых Лабораторией реактивного движения (JPL).
Можно запросить базы данных через систему Горизонтов JPL с помощью интерфейса telnet или сети. Пользователи Aerospace Toolbox могут альтернативно получить эфемеридные данные в командной строке MATLAB® с помощью функции planetEphemeris после установки Космического Эфемеридного пакета Информационной поддержки.
Откройте шаблон модели Simscape™ Multibody™ и удалите все ненужные блоки. Измените настройки силы тяжести так, чтобы можно было добавить поля тяготения в модель. Результат обеспечивает отправную точку для модели солнечной системы.
В подсказке команды MATLAB введите smnew. MATLAB открывает образцовый шаблон с обычно используемыми блоками и подходящими настройками решателя для моделей Simscape Multibody.
Сократите все кроме Настройки Механизма, Настройки Решателя и Мировых блоков Кадра. Эти три блока предоставляют модели настройки силы тяжести, настройки решателя и глобальный кадр ссылки инерции.
В диалоговом окне Блока Configuration Механизма, набор Uniform Gravity к None. Эта установка позволяет силе тяжести модели как сила закона обратных квадратов с помощью блоков Поля тяготения вместо этого.
Представляйте тела солнечной системы с помощью Твердых блоков. Задайте геометрию и параметры инерции с точки зрения переменных MATLAB и инициализируйте эти переменные в рабочем пространстве модели с помощью Model Explorer. Переменные являются структурами данных, названными в честь тел солнечной системы с помощью капитализации имени собственного.
Добавьте в модель девять Твердых блоков от библиотеки Body Elements. Блоки представляют солнце и восемь известных планет.
Соедините и назовите блоки как показано в фигуре. Разветвленная строка связи кадра между мировым кадром и планетами делает их твердо соединенными и совпадающими на пробеле. Вы позже изменяете это условие с помощью Декартовых Объединенных блоков.
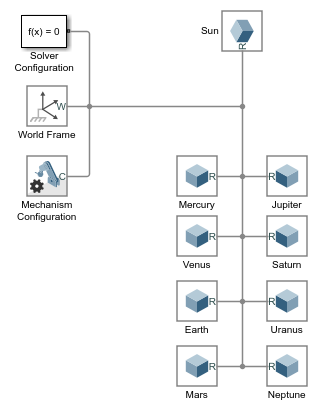
В диалоговых окнах блока Solid, набор Geometry> параметр Shape к Sphere и Inertia> параметр Based on к Mass. Установка параметра инерции позволяет вам задать твердую массу непосредственно так, чтобы можно было масштабировать формы планеты, не влияя на образцовую динамику.
Задайте следующие Твердые параметры блоков с точки зрения полей структуры данных MATLAB. Введите имена полей в формат Structure.Field, где Structure является именем случая заголовка тела солнечной системы, и Field является строкой, показанной в таблице — например, Sun.R или Earth.RGB.
| Параметры блоков | Полевая строка |
|---|---|
| Geometry> Radius | R |
| Inertia> Mass | M |
| Graphic> Visual Properties> Color | RGB |
Вы позже задаете новые поля структуры в рабочем пространстве модели с помощью Model Explorer.
В панели меню Simulink® выберите Tools> Model Explorer.
В панели Иерархии модели Model Explorer расширьте узел для своей модели и выберите Model Workspace. Панель Иерархии модели находится на левой стороне.
В панели Рабочего пространства модели Model Explorer, набор Data Source к MATLAB Code. Панель Рабочего пространства модели находится на правой стороне.
В поле MATLAB Code добавьте код инициализации для свойств тела солнца и планеты. Код организован в разделы, названные в честь тел солнечной системы. Вы позже добавляете данные об исходном положении и скорости в эти разделы.
% All values are in SI units. % RGB color vectors are on a normalized 0-1 scale. % Body dimensions are scaled for visualization purposes. % Scaling has no impact on model dynamics. % Scaling SunScaling = 0.5e2; TerrestrialPlanetScaling = 1.2e3; GasGiantScaling = 2.5e2; % Sun Sun.M = 1.99e30; Sun.R = 6.96e8*SunScaling; Sun.RGB = [1 0.5 0]; % Mercury Mercury.M =3.30e23; Mercury.R = 2.44e6*TerrestrialPlanetScaling; Mercury.RGB = [0.5 0.5 0.5]; % Venus Venus.M = 4.87e24; Venus.R = 6.05e6*TerrestrialPlanetScaling; Venus.RGB = [1 0.9 0]; % Earth Earth.M = 5.97e24; Earth.R = 6.05e6*TerrestrialPlanetScaling; Earth.RGB = [0.3 0.6 0.8]; % Mars Mars.M = 6.42e23; Mars.R = 3.39e6*TerrestrialPlanetScaling; Mars.RGB = [0.6 0.2 0.4]; % Jupiter Jupiter.M = 1.90e27; Jupiter.R = 6.99e7*GasGiantScaling; Jupiter.RGB = [0.6 0 0.3]; % Saturn Saturn.M = 5.68e26; Saturn.R = 5.82e7*GasGiantScaling; Saturn.RGB = [1 1 0]; % Uranus Uranus.M = 8.68e25; Uranus.R = 2.54e7*GasGiantScaling; Uranus.RGB = [0.3 0.8 0.8]; % Neptune Neptune.M = 1.02e26; Neptune.R = 2.46e7*GasGiantScaling; Neptune.RGB = [0.1 0.7 0.8];
Нажмите Reinitialize from Source.
Твердые блоки теперь имеют все числовые данные, они должны представить формы планеты и цвета. Попытайтесь открыть диалоговое окно блока Solid и проверьте, что сфера теперь появляется в твердой панели визуализации.
Заземлите серьезную визуализацию

Добавьте три переводных степени свободы между барицентром солнечной системы и каждым телом солнечной системы с помощью Декартовых Объединенных блоков. Вы дальнейшее использование эти блоки, чтобы задать исходные положения и скорости тел солнечной системы.
Добавьте в модель девять Декартовых Объединенных блоков от библиотеки Joints. Блоки обеспечивают переводные степени свободы солнца и восьми известных планет.
Соедините и назовите блоки как показано в фигуре. Если вы помещаете блок в существующую строку связи, программное обеспечение Simscape Multibody автоматически соединяет блок с той строкой. Инвертируйте и поверните объединенные блоки, чтобы гарантировать, что Твердые блоки соединяют только с последователем (F) порты кадра.
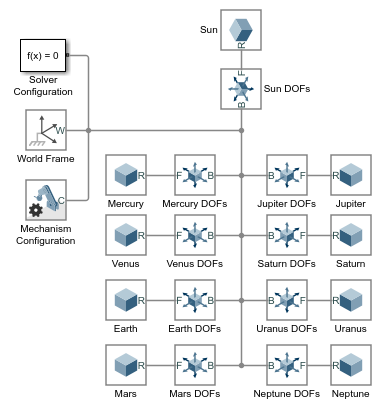
Солнце и планеты твердо больше не соединяются. Они могут теперь перевести друг относительно друга. Они являются, однако, все еще совпадающими на пробеле. Чтобы разместить их в различных исходных положениях и дать им начальные скорости, необходимо задать объединенные цели состояния.
Задайте начальные состояния солнца и планеты с точки зрения переменных MATLAB с помощью Декартовых Объединенных блоков в модели. Затем инициализируйте новые переменные MATLAB в рабочем пространстве модели с помощью Model Explorer. Вы задаете переменные MATLAB как новые поля в существующих структурах данных.
В диалоговых окнах блока Cartesian Joint проверяйте флажки State Targets> Specify Position Target и State Targets> Specify Velocity Target на эти X, Y, и призматические объединенные примитивы Z. Эти настройки позволяют вам задать желаемые начальные состояния солнца и планет.
Задайте Декартовы Объединенные целевые значения состояния для этих X, Y, и призматические объединенные примитивы Z с точки зрения полей структуры MATLAB. Введите имена полей в формат Structure.Field, где Structure является именем случая заголовка тела солнечной системы, и Field является строкой, показанной в таблице — например, Sun.Px или Earth.Vz.
| Соедините примитивную ось | Цель состояния | Полевая строка |
|---|---|---|
| X | Положение | Px |
| Скорость | Vx | |
| Y | Положение | Py |
| Скорость | Vy | |
| Z | Положение | Pz |
| Скорость | Vz |
Вы позже задаете новые поля структуры в рабочем пространстве модели с помощью Model Explorer.
В панели меню Simulink выберите Tools> Model Explorer.
В панели Иерархии модели Mechanics Explorer расширьте узел для своей модели и выберите Model Workspace. Панель Иерархии модели находится на левой стороне.
В панели Рабочего пространства модели Model Explorer, набор Data Source к MATLAB Code. Панель Рабочего пространства модели находится на правой стороне.
В поле MATLAB Code добавьте код инициализации для объединенных целей состояния. Новый код, отображенный синим, состоит из компонентов положения и скорости, полученных из эфемеридных баз данных JPL. Можно скопировать только новый код или заменить целый код рабочего пространства модели на показанный.
% All values are in SI units. % RGB color vectors are on a normalized 0-1 scale. % Body dimensions are scaled for visualization purposes. % Scaling has no impact on model dynamics. % Scaling SunScaling = 0.5e2; TerrestrialPlanetScaling = 1.2e3; GasGiantScaling = 2.5e2; % Sun Sun.M = 1.99e30; Sun.R = 6.96e8*SunScaling; Sun.RGB = [1 0.5 0]; Sun.Px = 5.5850e+08; Sun.Py = 5.5850e+08; Sun.Pz = 5.5850e+08; Sun.Vx = -1.4663; Sun.Vy = 11.1238; Sun.Vz = 4.8370; % Mercury Mercury.M =3.30e23; Mercury.R = 2.44e6*TerrestrialPlanetScaling; Mercury.RGB = [0.5 0.5 0.5]; Mercury.Px = 5.1979e+10; Mercury.Py = 7.6928e+09; Mercury.Pz = -1.2845e+09; Mercury.Vx = -1.5205e+04; Mercury.Vy = 4.4189e+04; Mercury.Vz = 2.5180e+04; % Venus Venus.M = 4.87e24; Venus.R = 6.05e6*TerrestrialPlanetScaling; Venus.RGB = [1 0.9 0]; Venus.Px = -1.5041e+10; Venus.Py = 9.7080e+10; Venus.Pz = 4.4635e+10; Venus.Vx = -3.4770e+04; Venus.Vy = -5.5933e+03; Venus.Vz = -316.8994; % Earth Earth.M = 5.97e24; Earth.R = 6.05e6*TerrestrialPlanetScaling; Earth.RGB = [0.3 0.6 0.8]; Earth.Px = -1.1506e+09; Earth.Py = -1.3910e+11; Earth.Pz = -6.0330e+10; Earth.Vx = 2.9288e+04; Earth.Vy = -398.5759; Earth.Vz = -172.5873; % Mars Mars.M = 6.42e23; Mars.R = 3.39e6*TerrestrialPlanetScaling; Mars.RGB = [0.6 0.2 0.4]; Mars.Px = -4.8883e+10; Mars.Py = -1.9686e+11; Mars.Pz = -8.8994e+10; Mars.Vx = 2.4533e+04; Mars.Vy = -2.7622e+03; Mars.Vz = -1.9295e+03; % Jupiter Jupiter.M = 1.90e27; Jupiter.R = 6.99e7*GasGiantScaling; Jupiter.RGB = [0.6 0 0.3]; Jupiter.Px = -8.1142e+11; Jupiter.Py = 4.5462e+10; Jupiter.Pz = 3.9229e+10; Jupiter.Vx = -1.0724e+03; Jupiter.Vy = -1.1422e+04; Jupiter.Vz = -4.8696e+03; % Saturn Saturn.M = 5.68e26; Saturn.R = 5.82e7*GasGiantScaling; Saturn.RGB = [1 1 0]; Saturn.Px = -4.2780e+11; Saturn.Py = -1.3353e+12; Saturn.Pz = -5.3311e+11; Saturn.Vx = 8.7288e+03; Saturn.Vy = -2.4369e+03; Saturn.Vz = -1.3824e+03; % Uranus Uranus.M = 8.68e25; Uranus.R = 2.54e7*GasGiantScaling; Uranus.RGB = [0.3 0.8 0.8]; Uranus.Px = 2.7878e+12; Uranus.Py = 9.9509e+11; Uranus.Pz = 3.9639e+08; Uranus.Vx = -2.4913e+03; Uranus.Vy = 5.5197e+03; Uranus.Vz = 2.4527e+03; % Neptune Neptune.M = 1.02e26; Neptune.R = 2.46e7*GasGiantScaling; Neptune.RGB = [0.1 0.7 0.8]; Neptune.Px = 4.2097e+12; Neptune.Py = -1.3834e+12; Neptune.Pz = -6.7105e+11; Neptune.Vx = 1.8271e+03; Neptune.Vy = 4.7731e+03; Neptune.Vz = 1.9082e+03;
Нажмите Reinitialize from Source.
Модель теперь имеет числовые данные, это должно собрать планеты в координатах положения, полученных из баз данных JPL. Однако симуляция модели в этой точке показала бы планеты, перемещающиеся в прямолинейные траектории. Чтобы получить эллиптические орбиты, необходимо завершить модель путем добавления полей тяготения солнца и планеты.

Смоделируйте гравитацию каждого тела солнечной системы с помощью блока Gravitational Field. Этот блок автоматически вычисляет гравитацию тела на всех других телах с помощью закона Ньютона универсальной гравитации.
В каждом диалоговом окне блока Solid расширьте область Frames и нажмите кнопку Create.
Установите параметр Frame Name на R2 и нажмите кнопку Save. Новый кадр является точной копией ссылочного кадра, но имеет отдельный порт кадра. Можно использовать эти порты, чтобы соединить блоки поля тяготения при предотвращении пересеченных строк связи.
Добавьте в модель девять блоков Поля тяготения от библиотеки Forces и Torques. Блоки предоставляют гравитационным силам, которые каждое тело солнечной системы проявляет на всех других телах.
Соедините и назовите блоки как показано в фигуре. Гарантируйте, что блоки соединяются непосредственно с Твердыми блоками. Такая связь гарантирует, что поля сосредоточены на твердых сферах и твердо соединены с ними.
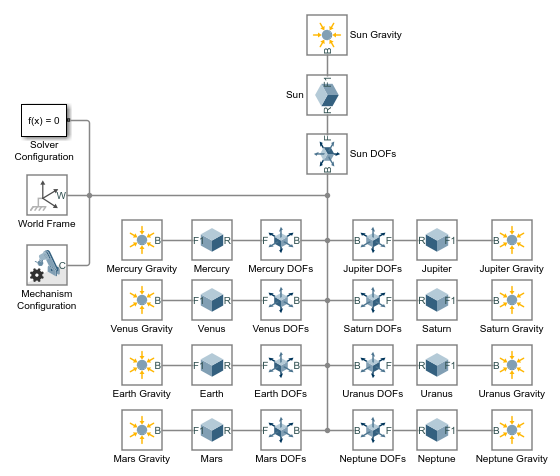
В блоках Поля тяготения задайте параметр Mass как имена полей структуры MATLAB. Введите имена полей в формат Structure.Field, где Structure является именем случая заголовка тела солнечной системы, и Field является строкой M — например, Sun.M или Earth.M. Эти поля были ранее заданы в рабочем пространстве модели.
Сконфигурируйте настройки решателя Simulink, чтобы получить десять наземных оборотов в одной симуляции. Затем моделируйте модель и просмотрите получившуюся анимацию солнечной системы. Сконфигурируйте настройки анимации, чтобы проигрывать десятилетнюю анимацию в период нескольких секунд.
В панели меню Simulink выберите Simulation> Model Configuration Parameters.
Установите параметр Stop time на 10*365*24*60*60. Этот номер, равный десяти годам в секундах, позволяет вам моделировать все десять земель обороты с 20-го июня 2016 до 20-го июня 2026.
Установите параметр Max step size на 24*60*60. Этот номер, равный одному дню в секундах, является достаточно маленьким, чтобы обеспечить результаты плавной анимации. Увеличьте это число, если вы предпочитаете более быстрые результаты симуляции.
Обновите блок-схему, например, путем выбора Simulation> Update Diagram. Mechanics Explorer открывается статическим 3-D отображением модели в ее начальном состоянии. Проверяйте, что солнце и планеты появляются в панели визуализации и что их относительные размерности и положения разумны.
Запустите симуляцию, например, путем выбора Simulation> Run. Mechanics Explorer проигрывает анимацию солнечной системы. Обратите внимание на то, что при основной скорости воспроизведения по умолчанию, планеты кажутся статичными. Необходимо увеличить эту скорость в настройках анимации Mechanics Explorer.
В Mechanics Explorer выберите Tools> Animation Settings.
В Base(1X) Playback Speed введите 3153600. Эта скорость соответствует одному наземному обороту каждые десять секунд.
Приостановите и проигрывайте анимацию, чтобы применить новую основную скорость воспроизведения. Данные показывают результаты анимации на новой скорости.

Можно открыть полную модель солнечной системы путем ввода smdoc_solar_system_wfield_b в подсказке команды MATLAB.