Этот пример показывает, как настроить электропривод с помощью структуры каскадного регулирования.
Данные показывают цикл управления с обратной связью, который использует структуру каскадного регулирования. Внешний контур регулировки скорости медленнее действует, чем внутренний контур управления током.
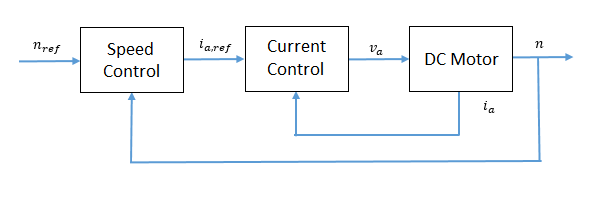
Чтобы удовлетворить необходимую производительность управления для простой дискретной модели объекта управления, Gf (z-1), используют систему управления PI замкнутого цикла GPI(z-1). Переходная производительность может быть выражена с точки зрения перерегулирования. Перерегулирование уменьшается относительно фактора затухания:
где,
σ является перерегулированием.
ξ фактор затухания.
Время отклика, tr, зависит от затухания и собственной частоты, ωn, такого что:
Если ξ <0.7,
Если ξ ≥ 0.7,
Общий рабочий процесс для разработки контроллера PI для системы первого порядка:
Дискретизируйте модель объекта управления с помощью метода дискретизации хранения нулевого порядка (ZOH). Таким образом, учитывая, что уравнение первого порядка, представляющее объект,
где,
Km является усилением первого порядка.
Tm является временной константой системы первого порядка.
Установка
приводит к дискретной модели объекта управления,
whereTs является шагом расчета для контроллера дискретного времени.
Запишите представление дискретного времени для контроллера PI, использующего то же преобразование. Для
установка
приводит к дискретным моделям контроллеров,
Объединение дискретных уравнений для объекта и контроллера приводит к передаточной функции замкнутого цикла для системы,
Знаменатель передаточной функции является характеристическим полиномом. Таким образом,
Характеристический полином для достижения необходимой производительности задан как
где,
Чтобы определить параметры контроллера, установите характеристический полином для системы, равной характеристическому полиному для необходимой производительности. Если
затем
и
Решение для q0 и урожаев q1
и
Поэтому общие уравнения для пропорциональных и интегральных параметров управления для системы первого порядка
и
Предположение, что для системы в модели в качестве примера Kb = Kt, упрощенные математические уравнения для напряжения и крутящего момента двигателя постоянного тока
и
где:
va является напряжением арматуры.
ia является текущей арматурой.
La является индуктивностью арматуры.
Ra является сопротивлением арматуры.
ω является ротором угловая скорость
Te является моторным крутящим моментом.
Tload является крутящим моментом загрузки.
Jm является моментом ротора инерции.
Bm является вязким коэффициентом трения.
Kb является коэффициентом пропорциональности.
Чтобы настроить текущий контроллер, примите, что модель линейна, то есть, что противоэлектродвижущая сила, как представлено Kbω, незначительна. Это предположение допускает приближение модели объекта управления с помощью этого уравнения Лапласа первого порядка:
Учитывая системные требования, можно теперь решить для KP и KI. Требования для текущего контроллера в модели в качестве примера:
Шаг расчета, Ts = 1 мс.
Промахнитесь, σ = 5%.
Время отклика, tr = 0,11 с.
Поэтому пропорциональные и интегральные параметры для текущего контроллера:
Чтобы настроить контроллер скорости, аппроксимируйте модель объекта управления с простой моделью. Сначала примите, что внутренний цикл намного быстрее, чем внешний цикл. Также примите, что нет никакой установившейся ошибки. Эти предположения допускают использование система первого порядка путем рассмотрения передаточной функции 1 для внутреннего текущего цикла.
Чтобы вывести вращательную скорость в оборотах в минуту, передаточная функция умножается на фактор 30/π. Чтобы взять в качестве управления вводит арматуру, текущую вместо моторного крутящего момента, передаточная функция умножается на коэффициент пропорциональности, Kb. Получившееся приближение для модели объекта управления внешнего цикла
У контроллера скорости есть тот же шаг расчета и требования перерегулирования как текущий контроллер, но время отклика медленнее, таково что:
Шаг расчета Ts = 1 мс.
Промахнитесь по σ = 5%.
Ответ time tr = 0,50 с.
Поэтому пропорциональные и интегральные параметры для контроллера скорости:
Исследуйте компоненты двигателя постоянного тока и каскадного контроллера.
Откройте модель. В командной строке MATLAB® войти
model = 'ee_dc_motor_control'
open_system(model)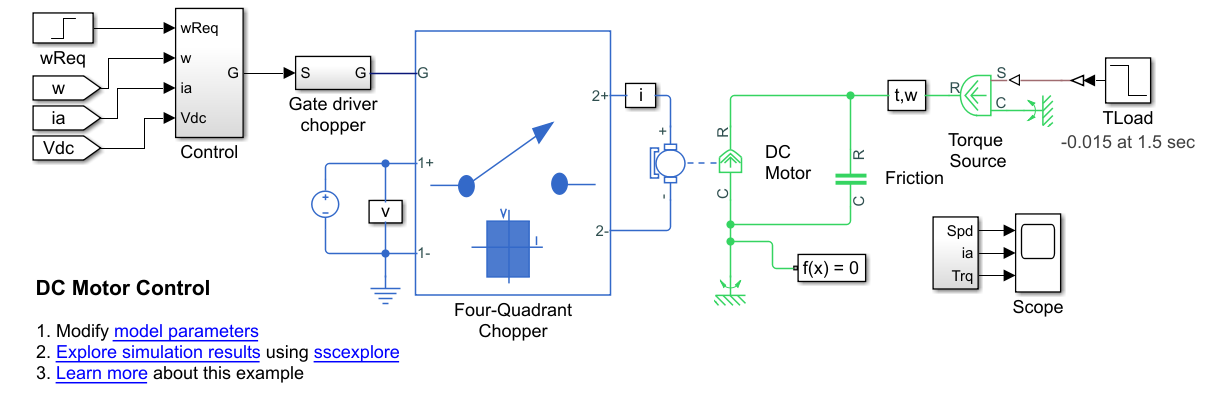
Подсистема Control содержит модель каскадной системы управления, созданной с помощью блоков от библиотеки Simulink®.
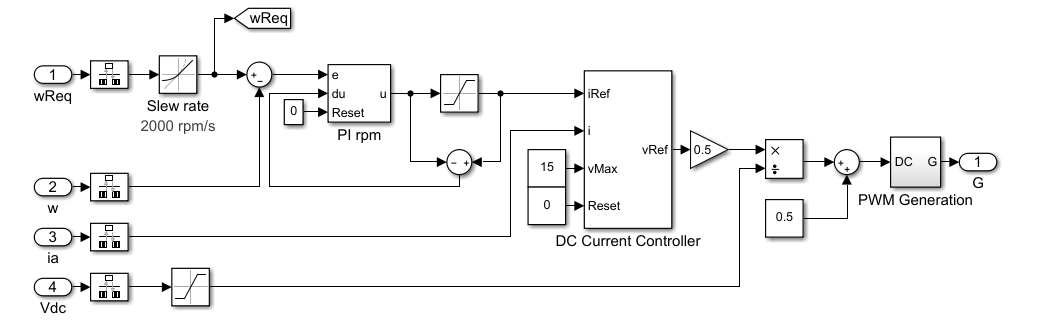
Блок Four Quadrant Chopper представляет прерыватель DC-DC с четырьмя квадрантами, который содержит два плеча мостовой схемы, каждое из которых имеет два IGBT (Идеал, Переключаясь) блоки. Когда входное напряжение превышает порог 0.5 V, IGBT (Идеал, Переключаясь), блоки ведут себя как линейные диоды с прямым напряжением 0.8 V и сопротивлением Ома 1e-4. Когда пороговое напряжение не превышено, IGBT (Идеал, Переключившись) действие блоков как линейные резисторы с проводимостью несостояния 1e-5 1/Ом.
Моделируйте модель.
sim(model)
Просмотрите результаты. Откройте блок Scope.
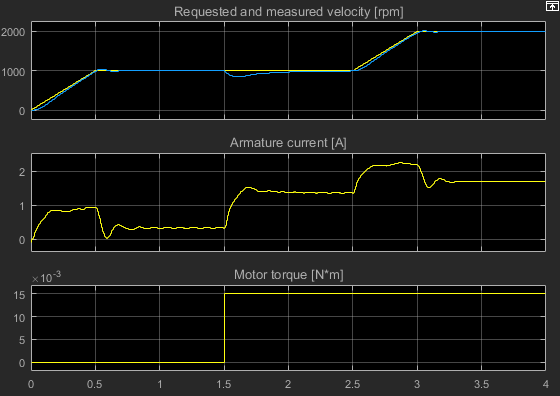
В 1,5 секунды существует крутящий момент загрузки, который приводит к установившейся ошибке.
Настройте контроллер двигателя постоянного тока. Функция ee_getDCMotorFirstOrderPIParams вычисляет пропорциональное усиление, KP, и интегральное усиление, KI, для системы первого порядка в этом примере.
Синтаксисом функций является [Kp, Ki] = getParamPI(Km,Tm,Ts,sigma,tr).
Входные параметры для функции являются системными параметрами и требованиями для контроллера:
Km является усилением первого порядка.
Tm является временной константой системы первого порядка.
Ts является шагом расчета для контроллера дискретного времени.
sigma является желаемым максимальным перерегулированием, σ.
tr является желаемым временем отклика.
Чтобы исследовать уравнения в функции, войти
edit ee_getDCMotorFirstOrderPIParamsЧтобы вычислить параметры контроллера с помощью функции, сохраните эти системные параметры в рабочую область:
Ra=4.67; % [Ohm] La=170e-3; % [H] Bm=47.3e-6; % [N*m/(rad/s)] Jm=42.6e-6; % [Kg*m^2] Kb=14.7e-3; % [V/(rad/s)] Tsc=1e-3; % [s]
Вычислите параметры для настройки текущего контроллера как функция параметров и требований для внутреннего контроллера:
Km = 1/Ra.
Tm = La/Ra.
Ts = Tsc.
sigma = 0.05.
Tr = 0.11.
[Kp_i, Ki_i] = ee_getDCMotorFirstOrderPIParams(1/Ra,La/Ra,Tsc,0.05,0.11)
Kp_i =
7.7099
Ki_i =
455.1491Параметры усиления для текущего контроллера сохранены в рабочую область.
Вычислите параметры для настройки контроллера скорости на основе параметров и требований для внешнего контроллера:
Km = Kb*(30/pi).
Tm = Jm/Ra.
Ts = Tsc.
sigma = 0.05.
Tr = 0.5.
[Kp_n, Ki_n] = ee_getDCMotorFirstOrderPIParams((Kb*(30/pi))/Bm,Jm/Bm,Tsc,0.05,0.5)
Kp_n =
0.0045
Ki_n =
0.0405Параметры усиления для контроллера скорости сохранены в рабочую область.
Моделируйте модель с помощью сохраненных параметров усиления для скорости и контроллеров.
sim(model)
Просмотрите результаты. Откройте блок Scope.
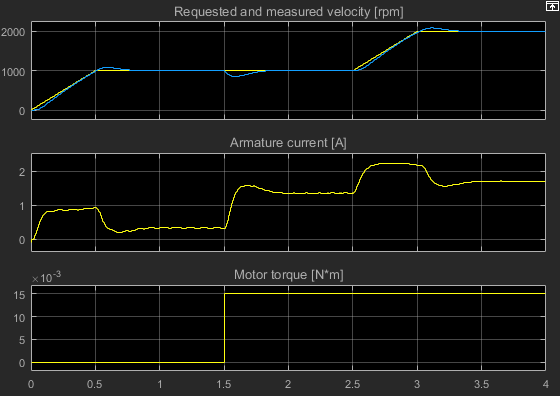
Существует немного больше перерегулирования, однако, контроллер намного быстрее отвечает на изменение крутящего момента загрузки.
Инерция | Вращательный электромеханический конвертер | Вращательное трение