Вычислите сингулярные значения Ганкеля для стабильной/нестабильной или непрерывной/дискретной системы
hankelsv(G) hankelsv(G,ErrorType,style) [sv_stab,sv_unstab]=hankelsv(G,ErrorType,style)
[sv_stab,sv_unstab]=hankelsv(G,ErrorType,style) возвращает вектор-столбец SV_STAB, содержащий сингулярные значения Ганкеля стабильной части G и SV_UNSTAB антистабильной части (если это существует). Ганкель СВ антистабильной части ss(a,b,c,d) вычисляется внутренне через ss(-a,-b,c,d). Дискретная модель преобразована в непрерывную через билинейное преобразование.
hankelsv(G) без выходных аргументов чертит гистограмму сингулярных значений Ганкеля, таких как следующее:
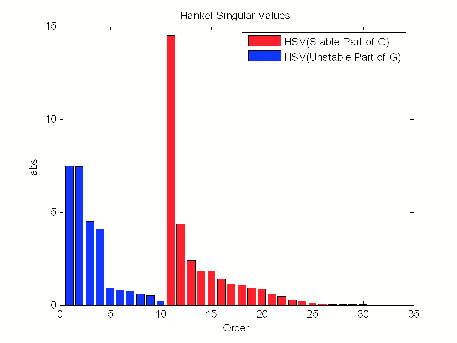
Эта таблица описывает дополнительные входные параметры для hankelsvd.
Аргумент | Значение | Описание |
|---|---|---|
ERRORTYPE |
| Постоянный Ганкель СВ G Ганкель СВ матрицы фазы Ганкель СВ взаимно-простых факторов |
STYLE |
| Абсолютное значение шкала логарифма |
IfErrorType = 'add', затем hankelsv реализует численно устойчивый метод квадратного корня, чтобы вычислить сингулярные значения Ганкеля [1]. Его алгоритм идет можно следующим образом:
Учитывая стабильную модель G, с управляемостью и наблюдаемостью grammians P и Q, вычисляют SVD P и Q:
[Up,Sp,Vp] = svd(P); [Uq,Sq,Vq] = svd(Q);
Затем сформируйте квадратные корни из grammians:
Lr = Up*diag(sqrt(diag(Sp))); Lo = Uq*diag(sqrt(diag(Sq)));
Сингулярные значения Ганкеля просто:
σ H =svd(Lo'*Lr);
Этот метод не только пользуется премуществами устойчивого алгоритма SVD, но также и гарантируйте, что вычисления остаются хорошо в “квадратном корне” из точности машины.
Если ErrorType = 'mult', то hankelsv вычисляет сингулярное значение Ганкеля матрицы фазы G [2].
Если ErrorType = 'ncf', то hankelsv вычисляет сингулярное значение Ганкеля нормированной взаимно-простой факторной пары модели [3].
[1] Сафонов, M.G., и Р.И. Чанг, “Метод Шура для Сбалансированного Снижения сложности модели”, Сделка IEEE на Автомате. Противоречие, издание AC-2, № 7, июль 1989, стр 729-733.
[2] Сафонов, M.G., и Р.И. Чанг, “Снижение сложности модели для Устойчивого Управления: Метод Относительной погрешности Шура”, Международный J. Адаптивного управления и Обработки сигналов, Издания 2, стр 259-272, 1988.
[3] Vidyasagar, M., синтез системы управления - подход факторизации. Лондон: нажатие MIT, 1985.