Rainflow значит анализ усталости
c = rainflow(x)c = rainflow(x,fs)c = rainflow(x,t)c = rainflow(xt)c = rainflow(___,'ext')[c,rm,rmr,rmm] = rainflow(___)[c,rm,rmr,rmm,idx] = rainflow(___)rainflow(___)rainflow(___) без выходных аргументов строит реверсирования загрузки и rainflow матричную гистограмму в текущей фигуре.
Анализ усталости учится, как повреждение накапливается в объекте, подвергнутом циклическим изменениям при напряжении. Количество циклов, необходимых, чтобы повредить объект, зависит от амплитуды цикла. Широкополосное входное возбуждение содержит циклы разнообразной амплитуды, и присутствие гистерезиса в объекте имеет эффект вложения некоторые циклы в других, или полностью или частично. Rainflow рассчитывая оценивает количество циклов изменения загрузки как функция амплитуды цикла.
Первоначально, rainflow превращает историю загрузки в последовательность реверсирований. Реверсирования являются локальными минимумами и максимумами, где загрузка изменяет знак. Функциональные циклы количеств путем рассматривания движущегося контрольного вопроса последовательности, Z, и перемещения заказали подмножество с тремя точками с этими характеристиками:
Первые и вторые точки коллективно называются Y.
Вторые и третьи точки коллективно называются X.
В обоих X и Y точки сортируются от ранее до позже вовремя, но не обязательно последовательны в последовательности реверсирования.
Область значений X, обозначенный r (X), является абсолютным значением различия между амплитудой первой точки и амплитудой второй точки. Определение r (Y) аналогично.
Алгоритм rainflow следующие:
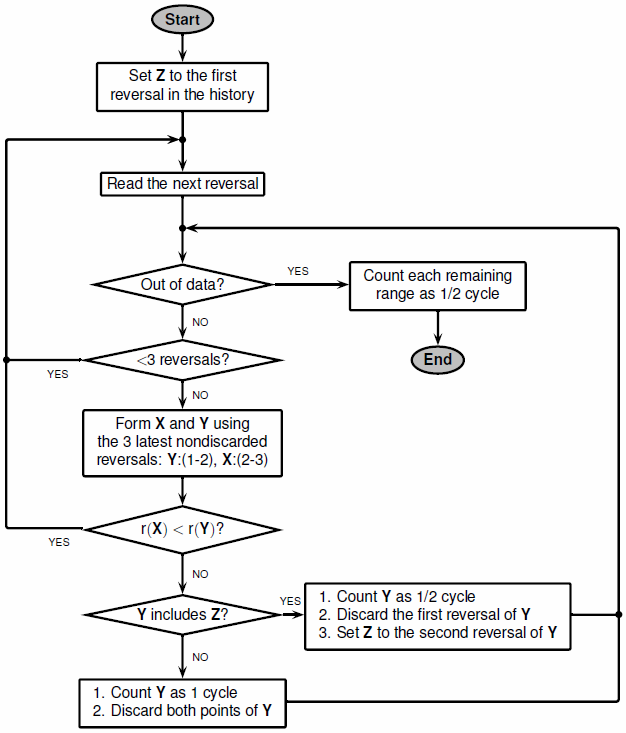
В конце функция собирает различные циклы и полупериоды и сводит в таблицу их области значений, их средние значения и точки, в которых они запускают и заканчиваются. Эта информация может затем использоваться, чтобы произвести гистограмму циклов.
Рассмотрите следующую последовательность реверсирования:
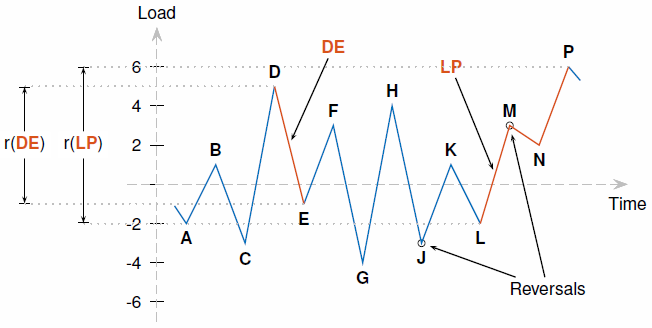
| Шаг | Z | Реверсирования | Три реверсирования? | Y | r (Y) | X | r (X) | r (X) <r (Y)? | Z в Y? | Действия |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | A, B, C | Да | A, B | 3 | До н.э | 4 | Нет | Да |
|
| 2 | B | B, C | Нет | — | — | — | — | — | — | Рид Д. |
| 3 | B | B, C, D | Да | До н.э | 4 | CD | 8 | Нет | Да |
|
| 4 | C | CD | Нет | — | — | — | — | — | — | Рид Э. |
| 5 | C | C, D, E | Да | CD | 8 | DE | 6 | Да | — | Рид Ф. |
| 6 | C | C, D, E, F | Да | DE | 6 | EF | 4 | Да | — | Рид Г. |
| 7 | C | C, D, E, F, G | Да | EF | 4 | FG | 7 | Нет | Нет |
|
| 8 | C | C, D, G | Да | CD | 8 | DG | 9 | Нет | Да |
|
| 9 | D | D, G | Нет | — | — | — | — | — | — | Рид Х. |
| 10 | D | D, G, H | Да | DG | 9 | GH | 8 | Да | — | Рид Дж. |
| 11 | D | D, G, H, J | Да | GH | 8 | HJ | 7 | Да | — | Рид К. |
| 12 | D | D, G, H, J, K | Да | HJ | 7 | JK | 4 | Да | — | Рид Л. |
| 13 | D | D, G, H, J, K, L | Да | JK | 4 | KL | 3 | Да | — | Рид М. |
| 14 | D | D, G, H, J, K, L, M | Да | KL | 3 | LM | 5 | Нет | Нет |
|
| 15 | D | D, G, H, J, M | Да | HJ | 7 | JM | 5 | Да | — | Рид Н. |
| 16 | D | D, G, H, J, M, N | Да | JM | 5 | M, n | 1 | Да | — | Рид П. |
| 17 | D | D, G, H, J, M, N, P | Да | M, n | 1 | NP | 4 | Нет | Нет |
|
| 18 | D | D, G, H, J, P | Да | HJ | 7 | МИРОВОЙ СУДЬЯ | 9 | Нет | Нет |
|
| 19 | D | D, G, P | Да | DG | 9 | GP | 10 | Нет | Да |
|
| 20 | G | G, P | Из данных | — | — | — | — | — | — |
Считайте GP как ½ цикла. |
Теперь соберите результаты.
| Количество цикла | Область значений | Среднее значение | Запуск | Конец |
|---|---|---|---|---|
| ½ | 3 | –0.5 | A | B |
| ½ | 4 | –1 | B | C |
| 1 | 4 | 1 | E | F |
| ½ | 8 | 1 | C | D |
| 1 | 3 | –0.5 | K | L |
| 1 | 1 | 2.5 | M | N |
| 1 | 7 | 0.5 | H | J |
| ½ | 9 | 0.5 | D | G |
| ½ | 10 | 1 | G | P |
Сравните это с результатом выполнения rainflow на последовательности:
q = rainflow([-2 1 -3 5 -1 3 -4 4 -3 1 -2 3 2 6])
q =
0.5000 3.0000 -0.5000 1.0000 2.0000
0.5000 4.0000 -1.0000 2.0000 3.0000
1.0000 4.0000 1.0000 5.0000 6.0000
0.5000 8.0000 1.0000 3.0000 4.0000
1.0000 3.0000 -0.5000 10.0000 11.0000
1.0000 1.0000 2.5000 12.0000 13.0000
1.0000 7.0000 0.5000 8.0000 9.0000
0.5000 9.0000 0.5000 4.0000 7.0000
0.5000 10.0000 1.0000 7.0000 14.0000[1] ASTM E1049-85 (2017), "Общепринятая практика для цикла, рассчитывающего в анализе усталости". Уэст-Коншохокен, PA: международный ASTM, 2011, https://www.astm.org/cgi-bin/resolver.cgi?E1049.