Системные модели дискретного времени

Системные модели дискретного времени являются представительными схемами цифровых фильтров. Техническая вычислительная среда MATLAB^® поддерживает несколько системных моделей дискретного времени, которые описаны в следующих разделах:

Передаточная функция

Передаточная функция является основным представлением z-области цифрового фильтра, выражая фильтр как отношение двух полиномов. Это - основная модель дискретного времени для этого тулбокса. Описание модели передаточной функции для z-преобразования разностного уравнения цифрового фильтра

$Y (z) = \frac{b (1) + b (2) z^{- 1} + \dots + b (n + 1) z^{- n}}{a (1) + a (2) z^{- 1} + \dots + a (m + 1) z^{- m}} X (z)$

Здесь, константы, b (i) и a (i) является коэффициентами фильтра и порядком фильтра, являются максимумом n и m. В среде MATLAB вы храните эти коэффициенты в двух векторах (векторы - строки условно), один вектор - строка для числителя и один для знаменателя. Дополнительную информацию см. в Фильтрах и Передаточных функциях на форме передаточной функции.

Нули и полюса

Форма учтенного или нулей и полюсов передаточной функции

$H (z) = \frac{q (z)}{p (z)} = k \frac{(z - q (1)) (z - q (2)) ... (z - q (n))}{(z - p (1)) (z - p (2)) ... (z - p (n))}$

Условно, полиномиальные коэффициенты хранятся в векторах - строках и полиномиальных корнях в вектор-столбцах. В форме нулей и полюсов, поэтому, нуль и местоположения полюса для числителя и знаменателя передаточной функции находятся в вектор-столбцах. Учтенное усиление передаточной функции k является скаляром MATLAB.

poly и функции roots преобразовывают между представлениями нулей и полюсов и полиномом. Например, простой БИХ-фильтр

b = [2 3 4];
a = [1 3 3 1];

Нули и полюса этого фильтра

q = roots(b)
p = roots(a)
% Gain factor
k = b(1)/a(1)

Возврат исходным полиномам,

bb = k*poly(q)
aa = poly(p)

Обратите внимание на то, что b и a в этом случае представляют передаточную функцию:

$H (z) = \frac{2 + 3 z^{- 1} + 4 z^{- 2}}{1 + 3 z^{- 1} + 3 z^{- 2} + z^{- 3}} = \frac{2 z^{2} + 3 z + 4}{z^{3} + 3 z^{2} + 3 z + 1}$

Для b = [2 3 4], функция roots пропускает нуль для z, равного 0. На самом деле это пропускает полюса и нули для z, равного 0 каждый раз, когда входная передаточная функция имеет больше полюсов, чем нули, или наоборот. Это приемлемо в большинстве случаев. Чтобы обойти проблему, однако, просто добавляют нули, чтобы сделать векторы той же длиной перед использованием функции roots; например, b = [b 0].

Пространство состояний

Всегда возможно представлять цифровой фильтр или систему разностных уравнений, как набор разностных уравнений первого порядка. В форме матричного или пространства состояний можно записать уравнения как

$\begin{matrix} x (n + 1) = A x (n) + B u (n) \\ y (n) = C x (n) + D u (n) \end{matrix}$

где u является входом, x является вектором состояния, и y является вывод. Для одноканальных систем A является m-by-m матрица, где m является порядком фильтра, B является вектор-столбцом, C является вектором - строкой, и D является скаляром. Обозначение пространства состояний особенно удобно для многоканальных систем, где вход u и вывод y становятся векторами, и B, C, и D становится матрицами.

Представление пространства состояний расширяет легко к среде MATLAB. A, B, C и D являются прямоугольными массивами; функции MATLAB обрабатывают их как отдельные переменные.

Взятие Z-преобразования уравнений пространства состояний и объединение их показывают эквивалентность форм передаточной функции и пространства состояний:

$Y (z) = H (z) U (z), где H (z) = C {(z I - A)}^{- 1} B + D$

Не будьте заинтересованы, не ли вы знакомы с представлением пространства состояний линейных систем. Некоторые алгоритмы проекта фильтра используют форму пространства состояний внутренне, но не требуют, чтобы любое знание концепций пространства состояний использовало их успешно. Если ваши приложения используют основанную на пространстве состояний обработку сигналов экстенсивно, однако, смотрите продукт Control System Toolbox™ для всесторонней библиотеки инструментов пространства состояний.

Расширение элементарной дроби (форма остатка)

Каждая передаточная функция также имеет соответствующее расширение элементарной дроби или представление формы остатка, данное

$\frac{b (z)}{a (z)} = \frac{r (1)}{1 - p (1) z^{- 1}} + ... + \frac{r (n)}{1 - p (n) z^{- 1}} + k (1) + k (2) z^{- 1} + ... + k (m - n + 1) z^{- (m - n)}$

если H (z) не имеет никаких повторных полюсов. Здесь, n является степенью полинома знаменателя рациональной передаточной функции b (z)/a (z). Если r является полюсом кратности _sr, то H (z) имеет условия формы:

$\frac{r (j)}{1 - p (j) z^{- 1}} + \frac{r (j + 1)}{{(1 - p (j) z^{- 1})}^{2}} ... + \frac{r (j + s_{r} - 1)}{{(1 - p (j) z^{- 1})}^{s_{r}}}$

residuez Signal Processing Toolbox™ функционирует в передаточных функциях преобразований к и от формы расширения элементарной дроби. “z” на конце residuez обозначает z-область или дискретную область. residuez возвращает полюса в вектор-столбце p, остатки, соответствующие полюсам в вектор-столбце r и любая неподходящая часть исходной передаточной функции подряд векторный k. residuez решает, что два полюса являются тем же самым, если значение их различия меньше, чем 0,1 процента любого из значений полюсов.

Расширение элементарной дроби возникает в обработке сигналов как один метод нахождения обратного Z-преобразования передаточной функции. Например, расширение элементарной дроби

$H (z) = \frac{- 4 + 8 z^{- 1}}{1 + 6 z^{- 1} + 8 z^{- 2}}$

b = [-4 8];
a = [1 6 8];
[r,p,k] = residuez(b,a)

который соответствует

$H (z) = \frac{- 12}{1 + 4 z^{- 1}} + \frac{8}{1 + 2 z^{- 1}}$

Чтобы найти обратное Z-преобразование H (z), найдите сумму обратных Z-преобразований двух слагаемых H (z), дав причинный импульсный ответ:

$h (n) = - 12 {(- 4)}^{n} + 8 {(- 2)}^{n}, n = 0, 1, 2, \dots$

Чтобы проверить это в среде MATLAB, ввести

imp = [1 0 0 0 0];
resptf = filter(b,a,imp)
respres = filter(r(1),[1 -p(1)],imp)+...
  filter(r(2),[1 -p(2)],imp)

Разделы второго порядка (SOS)

Любая передаточная функция H (z) имеет представление разделов второго порядка

$H (z) = \prod_{k = 1}^{L} H_{k} (z) = \prod_{k = 1}^{L} \frac{b_{0 k} + b_{1 k} z^{- 1} + b_{2 k} z^{- 2}}{a_{0 k} + a_{1 k} z^{- 1} + a_{2 k} z^{- 2}}$

где L является количеством разделов второго порядка, которые описывают систему. Среда MATLAB представляет форму раздела второго порядка системы дискретного времени как L-by-6 массив sos. Каждая строка sos содержит один раздел второго порядка, где элементы строки являются тремя числителями и тремя коэффициентами знаменателя, которые описывают раздел второго порядка.

$SOS = (\begin{array}{l} b_{01} & b_{11} & b_{21} & a_{01} & a_{11} & a_{21} \\ b_{02} & b_{12} & b_{22} & a_{02} & a_{12} & a_{22} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ b_{0 L} & b_{1 L} & b_{2 L} & a_{0 L} & a_{1 L} & a_{2 L} \end{array})$

Существует много способов представлять фильтр в форме раздела второго порядка. Посредством тщательного соединения полюса и нулевых пар, упорядоченного расположения разделов в каскаде и мультипликативного масштабирования разделов, возможно уменьшать усиление шума квантования и избежать переполнения в некоторых реализациях фильтра фиксированной точки. Функции zp2sos и ss2sos, описанный в Преобразованиях Линейной системы, выполняют нулевое полюсом соединение, масштабирование раздела и упорядоченное расположение раздела.

Примечание

Весь Signal Processing Toolbox преобразования раздела второго порядка применяется только к цифровым фильтрам.

Структура решетки

Для дискретного все-полюса N-го порядка или все-нулевого фильтра, описанного полиномиальными коэффициентами (n), n = 1, 2 ..., N+1, существуют соответствующие коэффициенты структуры решетки N k (n), n = 1, 2 ..., N. Параметры k (n) также называются отражательными коэффициентами фильтра. Учитывая эти отражательные коэффициенты, можно реализовать дискретный фильтр как показано ниже.

КИХ и БИХ-схемы структуры Фильтра Решетки

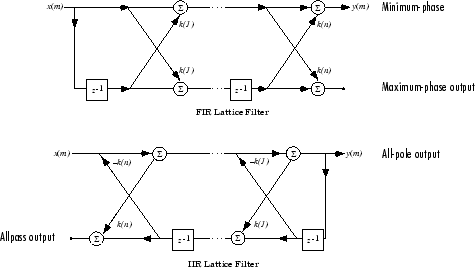
Для общего нулевого полюсом БИХ-фильтра, описанного полиномиальными коэффициентами a и b, существует и коэффициенты решетки k (n) для знаменателя a и лестничные коэффициенты v (n) для числителя b. Фильтр решетки/лестничной структуры может быть реализован как

Схема фильтра решетки/лестничной структуры

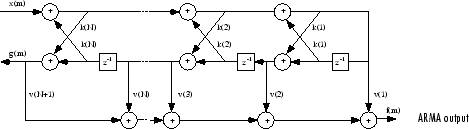
Функция тулбокса tf2latc принимает КИХ или БИХ, просачивается, полином формируется, и возвращает соответствующие отражательные коэффициенты. КИХ в качестве примера просачивается, полиномиальная форма

b = [1.0000   0.6149   0.9899   0.0000   0.0031  -0.0082];

Решетка этого фильтра (отражательный коэффициент) представление

k = tf2latc(b)

Для БИХ-фильтров значение отражательных коэффициентов обеспечивает легкую проверку устойчивости. Если все отражательные коэффициенты, соответствующие полиному, имеют значение меньше чем 1, все корни того полинома в модульном кругу. Например, считайте БИХ-фильтр с полиномом числителя b сверху и полиномом знаменателя:

a = [1 1/2 1/3];

Представление решетки фильтра

[k,v] = tf2latc(b,a);

Поскольку abs(k) < 1 для всех отражательных коэффициентов в k, фильтр стабилен.

Функциональный latc2tf вычисляет полиномиальные коэффициенты для фильтра от его решетки (отражение) коэффициенты. Учитывая отражательный вектор коэффициентов k, соответствующая полиномиальная форма

b = latc2tf(k);

Коэффициенты решетки или решетки/лестничной структуры могут использоваться, чтобы реализовать фильтр с помощью функционального latcfilt.

Матрица свертки

В обработке сигналов, применяя операцию свертки к двум векторам или матрицам эквивалентно фильтрации одного из входных операндов другим. Это отношение разрешает представление цифрового фильтра как матрица свертки.

Учитывая любой вектор, функция тулбокса convmtx генерирует матрицу, скалярное произведение которой с другим вектором эквивалентно свертке этих двух векторов. Сгенерированная матрица представляет цифровой фильтр, что можно обратиться к любому вектору соответствующей длины; внутренняя размерность операндов должна согласиться вычислить скалярное произведение.

Матрица свертки для векторного b, представляя коэффициенты числителя для цифрового фильтра,

b = [1 2 3];
x = randn(3,1);
C = convmtx(b',3);

Два эквивалентных способа применить операцию свертки к b с x следующие.

y1 = C*x;
y2 = conv(b,x);

Документация