Чтобы моделировать динамическую систему, вы вычисляете ее состояния на последовательных временных шагах по промежутку требуемого времени. Это вычисление использует информацию, предоставленную моделью системы. Time steps является временными интервалами, когда вычисление происходит. Размер этого временного интервала называется step size. Процесс вычисления состояний модели этим способом известен как solving модель. Никакой отдельный метод решения модели не применяется ко всем системам. Simulink® обеспечивает набор программ под названием solvers. Каждый решатель воплощает конкретный подход к решению модели.
Решатель применяет численный метод решить набор обыкновенных дифференциальных уравнений, которые представляют модель. Посредством этого вычисления это определяет время следующего шага симуляции. В процессе решения этой задачи с начальными значениями решатель также удовлетворяет требования точности, чтобы вы задали.
Simulink обеспечивает два основных типа решателей — решатели переменного шага и фиксированный шаг. Вы видите решатели под каждым типом в панели Solver образцовых параметров конфигурации.
Решатели широко классифицируются с помощью этих критериев:
Тип размера шага используется в вычислении
Решатели фиксированного шага, как имя предполагает, решают модель в фиксированных размерах шага с начала в конец симуляции. Можно задать размер шага или позволить решателю выбрать его. Обычно уменьшение размера шага увеличивает точность результатов и увеличивает время, требуемое моделировать систему.
Решатели переменного шага отличаются размер шага во время симуляции. Они уменьшают размер шага, чтобы увеличить точность когда состояния образцового изменения быстро и во время событий пересечения нулем. Они увеличивают размер шага, чтобы не делать ненужные шаги когда состояния образцового изменения медленно. Вычисление размера шага добавляет к вычислительным издержкам на каждом шаге. Однако это может сократить общее количество шагов, и следовательно время симуляции, требуемое поддержать заданный уровень точности для моделей с кусочно-непрерывными или быстро изменяющимися состояниями.
Природа состояний в модели
Непрерывные решатели используют численное интегрирование, чтобы вычислить непрерывные состояния модели на шаге текущего времени на основе состояний на предыдущих временных шагах и производных состояния. Непрерывные решатели полагаются на отдельные блоки, чтобы вычислить значения дискретных состояний модели на каждом временном шаге.
Дискретные решатели, в основном, для решения чисто дискретных моделей. Они вычисляют только следующий шаг времени симуляции для модели. Когда они выполняют это вычисление, они полагаются на каждый блок в модели, чтобы обновить ее отдельное дискретное состояние. Они не вычисляют непрерывные состояния.
При выборе решателя для симуляции модели рассмотрите:
Динамика системы
Устойчивость решения
Скорость вычисления
Робастность решателя
Решатель не может полностью удовлетворить все ваши требования, так используйте итерационный подход при выборе один. Сравните результаты симуляции от нескольких решателей и выберите тот, который предлагает лучшую производительность с минимальными компромиссами.
Существует два способа выбрать решатель для вашей модели:
Используйте автоматический решатель. Новым моделям установили их выбор решателя на автоматический решатель по умолчанию. Автоматический решатель рекомендует фиксированный шаг или решатель переменного шага для вашего образцового, а также максимального размера шага. Для получения дополнительной информации смотрите Использование Автоматический Решатель, чтобы Выбрать Solver
Если вы не удовлетворены результатами симуляции с помощью автоматического решателя, выберите решатель в панели Solver в образцовых параметрах конфигурации.
Когда вы создаете и моделируете модель, можно выбрать решатель на основе динамики модели. Решатель переменного шага лучше подходит для чисто непрерывных моделей, как динамика массовой пружинной системы демпфера. Решатель фиксированного шага рекомендуется для модели, которая содержит несколько переключателей, как энергосистема инвертора, из-за количества сброса решателя, который заставил бы решатель переменного шага вести себя как решатель фиксированного шага.
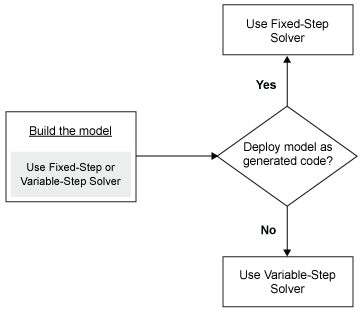
Когда вы развертываете модель как сгенерированный код, можно использовать только решатель фиксированного шага. Если вы выбираете решатель переменного шага во время симуляции, используйте ее, чтобы вычислить размер шага, требуемый для решателя фиксированного шага, в котором вы нуждаетесь при развертывании.
Этот график обеспечивает широкую классификацию решателей в Библиотеке Simulink.
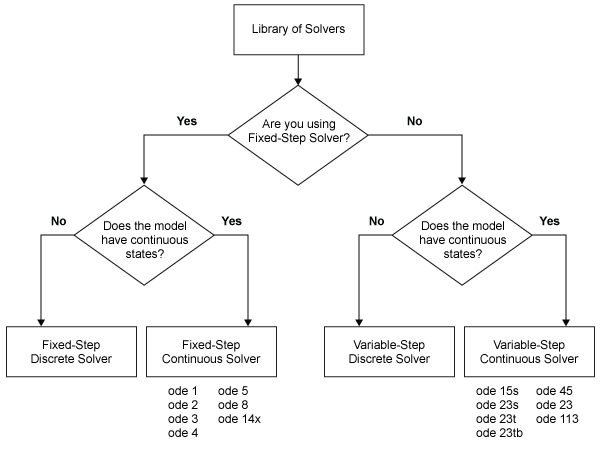
Чтобы адаптировать выбранный решатель в соответствии с вашей моделью, смотрите Проверку и Улучшите Точность Симуляции.
Идеально, решатель, который вы выбираете, должен:
Решите модель успешно.
Для решателей переменного шага предоставьте решение в пределах допуска, которые вы задаете.
Решите модель в разумной длительности.
Один решатель не может удовлетворить все эти требования. Попытайтесь моделировать с несколькими решателями прежде, чем сделать выбор.
Библиотека Simulink обеспечивает несколько решателей, все из которых могут работать с алгебраическим решателем цикла. Для получения дополнительной информации смотрите Как Алгебраические работы Решателя Цикла.
| Дискретный | Непрерывный | Переменный порядок | ||
|---|---|---|---|---|
| Фиксированный шаг | Явный | Не применяется | Фиксированный шаг непрерывные явные решатели | Не применяется |
| Неявный | Не применяется | Фиксированный шаг непрерывные неявные решатели | Не применяется | |
| Переменный шаг | Явный | Выберите решатель Переменного Шага | Переменный шаг непрерывные явные решатели | Одноразрядный по сравнению с переменным порядком непрерывные решатели |
| Неявный | Переменный шаг непрерывные неявные решатели | Одноразрядный по сравнению с переменным порядком непрерывные решатели |
В панели Solver образцовых параметров конфигурации Библиотека Simulink решателей разделена на два главных типа. Смотрите Фиксированный Шаг По сравнению с Решателями Переменного Шага.
Можно далее категоризировать решатели каждого типа:
Дискретный по сравнению с непрерывными решателями
Явный по сравнению с неявными непрерывными решателями
Один шаг по сравнению с многоступенчатыми непрерывными решателями
Один порядок по сравнению с переменным порядком непрерывные решатели
Фиксированный шаг и решатели переменного шага вычисляют следующее время симуляции как сумму текущего времени симуляции и размера шага. Управление Type на панели настройки Solver позволяет вам выбирать тип решателя. С решателем фиксированного шага размер шага остается постоянным в течение симуляции. С решателем переменного шага размер шага может отличаться от шага до шага, в зависимости от образцовой динамики. В частности, решатель переменного шага увеличивает или уменьшает размер шага, чтобы соответствовать ошибочным допускам, которые вы задаете.
Выбор между этими типами зависит от того, как вы планируете развернуть свою модель и образцовую динамику. Если вы планируете сгенерировать код из своей модели и запустить код по компьютерной системе в реальном времени, выбрать решатель фиксированного шага, чтобы моделировать модель. Вы не можете сопоставить размер переменного шага с часами реального времени.
Если вы не планируете развернуть свою модель как сгенерированный код, выбор между переменным шагом и решателем фиксированного шага зависит от динамики вашей модели. Решатель переменного шага может сократить время симуляции вашей модели значительно. Решатель переменного шага позволяет это сохранение, потому что для данного уровня точности решатель может динамически настроить размер шага по мере необходимости. Этот подход сокращает количество требуемых шагов. Решатель фиксированного шага должен использовать один размер шага в течение симуляции, на основе требований точности. Чтобы удовлетворить эти требования в течение симуляции, решатель фиксированного шага обычно требует небольшого шага.
ex_multirate показывает, как решатель переменного шага может сократить время симуляции для многоскоростной дискретной модели.
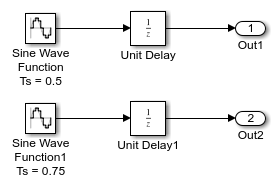
Модель генерирует выходные параметры на двух различных уровнях: каждые 0,5 с и каждые 0,75 с. Чтобы получить оба выходных параметров, решатель фиксированного шага должен взять временной шаг каждые 0,25 с (основной шаг расчета для модели).
[0.0 0.25 0.5 0.75 1.0 1.25 1.5 ...]
В отличие от этого, решатель переменного шага должен предпринять шаги только, когда модель генерирует вывод.
[0.0 0.5 0.75 1.0 1.5 ...]
Эта схема значительно сокращает количество временных шагов, требуемых моделировать модель.
Когда вы выбираете тип решателя, можно также выбрать определенный решатель. Оба набора решателей включают два типа: дискретный и непрерывный. Дискретные и непрерывные решатели полагаются на блоки модели, чтобы вычислить значения любых дискретных состояний. Блоки, которые задают дискретные состояния, ответственны за вычисление значений тех состояний на каждом временном шаге. Однако различающиеся дискретные решатели, непрерывные решатели используют численное интегрирование, чтобы вычислить непрерывные состояния, которые задают блоки. При выборе решателя определите сначала, использовать ли дискретный решатель или непрерывный решатель.
Если ваша модель не имеет никаких непрерывных состояний, то Simulink переключается или на фиксированный шаг дискретный решатель или на переменный шаг дискретный решатель. Если ваша модель имеет только непрерывные состояния или соединение непрерывных и дискретных состояний, выберите непрерывный решатель из остающегося выбора решателя на основе динамики вашей модели. В противном случае ошибка происходит.
Библиотека решателя содержит два дискретных решателя — фиксированный шаг дискретный решатель и переменный шаг дискретный решатель. Решатель фиксированного шага по умолчанию выбирает размер шага и уровень симуляции достаточно быстро, чтобы отследить изменения состояния в самом быстром блоке в вашей модели. Решатель переменного шага настраивает размер шага симуляции, чтобы идти в ногу с фактическим уровнем изменений дискретного состояния в вашей модели. Эта корректировка может избежать ненужных шагов и сократить время симуляции для многоскоростных моделей (см. Шаги расчета в Системах для получения дополнительной информации.)
Фиксированный шаг дискретные решатели не решает для дискретных состояний. Каждый блок вычисляет свои дискретные состояния независимо от решателя.
Вы представляете явную систему системой уравнения
Для любого данного значения x можно вычислить путем замены x в f(x) и оценки уравнения.
Уравнения формы
считаются неявными. Для любого данного значения , необходимо решить это уравнение, чтобы вычислить .
Линейно неявная система может быть представлена уравнением
M (x) называется большой матрицей и функция принуждения. Система становится линейно неявной, когда вы используете физические блоки моделирования в модели.
В то время как можно применить неявный или явный непрерывный решатель, чтобы решить все эти системы, неявные решатели специально разработаны для решения жестких проблем. Явные решатели решают нежесткие проблемы. Проблема обыкновенного дифференциального уравнения, как говорят, жестка, если требуемое решение медленно отличается, но существуют более близкие решения, которые отличаются быстро. Численный метод должен затем взять маленькие временные шаги, чтобы решить систему. Жесткость является проблемой эффективности. Чем более жесткий система, тем дольше она берет к для явного решателя, чтобы выполнить вычисление. Жесткая система имеет и медленно и быстро переменная непрерывная динамика.
Когда по сравнению с явными решателями, неявные решатели обеспечивают большую устойчивость для колебательного поведения. Однако неявные решатели являются также в вычислительном отношении более дорогими. Они генерируют якобиевскую матрицу и решают набор алгебраических уравнений на каждом временном шаге с помощью подобного Ньютону метода. Чтобы уменьшать эти дополнительные расходы, неявные решатели предлагают параметр Solver Jacobian method, который позволяет вам улучшать производительность симуляции неявных решателей. Смотрите Выбирают Jacobian Method для Неявного Решателя для получения дополнительной информации. Неявные решатели более эффективны, чем явные решатели для решения линейно неявной системы.
Библиотека решателя Simulink обеспечивает и и многоступенчатые решатели с одним шагом. Оценка решателей с одним шагом![]() с помощью решения в непосредственно предшествующем моменте времени
с помощью решения в непосредственно предшествующем моменте времени ![]() и значений производной в нескольких точках между tn и tn-1. Эти точки являются незначительными шагами.
и значений производной в нескольких точках между tn и tn-1. Эти точки являются незначительными шагами.
Многоступенчатые решатели используют результаты на нескольких предыдущих временных шагах, чтобы вычислить текущее решение. Simulink обеспечивает один явный многоступенчатый решатель, ode113, и один неявный многоступенчатый решатель, ode15s. Оба - решатели переменного шага.
Это различие основано на количестве порядков что использование решателя, чтобы решить систему уравнения. Два решателя переменного порядка, ode15s и ode113, являются частью библиотеки решателя. Они используют несколько порядков решить систему уравнений. А именно, неявный, переменный шаг, решатель ode15s использует первый порядок посредством уравнений пятого порядка, в то время как явный, переменный шаг решатель ode113 использует первый порядок посредством уравнений тринадцатого порядка. Для ode15s можно ограничить самый высокий порядок, примененный через параметр Maximum Order. Для получения дополнительной информации смотрите Максимальный Порядок.
Фиксированный шаг дискретный решатель вычисляет время следующего шага симуляции путем добавления фиксированного размера шага в текущее время. Точность и отрезок времени получившейся симуляции зависит от размера шагов, сделанных симуляцией: чем меньший размер шага, тем более точны результаты всего лишь дольше, симуляция берет. По умолчанию Simulink выбирает размер шага, или можно выбрать размер шага сами. Если вы выбираете настройку по умолчанию auto, и если модель имеет дискретные шаги расчета, то Simulink устанавливает размер шага на основной шаг расчета модели. В противном случае, если никакие дискретные уровни не существуют, наборы Simulink, размер к результату деления различия между симуляцией запускается и времена остановки 50.
При попытке использовать фиксированный шаг дискретный решатель, чтобы обновить или моделировать модель, которая имеет непрерывные состояния, сообщение об ошибке появляется. Таким образом выбор решателя фиксированного шага и затем обновление или симуляция модели являются быстрым способом определить, имеет ли модель непрерывные состояния.
Фиксированный шаг непрерывные решатели, как фиксированный шаг дискретный решатель, вычисляет следующее время симуляции путем добавления временного шага фиксированного размера в текущее время. Для каждого из этих шагов непрерывные решатели используют численное интегрирование, чтобы вычислить значения непрерывных состояний для модели. Эти значения вычисляются с помощью непрерывных состояний на предыдущем временном шаге и производных состояния в промежуточных точках (незначительные шаги) между током и предыдущим временным шагом.
Simulink использует фиксированный шаг дискретный решатель для модели, которая не содержит состояний или только дискретных состояний, даже если вы задаете фиксированный шаг непрерывный решатель для модели.
Simulink обеспечивает два типа фиксированного шага непрерывные решатели — явный и неявный.
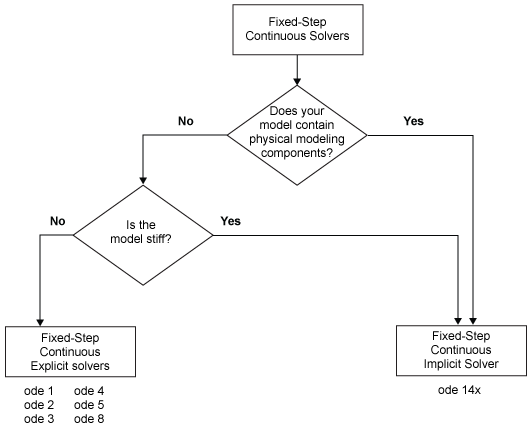
Различие между этими двумя типами заключается в скорости и устойчивости. Неявный решатель требует большего количества вычисления на шаг, чем явный решатель, но более стабилен. Поэтому неявный решатель фиксированного шага, который обеспечивает Simulink, более владеет мастерством решения жесткой системы, чем фиксированный шаг явные решатели. Для получения дополнительной информации смотрите Явный По сравнению с Неявными Непрерывными Решателями.
Фиксированный шаг Непрерывные Явные Решатели. Явные решатели вычисляют значение состояния на следующем временном шаге как явная функция текущих значений и состояния и производной состояния. Фиксированный шаг явный решатель выражается математически как:
где x является состоянием, Dx является зависимой решателем функцией, которая оценивает производную состояния, h является размером шага, и n указывает на шаг текущего времени.
Simulink обеспечивает набор фиксированного шага непрерывные явные решатели. Решатели отличаются по определенному методу численного интегрирования, который они используют, чтобы вычислить производные состояния модели. Эта таблица приводит каждый решатель и метод интегрирования, который это использует. Таблица приводит решатели в порядке вычислительной сложности методов интегрирования, которые они используют от наименее комплексного (ode1) к самому комплексному (ode8).
| Решатель | Метод интегрирования | Порядок точности |
|---|---|---|
| Метод Эйлера | Сначала |
| Метод Хеуна | Второй |
| Формула Шемпина Богацков | Треть |
| Четвертый порядок формула (RK4) Рунге-Кутта | Четвертый |
| Dormand-принц (RK5) формула | Пятый |
| Формула Dormand-принца RK8 (7) | Восьмой |
Ни один из этих решателей не имеет механизм контроля ошибок. Поэтому точность и длительность симуляции зависят непосредственно от размера шагов, сделанных решателем. Когда вы уменьшаете размер шага, результаты становятся более точными, но симуляция занимает больше времени. Кроме того, для любого данного размера шага, чем выше порядок решателя, тем более точный результаты симуляции.
Если вы задаете тип решателя фиксированного шага для модели, то по умолчанию, Simulink выбирает решатель FixedStepAuto. Автоматический решатель затем выбирает соответствующий решатель фиксированного шага, который может обработать и непрерывные и дискретные состояния с умеренным вычислительным усилием. Как с дискретным решателем, если модель имеет дискретные уровни (шаги расчета), то Simulink устанавливает размер шага на основной шаг расчета модели по умолчанию. Если модель не имеет никаких дискретных уровней, Simulink автоматически использует результат деления общей длительности симуляции 50. Следовательно, решатель предпринимает шаги в каждом времени симуляции, в котором Simulink должен обновить дискретные состояния модели на уровне ее заданных частот дискретизации. Однако это не гарантирует, что решатель по умолчанию точно вычисляет непрерывные состояния модели. Поэтому вы, возможно, должны выбрать другой решатель, различный фиксированный размер шага, или и достигнуть приемлемой точности и приемлемого времени симуляции.
Фиксированный шаг Непрерывные Неявные Решатели. Неявный решатель вычисляет состояние на следующем временном шаге как неявная функция состояния на шаге текущего времени и производной состояния на следующем временном шаге. Другими словами:
Simulink предоставляет одному фиксированному шагу неявный решатель: ode14x. Этот решатель использует комбинацию метода Ньютона и экстраполяции от текущего значения, чтобы вычислить значение состояния на следующем временном шаге. Можно указать, что количество итераций метода Ньютона и экстраполяции приказывает, что использование решателя, чтобы вычислить следующее значение образцового состояния (см. размер Фиксированного шага (основной шаг расчета)). Чем больше итераций и выше порядок экстраполяции, который вы выбираете, тем больше точность вы получаете. Однако вы одновременно создаете большую вычислительную нагрузку на размер шага.
Любой фиксированный шаг непрерывные решатели в продукте Simulink может моделировать модель к любому желаемому уровню точности, учитывая достаточно небольшой размер шага. К сожалению, это не возможно или практично, чтобы решить без испытания, комбинации решателя и размера шага, который приведет к приемлемым результатам для непрерывных состояний в самое короткое время. Определение лучшего решателя для конкретной модели обычно требует экспериментирования.
Выбрать фиксированный шаг непрерывный решатель,
Выберите ошибочные допуски. Для получения дополнительной информации смотрите Ошибочные Допуски к Решателям Переменного Шага.
Используйте один из решателей переменного шага, чтобы моделировать вашу модель к уровню точности, которую вы хотите. Запустите с ode45. Если ваша модель медленно запускается, ваша проблема может быть жесткой и нуждаться в неявном решателе. Результаты этого шага дают хорошее приближение правильных результатов симуляции и соответствующего фиксированного размера шага.
Используйте ode1, чтобы моделировать вашу модель в размере шага по умолчанию для вашей модели. Сравните результаты симуляции для ode1 с симуляцией для решателя переменного шага. Если результатами является то же самое для заданного уровня точности, вы нашли лучший решатель фиксированного шага для своей модели, а именно, ode1. Вы приходите к этому выводу, потому что ode1 является самым простым из решателей фиксированного шага и следовательно приводит к самому короткому времени симуляции для текущего размера шага.
Если ode1 не дает удовлетворительные результаты, повторите предыдущие шаги с другими решателями фиксированного шага, пока вы не находите тот, который дает точные результаты с наименее вычислительным усилием. Самый эффективный способ выполнить эту задачу состоит в том, чтобы использовать метод двоичного поиска:
Попробуйте ode3.
Если ode3 дает точные результаты, попробуйте ode2. Если ode2 дает точные результаты, это - лучший решатель для вашей модели; в противном случае ode3 является лучшим.
Если ode3 не дает точные результаты, попробуйте ode5. Если ode5 дает точные результаты, попробуйте ode4. Если ode4 дает точные результаты, выберите его как решатель для вашей модели; в противном случае выберите ode5.
Если ode5 не дает точные результаты, уменьшает размер шага симуляции и повторяет предыдущий процесс. Продолжите таким образом, пока вы не находите решатель, который решает вашу модель точно с наименее вычислительным усилием.
Когда вы устанавливаете управление Типом панели настройки Решателя к Variable-step, управление Решателем позволяет вам выбирать один из решателей переменного шага. Как с решателями фиксированного шага, набор решателей переменного шага включает дискретный решатель и подмножество непрерывных решателей. Однако различающийся решатели фиксированного шага, размер шага отличается динамически на основе локальной ошибки.
Выбор между двумя типами решателей переменного шага зависит от того, ли блоки в ваших состояниях модели define и, если так, тип состояний, которые они задают. Если ваша модель не задает состояний или задает только дискретные состояния, выберите дискретный решатель. Если модель не имеет никаких состояний или только дискретных состояний, Simulink использует дискретный решатель, чтобы моделировать модель, даже если вы задаете непрерывный решатель. Если модель имеет непрерывные состояния, непрерывные решатели используют численное интегрирование, чтобы вычислить значения непрерывных состояний на следующем временном шаге.
Решатели переменного шага динамически отличаются размер шага во время симуляции. Каждый из этих решателей увеличивает или уменьшает размер шага с помощью своего локального контроля ошибок, чтобы достигнуть допусков, которые вы задаете. Вычисление размера шага на каждом временном шаге добавляет к вычислительным издержкам. Однако это может сократить общее количество шагов и время симуляции, требуемое поддержать заданный уровень точности.
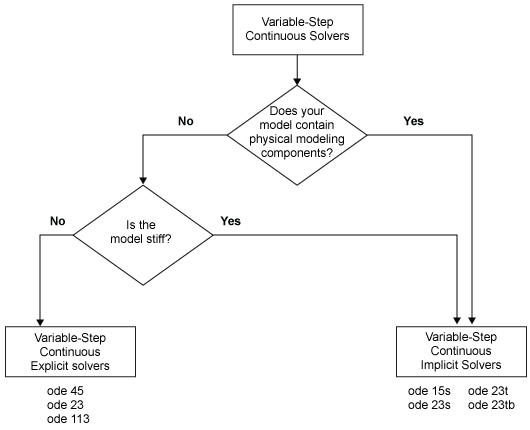
Можно далее категоризировать непрерывные решатели с переменным шагом как: один шаг или многоступенчатый, одноразрядный или переменный порядок, и явный или неявный. (См., Сравнивают Решатели для получения дополнительной информации.)
Переменный шаг явные решатели разработан для нежестких проблем. Simulink обеспечивает четыре таких решателя:
ode45
ode23
ode113
odeN
| Решатель ОДУ | Метод с одним шагом | Многоступенчатый метод | Порядок точности | Метод |
|---|---|---|---|---|
ode45 | X | Носитель | Рунге-Кутта, Dormand-принц (4,5) пара | |
ode23 | X | Низко | Рунге-Кутта (2,3) пара Bogacki & Shampine | |
ode113 | X | Переменная, низко к высоко | Реализация PECE Адамса-Бэшфорта-Маултона | |
odeN | X | Отошлите к порядку точности на Фиксированном Шаге непрерывные явные решатели | Отошлите к методу интегрирования на Фиксированном Шаге непрерывные явные решатели |
Хорошая эвристика для выбора решателя odeN, когда скорость симуляции важна:
Модель содержит много сброса решателя и/или нулевых пересечений
Solver Profiler не обнаруживает не пройдено шагов при профилировании модели
Если ваша проблема жестка, попытайтесь использовать один из переменного шага неявные решатели:
ode15s
ode23s
ode23t
ode23tb
| Решатель ОДУ | Метод с одним шагом | Многоступенчатый метод | Порядок точности | Метод сброса решателя | 'MaxOrder' | Метод |
|---|---|---|---|---|---|---|
ode15s | X | Переменная, от низкой к высокой | X | X | Числовые формулы дифференцирования (NDFs) | |
ode23s | X | Низко | Измененная формула Розенброка второго порядка | |||
ode23t | X | Низко | X | Метод трапеций с помощью “свободного” interpolant | ||
ode23tb | X | Низко | X | TR-BDF2 |
Метод Сброса решателя. Для трех из решателей для жестких проблем — ode15s, ode23t, и ode23tb — выпадающее меню для Solver reset method появляется на разделе Solver details панели Настройки. Этот параметр управляет, как решатель обрабатывает вызванный сброс, например, обнаружением пересечения нулем. Позволенными опциями является Fast и Robust. Fast указывает, что решатель не повторно вычисляет якобиан для сброса решателя, тогда как Robust указывает, что решатель делает. Следовательно, установка Fast в вычислительном отношении быстрее, но она может использовать размер небольшого шага в определенных случаях. Чтобы протестировать на такие случаи, запустите симуляцию с каждой установкой и сравните результаты. Если нет никакого различия в результатах, можно безопасно использовать установку Fast и сэкономить время. Если результаты значительно отличаются, попытайтесь уменьшать размер шага для быстрой симуляции.
Максимальный Порядок. Для решателя ode15s можно выбрать максимальный порядок числовых формул дифференцирования (NDFs), который применяет решатель. Поскольку ode15s использует сначала - через формулы пятого порядка, параметр Maximum order позволяет вам выбирать 1 through 5. Для жесткой проблемы можно хотеть запуститься с порядка 2.
Советы для Выбора Переменного Шага Неявный Решатель. Следующая таблица обеспечивает советы, относящиеся к приложению переменного шага неявные решатели. Для примера, сравнивающего поведение этих решателей, см. sldemo_solvers.
Для жесткой проблемы решения могут измениться на масштабе времени, который является очень небольшим по сравнению с интервалом интегрирования, в то время как решение интереса изменяется на намного более длительном масштабе времени. Методы, которые не разработаны для жестких проблем, неэффективны на интервалах, где решение медленно изменяется, потому что эти методы используют временные шаги, достаточно маленькие, чтобы разрешить самое быстрое изменение. Для получения дополнительной информации смотрите Шемпина, L. F. Числовое Решение Ordinary Differential Equations, Chapman & Hall, 1994.
Дискретные и непрерывные решатели переменного шага используют обнаружение пересечения нулем (см. Обнаружение Пересечения нулем) обрабатывать непрерывные сигналы.
Локальная Ошибка. Решатели переменного шага используют стандартные методы управления, чтобы контролировать локальную ошибку на каждом временном шаге. Во время каждого временного шага решатели вычисляют значения состояния в конце шага и определяют локальную ошибку — предполагаемая ошибка этих значений состояния. Они затем сравнивают локальную ошибку с приемлемой ошибкой, которая является функцией и относительного допуска (rtol) и абсолютного допуска (атолл). Если локальная ошибка больше, чем приемлемая ошибка для какого-либо состояния, решатель уменьшает размер шага и попробовал еще раз.
Относительный допуск измеряет ошибку относительно размера каждого состояния. Относительный допуск представляет процент значения состояния. Значение по умолчанию, 1e-3, означает, что вычисленное состояние точно в пределах 0,1%.
Абсолютный допуск является пороговым ошибочным значением. Этот допуск представляет приемлемую ошибку как значение измеренного нуля подходов состояния.
Решатели требуют, чтобы ошибка для i th состояние, ei, удовлетворила:
Следующие данные показывают график состояния и областей, в которых относительный допуск и абсолютный допуск определяют приемлемую ошибку.
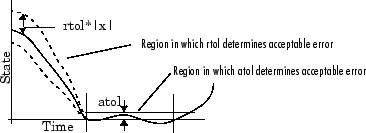
Абсолютные Допуски. Ваша модель имеет глобальный абсолютный допуск, который можно установить на панели Решателя диалогового окна Configuration Parameters. Этот допуск применяется ко всем состояниям в модели. Можно задать auto или действительный скаляр. Если вы задаете auto (значение по умолчанию), Simulink первоначально устанавливает абсолютный допуск к каждому состоянию на основе относительного допуска. Если относительный допуск является большим 1e-3, abstol инициализируется в 1e-6. Однако для reltol, меньшего, чем 1e-3, abstol для состояния инициализируется в reltol * 1e-3. В то время как симуляция прогрессирует, абсолютный допуск к каждому состоянию сброс к максимальному значению, которое состояние приняло до сих пор, времена относительный допуск к тому состоянию. Таким образом, если изменения состояния от 0 до 1 и reltol являются 1e-3, abstol инициализирует в 1e-6, и к концу симуляции достигает 1e-3 также. Если состояние идет от 0 до 1 000, то изменения abstol в 1.
Теперь, если изменения состояния от 0 до 1 и reltol установлены в 1e-4, то abstol инициализирует в 1e-7, и к концу симуляции достигает значения 1e-4.
Если вычисленное начальное значение для абсолютного допуска не подходит, можно определить соответствующее значение сами. Вам придется запустить симуляцию несколько раз, чтобы определить соответствующее значение для абсолютного допуска. Можно также задать, должен ли абсолютный допуск адаптироваться подобный его установке auto путем включения или отключения параметра AutoScaleAbsTol. Для получения дополнительной информации смотрите Автоматическую шкалу абсолютный допуск.
Несколько блоков позволяют вам указывать, что абсолютные значения допуска для решения модели утверждают, что они вычисляют или которые определяют их вывод:
Абсолютные значения допуска, которые вы задаете для этих блоков, заменяют глобальные настройки в диалоговом окне Configuration Parameters. Вы можете хотеть заменить глобальную установку, если, например, глобальная установка не обеспечивает достаточный контроль ошибок для всех ваших образцовых состояний, потому что они значительно различаются в значении. Можно установить блок абсолютный допуск на:
auto
– 1 (тот же as auto)
positive scalar
real vector (имеющий размерность равняются количеству соответствующих непрерывных состояний в блоке),
Советы. Если вы действительно принимаете решение установить абсолютный допуск, иметь в виду, что слишком низко значения заставляет решатель делать слишком много шагов около значений почти нулевого состояния. В результате симуляция медленнее.
С другой стороны, если вы устанавливаете абсолютный допуск слишком высоко, ваши результаты могут быть неточными как одно или несколько непрерывных состояний в вашем образцовом нуле подхода.
Если симуляция завершена, можно проверить точность результатов путем сокращения абсолютного допуска и выполнения симуляции снова. Если результаты этих двух симуляций удовлетворительно близки, то можно чувствовать себя уверенно в их точности.
Для неявных решателей Simulink должен вычислить якобиан решателя, который является субматрицей якобиевской матрицы, сопоставленной с непрерывным представлением модели Simulink. В целом это непрерывное представление имеет форму:
Якобиан, J, сформированный из этой системы уравнений:
В свою очередь якобиан решателя является субматрицей, .
Разреженность якобиана. Для многих физических систем якобиан решателя Jx разрежен, означая, что многие элементы Jx являются нулем.
Рассмотрите следующую систему уравнений:
От этой системы можно вывести шаблон разреженности, который отражает структуру уравнений. Шаблон, Булева матрица, имеет 1 для каждого это появляется явным образом на правой стороне уравнения. Поэтому вы достигаете:
Как обсуждено в полных и Разреженных Методах Возмущения и Полных и Разреженных Аналитических Методах соответственно, Разреженный Метод Возмущения и Разреженный Аналитический Метод могут смочь использовать в своих интересах этот шаблон разреженности, чтобы сократить количество необходимых вычислений и улучшать производительность.
Когда вы выбираете неявный решатель из панели Solver диалогового окна параметров конфигурации, параметр под названием Solver Jacobian method и выпадающее меню появляется. Это меню имеет пять опций для вычисления якобиана решателя:
auto
Sparse perturbation
Full perturbation
Sparse analytical
Full analytical
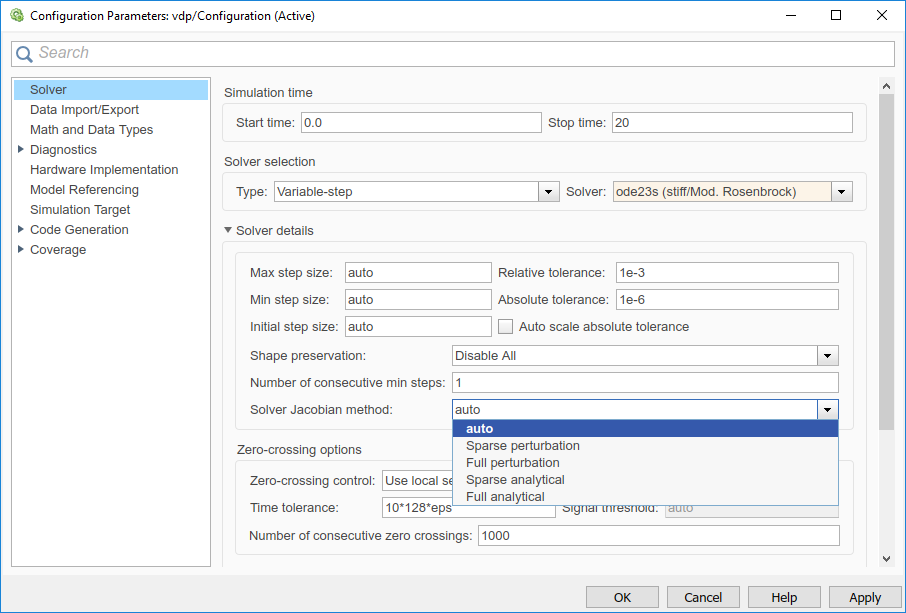
Если вы устанавливаете Automatic solver parameter selection на error в панели Диагностики Решателя, и вы выбираете метод другого решателя, чем Simulink, можно получить ошибку.
Ограничения. Методам якобиана решателя сопоставили следующие ограничения с ними.
Если вы выбираете аналитический якобиевский метод, но один или несколько блоков в модели не имеют аналитического якобиана, то Simulink применяет метод возмущения.
Если вы выбираете разреженное возмущение, и ваша модель содержит блоки хранилища данных, Simulink применяет полный метод возмущения.
Настройкой по умолчанию для Solver Jacobian method является auto. Выбор этого выбора заставляет Simulink выполнять эвристику, чтобы определить, какой из остающихся четырех методов лучше всего удовлетворяет вашей модели. Этот алгоритм изображен в следующей блок-схеме.
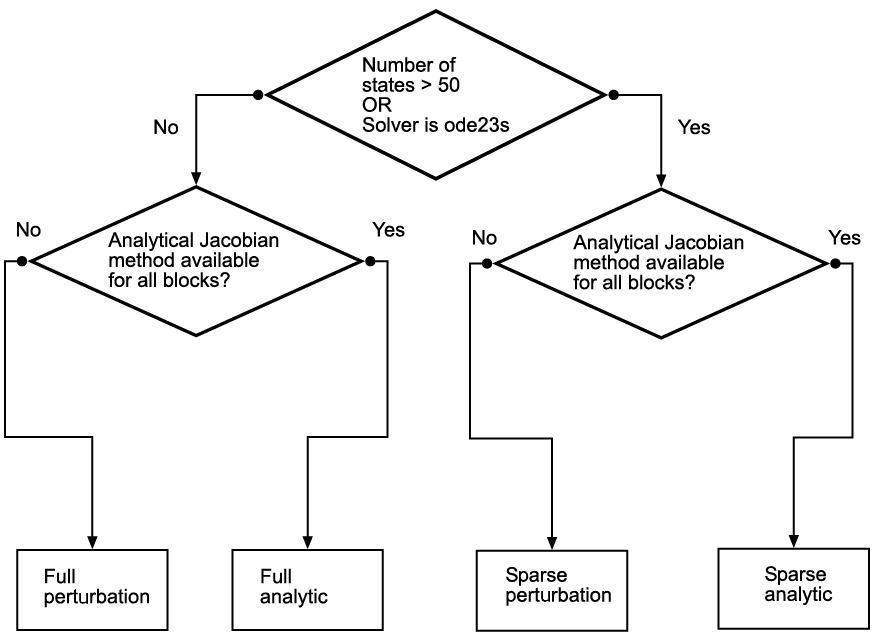
Поскольку разреженные методы выгодны для моделей, имеющих большое количество состояний, если 50 или больше состояний существуют в вашей модели, эвристика выбирает разреженный метод. Логика также приводит к разреженному методу, если вы задаете ode23s, потому что, в отличие от других неявных решателей, ode23s генерирует новый якобиан на каждом временном шаге. Разреженное аналитическое или разреженный метод возмущения, поэтому, очень выгодны. Эвристика также гарантирует, что аналитические методы используются, только если каждый блок в вашей модели может сгенерировать аналитический якобиан.
Полный метод возмущения был стандартным численным методом, что Simulink раньше решал систему. Для этого метода Simulink решает полный набор уравнений возмущения и использует LAPACK для линейных алгебраических операций. Этот метод является дорогостоящим с вычислительной точки зрения, но это остается рекомендуемый метод для установления базовых результатов.
Разреженный метод возмущения пытается улучшать производительность во время выполнения путем пользования преимуществами математическим премуществом разреженного якобиевского шаблона. Возврат демонстрационной системе трех уравнений и трех состояний,
Якобиан решателя:
|
|
Поэтому, необходимо встревожить каждое из трех состояний три раза и выполнить производную функцию три раза. Для системы с состояниями n этот метод тревожит состояния времена n.
Путем применения шаблона разреженности и беспокойства состояний x 1 и x 2 вместе, эта матрица уменьшает до:
|
|
Решатель может теперь решить столбцы 1 и 2 в одной развертке. В то время как разреженный метод возмущения сохраняет значительное вычисление, он также добавляет наверху к компиляции. Это может даже замедлить симуляцию, если система не имеет большого количества непрерывных состояний. Переломный момент существует, для которого вы получаете увеличенную производительность путем применения этого метода. В целом системы, имеющие большое количество непрерывных состояний, обычно разреженны и преимущество из разреженного метода.
Разреженный метод возмущения, как разреженный аналитический метод, использует UMFPACK, чтобы выполнить линейные алгебраические операции. Кроме того, разреженный метод возмущения поддерживает и RSim и Быстрый Режим Accelerator.
Полные и разреженные аналитические методы пытаются улучшать производительность путем вычисления якобиевских использующих аналитических уравнений, а не уравнений возмущения. Разреженный аналитический метод, также использует информацию о разреженности, чтобы ускорить линейные алгебраические операции, требуемые решить обыкновенные дифференциальные уравнения.
Для получения дополнительной информации о том, как получить доступ и интерпретировать шаблон разреженности в MATLAB®, см. sldemo_metro.
В то время как разреженный метод возмущения поддерживает RSim, разреженный аналитический метод не делает. Следовательно, независимо от которого разреженного метода вы выбираете, любой сгенерированный код использует разреженный метод возмущения. Это ограничение применяется к Быстрому Режиму Accelerator также.