Документация

Загрузка демонстрационных данных.

Загрузите демонстрационные данные о панели.

load panelData

Массив набора данных, panelData, содержит ежегодные наблюдения относительно восьми городов в течение 6 лет. Это - моделируемые данные.

Задайте переменные.

Первая переменная, Growth, измеряет экономический рост (переменная отклика). Вторые и третьи переменные являются городом и индикаторами года, соответственно. Последняя переменная, Employ, измеряет занятость (переменная прогноза).

y = panelData.Growth;
city = panelData.City;
year = panelData.Year;
x = panelData.Employ;

Отобразите на графике данные, сгруппированные по категориям.

Чтобы искать потенциальные специфичные для города фиксированные эффекты, создайте диаграмму ответа, сгруппированного городом.

figure()
boxplot(y,city)
xlabel('City')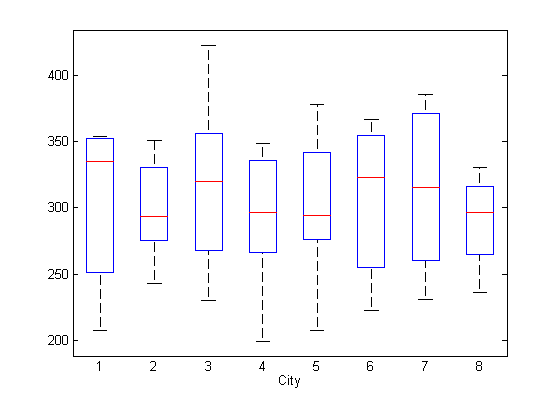

Кажется, нет никаких систематических различий в среднем ответе среди городов.

Отобразите на графике данные, сгруппированные различной категорией.

Чтобы искать потенциальные специфичные для года фиксированные эффекты, создайте диаграмму ответа, сгруппированного годом.

figure()
boxplot(y,year)
xlabel('Year')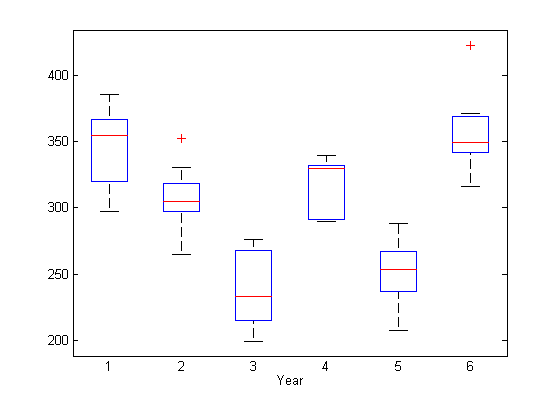

Некоторое доказательство систематических различий в среднем ответе между годами, кажется, существует.

Данные об ответе формата.

Позвольте _yij обозначить ответ для города j = 1..., d, в году i = 1..., n. Точно так же _xij является соответствующим значением переменной прогноза. В этом примере, n = 6 и d = 8.

Рассмотрите подбор кривой специфичной для года фиксированной модели эффектов с постоянным склоном и параллельной корреляцией среди городов в том же году,

где $${\epsilon }_i=({\epsilon }_{i1},\dots ,{\epsilon }_{id}{)}^{\prime }\sim MVN(0,\Sigma )$$. Параллельная корреляция учитывает любые неизмеренные, статические временем факторы, которые могут повлиять на рост так же для некоторых городов. Например, города с близкой пространственной близостью могут быть более вероятны иметь подобный экономический рост.

Чтобы соответствовать этой модели с помощью mvregress, измените данные об ответе в n-by-d матрица.

n = 6; d = 8;
Y = reshape(y,n,d);

Матрицы проекта формата.

Создайте массив ячеек длины-n d-by-K матрицы проекта. Для этой модели существует K = 7 параметров (d = 6 условий прерывания и наклон).

Предположим, что вектор параметров располагается как

В этом случае первая матрица проекта в течение года 1 похожа

и вторая матрица проекта в течение года 2 похожа

Матрицы проекта в течение остающихся 4 лет подобны.

K = 7; N = n*d;
X = cell(n,1);
for i = 1:n
    x0 = zeros(d,K-1);
    x0(:,i) = 1;
    X{i} = [x0,x(i:n:N)];
end

Соответствуйте модели.

Соответствуйте модели с помощью обычных наименьших квадратов (OLS).

[b,sig,E,V] = mvregress(X,Y,'algorithm','cwls');
b

b =

   41.6878
   26.1864
  -64.5107
   11.0924
  -59.1872
   71.3313
    4.9525

Постройте подобранную модель.

xx = linspace(min(x),max(x));
axx = repmat(b(1:K-1),1,length(xx));
bxx = repmat(b(K)*xx,n,1);
yhat =  axx + bxx;

figure()
hPoints = gscatter(x,y,year);
hold on
hLines = plot(xx,yhat);
for i=1:n  
   set(hLines(i),'color',get(hPoints(i),'color'));
end
hold off

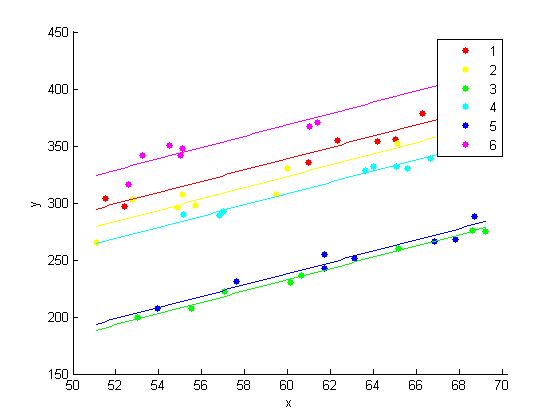
Модель со специфичными для года прерываниями и общим наклоном, кажется, соответствует данным вполне хорошо.

Остаточная корреляция.

Постройте невязки, сгруппированные годом.

figure()
gscatter(year,E(:),city)
ylabel('Residuals')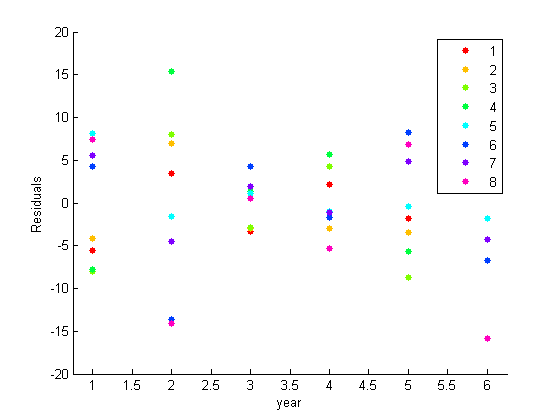

Остаточный график предполагает, что параллельная корреляция присутствует. Для примеров города 1, 2, 3, и 4 последовательно выше или ниже среднего значения как группа в любом данном году. То же самое верно для набора городов 5, 6, 7, и 8. Как замечено в исследовательских графиках, нет никаких систематических специфичных для города эффектов.

Панель исправила стандартные погрешности.

Используйте предполагаемую ошибочную ковариационную матрицу отклонения, чтобы вычислить исправленные стандартные погрешности панели для коэффициентов регрессии.

XX = cell2mat(X);
S = kron(eye(n),sig);
Vpcse = inv(XX'*XX)*XX'*S*XX*inv(XX'*XX);
se = sqrt(diag(Vpcse))

se =

    9.3750
    8.6698
    9.3406
    9.4286
    9.5729
    8.8207
    0.1527