Настройте многомерные проблемы регрессии

Матрица ответа

Чтобы соответствовать многомерной модели линейной регрессии использование mvregress, необходимо настроить матрицу ответа и матрицы проекта конкретным способом. Учитывая правильно отформатированные входные параметры, mvregress может решить множество многомерных проблем регрессии.

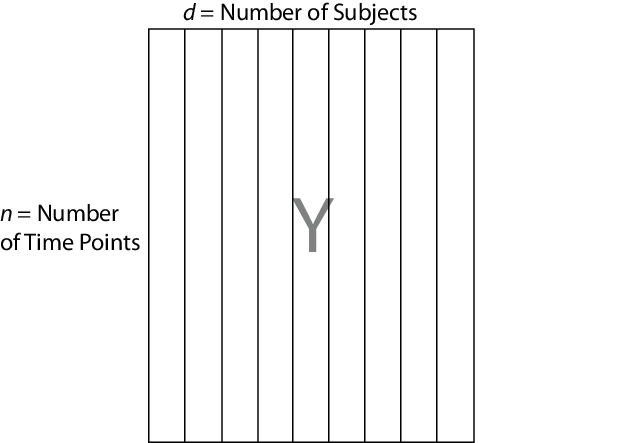
mvregress ожидает, что наблюдения n за потенциально коррелированым d - размерные ответы будут в n-by-d матрица, названная Y, например. Таким образом, настройте свои ответы так, чтобы структура зависимости была между наблюдениями в той же строке. Если вы задаете Y как вектор длины n (или строка или вектор-столбец), то mvregress принимает, что d = 1, и обрабатывает элементы как n независимые наблюдения. Это не моделирует вектор как одну реализацию коррелированого ряда (такого как временные ряды).

Чтобы проиллюстрировать, как настроить матрицу ответа, предположите, что ваши многомерные ответы являются повторенными измерениями, сделанными на предметах в нескольких моментах времени, как в следующей фигуре.

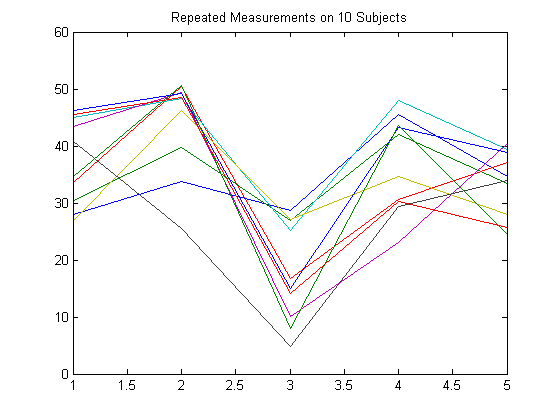
Предположим, что наблюдения в предмете коррелируются.

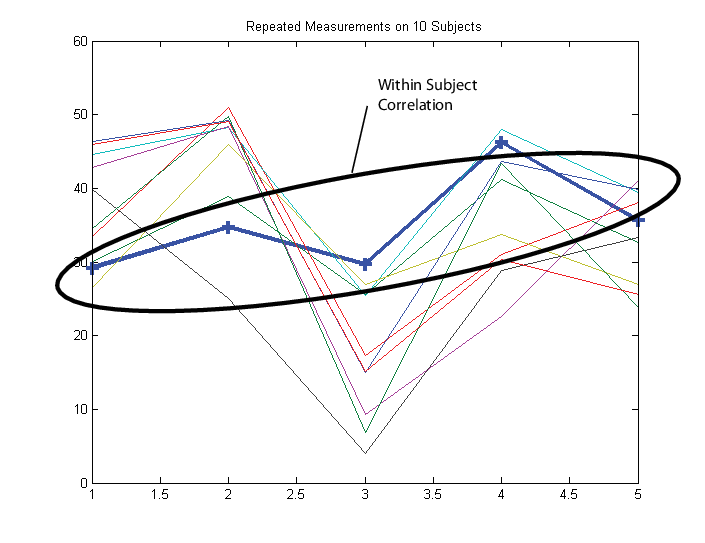
В этом случае настройте матрицу ответа Y, таким образом, что каждая строка соответствует предмету, и каждый столбец соответствует моменту времени.

С другой стороны предположите, что наблюдения, сделанные на предметах одновременно, коррелируются (параллельная корреляция).

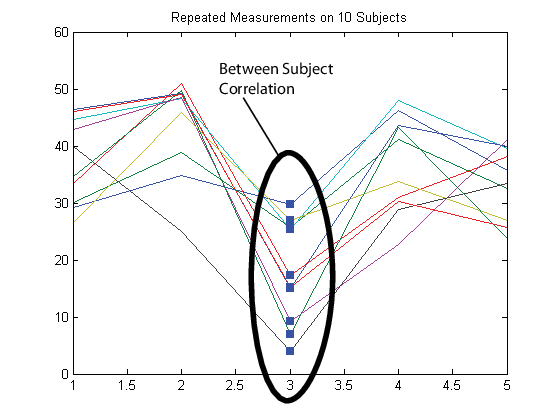
В этом случае настройте матрицу ответа Y, таким образом, что каждая строка соответствует моменту времени, и каждый столбец соответствует предмету.

Разработайте матрицы

В многомерной модели линейной регрессии каждом d - размерный ответ имеет соответствующую матрицу проекта. В зависимости от модели проекта матричная сила состоять из внешних переменных прогноза, фиктивных переменных, изолировала ответы или комбинацию этих и других ковариационных условий.

Если d> 1 и все размерности d имеет ту же матрицу проекта, то задает один n-by-p матрица проекта, где p является количеством переменных прогноза. Чтобы определить прерывание для каждой размерности, добавьте столбец из единиц к матрице проекта. В этом случае mvregress применяет матрицу проекта ко всем размерностям d.
Если d> 1 и все размерности d не имеет той же матрицы проекта, то задайте матрицы проекта с помощью массива ячеек длины-n d-by-K массивы, названные X, например. K является общим количеством коэффициентов регрессии в модели. Обратите внимание на то, что строки массивов в X соответствуют столбцам матрицы ответа, Y.

Если все наблюдения n имеют ту же матрицу проекта, можно задать массив ячеек, содержащий один d-by-K матрица проекта. В этом случае mvregress применяет матрицу проекта ко всем наблюдениям n. Например, эта ситуация может возникнуть, если предикторы являются функциями времени, и все наблюдения были измерены одновременно точки.
В особом случае, что d = 1, можно задать один n-by-K матрица проекта (не в массиве ячеек). Однако необходимо рассмотреть использование fitlm, чтобы соответствовать моделям регрессии к одномерным, непрерывным ответам.

Следующие разделы иллюстрируют, как настроить некоторые общие многомерные проблемы регрессии для оценки с помощью mvregress.

Многомерная общая линейная модель

Многомерная общая линейная модель имеет форму

$Y_{n \times d} = X_{n \times (p + 1)} B_{(p + 1) \times d} + E_{n \times d} .$

В расширенной форме,

$[\begin{array}{l} y_{11} y_{12} \dots y_{1 d} \\ y_{21} y_{22} \dots y_{2 d} \\ ⋮ ⋮ ⋱ ⋮ \\ y_{n 1} y_{n 2} \dots y_{n d} \end{array}] = [\begin{array}{l} 1 x_{11} x_{12} \dots x_{1 p} \\ 1 x_{21} x_{22} \dots x_{2 p} \\ ⋮ ⋮ ⋮ ⋱ ⋮ \\ 1 x_{n 1} x_{n 2} \dots x_{n p} \end{array}] [\begin{array}{l} β_{01} β_{02} \dots β_{0 d} \\ β_{11} β_{12} \dots β_{1 d} \\ ⋮ ⋮ ⋱ ⋮ \\ β_{p 1} β_{p 2} \dots β_{p d} \end{array}] + [\begin{array}{l} ε_{11} ε_{12} \dots ε_{1 d} \\ ε_{21} ε_{22} \dots ε_{2 d} \\ ⋮ ⋮ ⋱ ⋮ \\ ε_{n 1} ε_{n 2} \dots ε_{n d} \end{array}] .$

Таким образом, каждый d - размерный ответ имеет прерывание и переменные прогноза p, и каждая размерность имеет свой собственный набор коэффициентов регрессии. В этой форме решением методом наименьших квадратов является B = X\Y. Чтобы оценить эту модель с помощью mvregress, используйте n-by-d матрица ответов, как выше.

Если все размерности d имеют ту же матрицу проекта, используйте n (p +1) матрица проекта, как выше. Добавление столбца из единиц к переменным прогноза p вычисляет прерывание для каждой размерности.

Если все размерности d не имеют той же матрицы проекта, переформатируйте n (p + 1) матрица проекта в массив ячеек длины-n d-by-K матрицы. Здесь, K = (p + 1) d для прерывания и наклоны для каждой размерности.

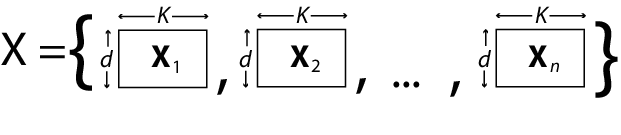
Например, предположите n = 4, d = 3, и p = 2 (два условия предиктора в дополнение к прерыванию). Эти данные показывают, как отформатировать i th элемент в массиве ячеек.

Если вы предпочитаете, можно изменить K-by-1 вектор коэффициентов назад в (p + 1)-by-d матрица после оценки.

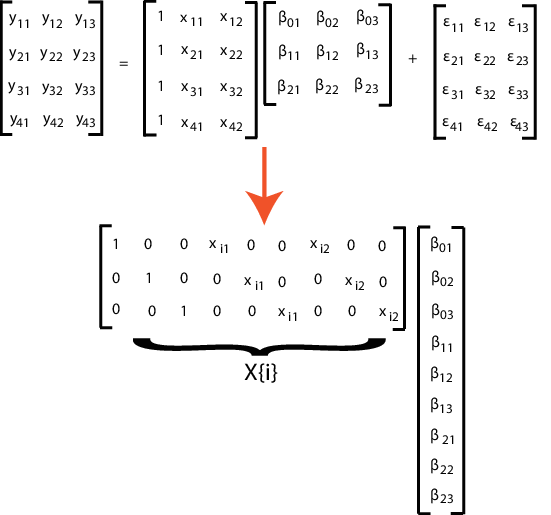
Чтобы поместить ограничения на параметры модели, настройте матрицу проекта соответственно. Например, предположите, что три измерения в предыдущем примере имеют общий наклон. Таким образом, $β_{11} = β_{12} = β_{13} = β_{1}$ и $β_{21} = β_{22} = β_{23} = β_{2} .$ В этом случае каждая матрица проекта 3 на 5, как показано в следующей фигуре.

Продольный анализ

В продольном анализе вы можете измерить ответы на предметах n в моментах времени d с корреляцией между наблюдениями, сделанными на том же предмете. Например, предположите, что вы измеряете ответы _yij во времена _tij, i = 1..., n и j = 1..., d. Кроме того, предположите, что каждый предмет находится в одной из двух групп (таких как штекер или розетка), задан переменной _Gi индикатора. Вы могли смоделировать _yij как функцию _Gi и _tij, со специфичными для группы прерываниями и наклонами, можно следующим образом:

$y_{i j} = β_{0} + β_{1} G_{i} + β_{2} t_{i j} + β_{3} G_{i} \times t_{i j} + ε_{i j}, i = 1, \dots, n; j = 1, \dots, d,$

где

$ε_{i} = (ε_{i 1}, \dots, ε_{i d})^{'} \sim M V N (0, Σ) .$

Большинство продольных моделей включает время как явный предиктор.

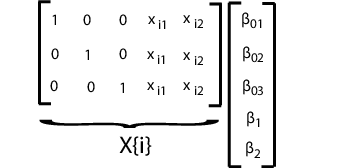
Чтобы соответствовать этой модели с помощью mvregress, расположите ответы в n-by-d матрица, где n является количеством предметов, и d является количеством моментов времени. Задайте матрицы проекта в n - массив ячеек длины d-by-K матрицы, где здесь K = 4 для этих четырех коэффициентов регрессии.

Например, предположите d = 5 (пять наблюдений на предмет). i th проект матричный и соответствующий вектор параметра для заданной модели показывают в следующей фигуре.

Анализ панели

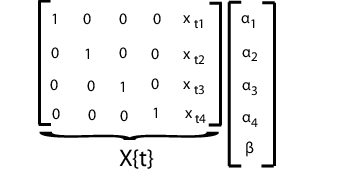
В анализе панели вы можете измерить ответы и коварианты на предметах d (таких как люди или страны) в моментах времени n. Например, предположите, что вы измеряете ответы _ytj и коварианты _xtj на предметах j = 1..., d во времена t = 1..., n. Фиксированная модель панели эффектов, с подчинено-специфичными фиксированными эффектами и параллельной корреляцией может быть похожей:

$y_{t j} = α_{j} + β x_{t j} + ε_{t j},$

где

$ε_{t} = (ε_{t 1}, ..., ε_{t d})^{'} \sim M V N (0, Σ) .$

В отличие от продольных моделей, аналитическая модель панели обычно включает коварианты, измеренные в каждый момент времени, вместо того, чтобы использовать время в качестве явного предиктора.

Чтобы соответствовать этой модели с помощью mvregress, расположите ответы в n-by-d матрица, такая, что каждый столбец соответствует предмету. Задайте матрицы проекта в n - массив ячеек длины d-by-K матрицы, где здесь K = d + 1 для прерываний d и наклонного термина.

Например, предположите d = 4 (четыре предмета). t th проект матричный и соответствующий вектор параметра показывают в следующей фигуре.

На вид Несвязанная регрессия

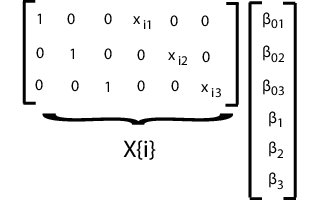
В на вид несвязанной регрессии (SUR), вы модель d разделяют регрессии, каждого с ее собственным прерыванием и наклоном, но ковариационной матрицей отклонения распространенной ошибки. Например, предположите, что вы измеряете ответы _yij и коварианты _xij для моделей j регрессии = 1..., d, с i = 1..., наблюдения n, чтобы соответствовать каждой регрессии. Модель SUR может быть похожей:

$y_{i j} = β_{0 j} + β_{j} x_{i j} + ε_{i j},$

где

$ε_{i} = (ε_{i 1}, \dots, ε_{i d})^{'} \sim M V N (0, Σ) .$

Эта модель очень похожа на многомерную общую линейную модель, за исключением того, что это имеет различные коварианты для каждой размерности.

Чтобы соответствовать этой модели с помощью mvregress, расположите ответы в n-by-d матрица, такая, что каждый столбец имеет данные для j th модель регрессии. Задайте матрицы проекта в n - массив ячеек длины d-by-K матрицы, где здесь K = 2d для прерываний d и d клонится.

Например, предположите d = 3 (три регрессии). i th проект матричный и соответствующий вектор параметра показывают в следующей фигуре.

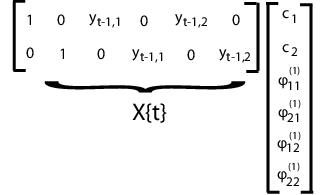
Векторная авторегрессивная модель

VAR (p), векторная авторегрессивная модель выражает d - размерные ответы временных рядов как линейная функция p, изолировал d - размерные ответы с предыдущих раз. Например, предположите, что вы измеряете ответы _ytj для временных рядов j = 1..., d во времена t = 1..., n. Модель VAR (p) может быть похожей:

$[\begin{array}{l} y_{t 1} \\ y_{t 2} \\ ⋮ \\ y_{t d} \end{array}] = [\begin{array}{l} c_{1} \\ c_{} \\ 2 ⋮ \\ c_{d} \end{array}] + [\begin{array}{l} φ_{11}^{(1)} φ_{12}^{(1)} \dots φ_{1 d}^{(1)} \\ ⋮ ⋮ ⋱ ⋮ \\ φ_{d 1}^{(1)} φ_{d 2}^{(1)} \dots φ_{d d}^{(1)} \end{array}] [\begin{array}{l} y_{t - 1, 1} \\ y_{t - 1, 2} \\ ⋮ \\ y_{t - 1, d} \end{array}] + \dots + [\begin{array}{l} φ_{11}^{(p)} φ_{12}^{(p)} \dots φ_{1 d}^{(p)} \\ ⋮ ⋮ ⋱ ⋮ \\ φ_{d 1}^{(p)} φ_{d 2}^{(p)} \dots φ_{d d}^{(p)} \end{array}] [\begin{array}{l} y_{t - p, 1} \\ y_{t - p, 2} \\ ⋮ \\ y_{t - p, d} \end{array}] + [\begin{array}{l} ε_{t 1} \\ ε_{t 2} \\ ⋮ \\ ε_{t d} \end{array}],$

где

$ε_{t} = (ε_{t 1}, ..., ε_{t d})^{'} \sim M V N (0, Σ) .$

При оценке векторных авторегрессивных моделей обычно необходимо использовать первые наблюдения p, чтобы инициировать модель или обеспечить некоторые другие преддемонстрационные значения ответа.

Чтобы соответствовать этой модели с помощью mvregress, расположите ответы в n-by-d матрица, такая, что каждый столбец соответствует временным рядам. Задайте матрицы проекта в n - массив ячеек длины d-by-K матрицы, где здесь K = d + ^pd2.

Например, предположите d = 2 (два временных рядов) и p = 1 (одна задержка). t th проект матричный и соответствующий вектор параметра показывают в следующей фигуре.

Также Econometrics Toolbox™ имеет функции для подбора кривой и прогнозирования моделей VAR (p), включая опцию, чтобы задать внешние переменные прогноза.

Смотрите также

mvregress | mvregresslike

Документация