Документация

Загрузка демонстрационных данных.

Загрузите выборочные данные. Данные включают оценки для 9 различных индикаторов качества жизни в 329 американских городах. Это климат, корпус, здоровье, преступление, транспортировка, образование, искусства, воссоздание и экономика. Для каждой категории более высокая оценка лучше. Например, более высокая оценка для преступления означает более низкий уровень преступности.

Отобразите переменную categories.

load cities
categories

categories =
   climate       
   housing       
   health        
   crime         
   transportation
   education     
   arts          
   recreation    
   economics   

Всего, набор данных cities содержит три переменные:

Отображение данных на графике.

Сделайте коробчатую диаграмму, чтобы посмотреть на распределение данных ratings.

figure()
boxplot(ratings,'Orientation','horizontal','Labels',categories)

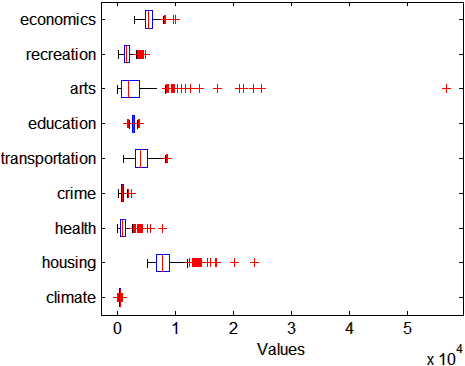
Существует больше изменчивости в оценках искусств и корпуса, чем в оценках преступления и климата.

Проверяйте попарную корреляцию.

Проверяйте попарную корреляцию между переменными.

C = corr(ratings,ratings);

Корреляция среди некоторых переменных является целых 0.85. Анализ основных компонентов создает независимые новые переменные, которые являются линейными комбинациями исходных переменных.

Вычислите основные компоненты.

Когда все переменные находятся в том же модуле, уместно вычислить основные компоненты для необработанных данных. Когда переменные находятся в различных модулях, или различие в отклонении различных столбцов является существенным (как в этом случае), масштабирование данных или использование весов часто предпочтительны.

Выполните анализ главных компонентов при помощи обратных отклонений оценок как веса.

w = 1./var(ratings);
[wcoeff,score,latent,tsquared,explained] = pca(ratings,...
'VariableWeights',w);

Или эквивалентно:

[wcoeff,score,latent,tsquared,explained] = pca(ratings,...
'VariableWeights','variance');

Следующие разделы объясняют пять выходных параметров pca.

Коэффициенты компонента.

Первый вывод, wcoeff, содержит коэффициенты основных компонентов.

Первые три вектора коэффициентов основного компонента:

c3 = wcoeff(:,1:3)

c3 = wcoeff(:,1:3)
c3 =

   1.0e+03 *

    0.0249   -0.0263   -0.0834
    0.8504   -0.5978   -0.4965
    0.4616    0.3004   -0.0073
    0.1005   -0.1269    0.0661
    0.5096    0.2606    0.2124
    0.0883    0.1551    0.0737
    2.1496    0.9043   -0.1229
    0.2649   -0.3106   -0.0411
    0.1469   -0.5111    0.6586

Эти коэффициенты взвешиваются, следовательно матрица коэффициентов не ортонормирована.

Преобразуйте коэффициенты.

Преобразуйте коэффициенты так, чтобы они были ортонормированы.

 coefforth = inv(diag(std(ratings)))*wcoeff;

Обратите внимание на то, что, если вы используете вектор весов, w, при проведении pca, затем

 coefforth = diag(sqrt(w))*wcoeff;

Проверяйте, что коэффициенты ортонормированы.

Преобразованные коэффициенты теперь ортонормированы.

I = coefforth'*coefforth;
I(1:3,1:3)

ans =
    1.0000   -0.0000   -0.0000
   -0.0000    1.0000   -0.0000
   -0.0000   -0.0000    1.0000

Очки компонента.

Второй вывод, score, содержит координаты исходных данных в новой системе координат, заданной основными компонентами. Матрица score одного размера как матрица входных данных. Можно также получить очки компонента с помощью ортонормированных коэффициентов и стандартизированных оценок можно следующим образом.

cscores = zscore(ratings)*coefforth;

cscores и score являются идентичными матрицами.

Постройте очки компонента.

Создайте график первых двух столбцов score.

figure()
plot(score(:,1),score(:,2),'+')
xlabel('1st Principal Component')
ylabel('2nd Principal Component')

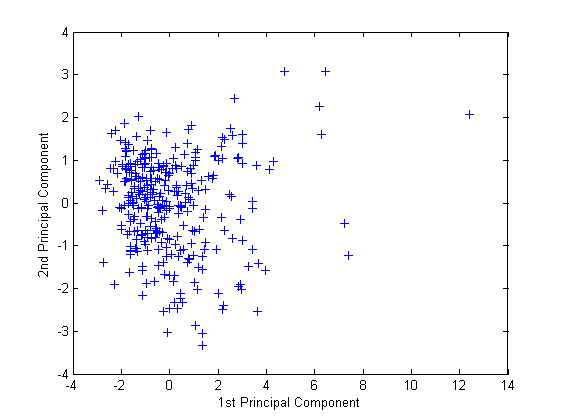
Этот график показывает и масштабированные данные об оценках в центре, спроектированные на первые два основных компонента. pca вычисляет очки, чтобы иметь средний нуль.

Исследуйте график в интерактивном режиме.

Отметьте отдаленные точки в правильной половине графика. Можно графически идентифицировать эти точки можно следующим образом.

gname

Переместите свой курсор через график и нажатие кнопки однажды около самых правых семи точек. Это маркирует точки их номерами строк как в следующей фигуре.

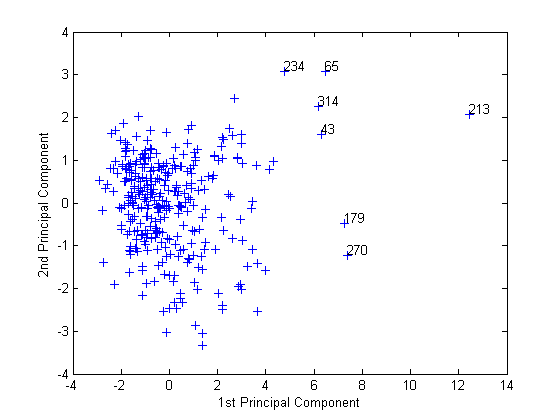
После маркировки точек нажмите Return.

Извлеките имена наблюдения.

Создайте индексную переменную, содержащую номера строк всех городов, которые вы выбрали, и получите имена городов.

metro = [43 65 179 213 234 270 314];
names(metro,:)

ans =
   Boston, MA                  
   Chicago, IL                 
   Los Angeles, Long Beach, CA 
   New York, NY                
   Philadelphia, PA-NJ         
   San Francisco, CA           
   Washington, DC-MD-VA

Эти маркированные города являются некоторыми самыми большими центрами сосредоточения населения в Соединенных Штатах, и они кажутся более экстремальными, чем остаток от данных.

Отклонения компонента.

Третий вывод, latent, является вектором, содержащим отклонение, объясненное соответствующим основным компонентом. Каждый столбец score имеет демонстрационное отклонение, равное соответствующей строке latent.

latent

latent =

    3.4083
    1.2140
    1.1415
    0.9209
    0.7533
    0.6306
    0.4930
    0.3180
    0.1204

Отклонение процента объяснено.

Пятый вывод, explained, является вектором, содержащим отклонение процента, объясненное соответствующим основным компонентом.

explained

explained =

   37.8699
   13.4886
   12.6831
   10.2324
    8.3698
    7.0062
    5.4783
    3.5338
    1.3378

Создайте график каменистой осыпи.

Сделайте график каменистой осыпи изменчивости процента объясненным каждым основным компонентом.

figure()
pareto(explained)
xlabel('Principal Component')
ylabel('Variance Explained (%)')

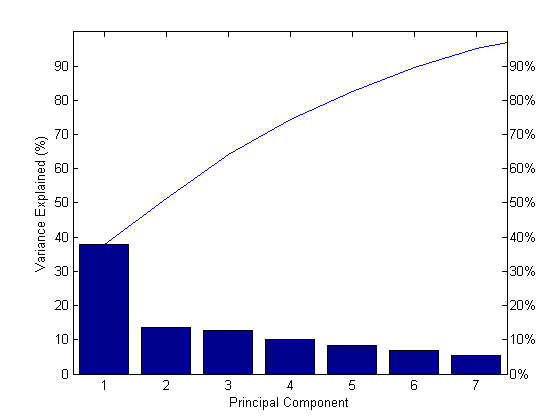
Этот график каменистой осыпи только показывает первые семь (вместо общих девяти) компоненты, которые объясняют 95% общего отклонения. Единственный ясный перерыв в количестве отклонения, составляемого каждым компонентом, между первыми и вторыми компонентами. Однако первый компонент отдельно объясняет меньше чем 40% отклонения, таким образом, больше компонентов может быть необходимо. Вы видите, что первые три основных компонента объясняют примерно две трети общей изменчивости в стандартизированных оценках, так, чтобы мог быть разумный способ уменьшать размерности.

Статистическая величина Хотеллинга T-squared.

Последним выводом от pca является tsquared, который является ^T2 Хотеллинга, статистической мерой многомерного расстояния каждого наблюдения от центра набора данных. Это - аналитический способ найти наиболее экстремальные точки в данных.

[st2,index] = sort(tsquared,'descend'); % sort in descending order
extreme = index(1);
names(extreme,:)

ans =

New York, NY

Оценки для Нью-Йорка являются самыми далекими из среднего американского города.

Визуализируйте результаты.

Визуализируйте и ортонормированные коэффициенты основного компонента для каждой переменной и музыку основного компонента к каждому наблюдению в одном графике.

biplot(coefforth(:,1:2),'Scores',score(:,1:2),'Varlabels',categories);
axis([-.26 0.6 -.51 .51]);

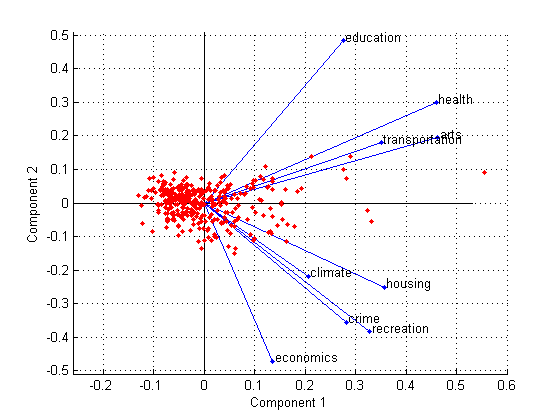
Все девять переменных представлены в этом bi-графике вектора, и направление и длина вектора указывают, как каждая переменная способствует этим двум основным компонентам в графике. Например, первый основной компонент, на горизонтальной оси, имеет положительные коэффициенты для всех девяти переменных. Именно поэтому эти девять векторов направлены в правильную половину графика. Самые большие коэффициенты в первом основном компоненте являются третьими и седьмыми элементами, соответствуя переменным health и arts.

Второй основной компонент, на вертикальной оси, имеет положительные коэффициенты для переменных education, health, arts, и transportation и отрицательных коэффициентов для остающихся пяти переменных. Это указывает, что второй компонент различает города, которые имеют высокие значения для первого набора переменных и низко для второго, и города, которые имеют противоположное.

Переменные метки в этой фигуре несколько переполнены. Можно или исключить аргумент пары "имя-значение" VarLabels при создании графика, или выбрать и перетащить некоторые метки к лучшим позициям с помощью Графического инструмента Редактирования от панели инструментов окна рисунка.

Этот 2D bi-график также включает точку для каждого из этих 329 наблюдений с координатами, указывающими на счет каждого наблюдения для этих двух основных компонентов в графике. Например, точки около левого края этого графика имеют самую низкую музыку к первому основному компоненту. Точки масштабируются относительно максимального значения счета и максимальной содействующей длины, поэтому только их относительные местоположения могут быть определены из графика.

Можно идентифицировать элементы в графике путем выбора Tools> Data Cursor в окне рисунка. Путем нажатия на переменную (вектор) можно считать переменную метку и коэффициенты для каждого основного компонента. Путем нажатия на наблюдение (точка) можно считать имя наблюдения и музыку к каждому основному компоненту. Можно задать 'Obslabels',names, чтобы показать имена наблюдения вместо чисел наблюдения в отображении Data Cursor.

Создайте 3D bi-график.

Можно также сделать bi-график в трех измерениях.

figure()
biplot(coefforth(:,1:3),'Scores',score(:,1:3),'Obslabels',names);
axis([-.26 0.8 -.51 .51 -.61 .81]);
view([30 40]);

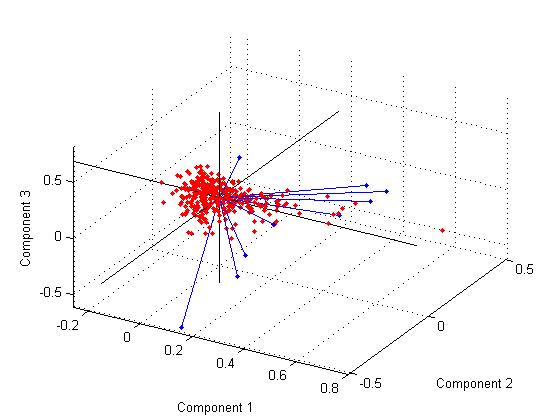
Этот график полезен, если первые две основных координаты не объясняют достаточно отклонения в ваших данных. Можно также вращать фигуру, чтобы видеть его от различных углов путем выбора theTools> Rotate 3D.