Регрессия с категориальными ковариантами

Этот пример показывает, как выполнить регрессию с категориальными ковариантами с помощью категориальных массивов и fitlm.

Загрузка демонстрационных данных.

load carsmall

Переменная MPG содержит измерения на милях на галлон 100 демонстрационных автомобилей. Модельный год каждого автомобиля находится в переменной Model_Year, и Weight содержит вес каждого автомобиля.

Отобразите сгруппированные данные на графике.

Чертите график рассеивания MPG против Weight, сгруппированного модельным годом.

figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
title('MPG vs. Weight, Grouped by Model Year')

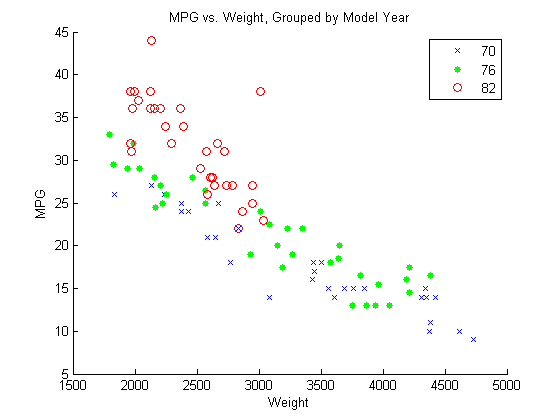
Группирующая переменная, Model_Year, имеет три уникальных значения, 70, 76 и 82, соответствуя модельным годам 1970, 1976, и 1982.

Составьте таблицу и категориальный массив.

Составьте таблицу, которая содержит переменные MPG, Weight и Model_Year. Преобразуйте переменную Model_Year в категориальный массив.

cars = table(MPG,Weight,Model_Year);
cars.Model_Year = categorical(cars.Model_Year);

Соответствуйте модели регрессии.

Соответствуйте модели регрессии использование fitlm с MPG как зависимая переменная, и Weight и Model_Year как независимые переменные. Поскольку Model_Year является категориальным ковариантом с тремя уровнями, он должен ввести модель как две переменные индикатора.

График рассеивания предполагает, что наклон MPG против Weight может отличаться в течение каждого модельного года. Чтобы оценить это, включайте периоды взаимодействия года веса.

Предложенная модель

$E (M P G) = β_{0} + β_{1} W e i g h t + β_{2} I [1976] + β_{3} I [1982] + β_{4} W e i g h t \times I [1976] + β_{5} W e i g h t \times I [1982],$

где I [1976] и I [1982] является фиктивными переменными, указывающими на модельные годы 1976 и 1982, соответственно. I [1976] принимает значение 1, если модельный год 1976 и принимает значение 0, если это не. I [1982] принимает значение 1, если модельный год 1982 и принимает значение 0, если это не. В этой модели, 1970 ссылочный год.

fit = fitlm(cars,'MPG~Weight*Model_Year')

fit = 


Linear regression model:
    MPG ~ 1 + Weight*Model_Year

Estimated Coefficients:
                             Estimate          SE    
                            ___________    __________

    (Intercept)                  37.399        2.1466
    Weight                   -0.0058437    0.00061765
    Model_Year_76                4.6903        2.8538
    Model_Year_82                21.051         4.157
    Weight:Model_Year_76    -0.00082009    0.00085468
    Weight:Model_Year_82     -0.0050551     0.0015636


                             tStat        pValue  
                            ________    __________

    (Intercept)               17.423    2.8607e-30
    Weight                   -9.4612    4.6077e-15
    Model_Year_76             1.6435       0.10384
    Model_Year_82             5.0641    2.2364e-06
    Weight:Model_Year_76    -0.95953       0.33992
    Weight:Model_Year_82     -3.2329     0.0017256


Number of observations: 94, Error degrees of freedom: 88
Root Mean Squared Error: 2.79
R-squared: 0.886,  Adjusted R-Squared: 0.88
F-statistic vs. constant model: 137, p-value = 5.79e-40

Регрессия вывод показывает:

fitlm распознает Model_Year категориальной переменной и создает необходимый индикатор (макет) переменные. По умолчанию первый уровень, 70, является ссылочной группой (используйте reordercats, чтобы изменить ссылочную группу).
Образцовая спецификация, MPG~Weight*Model_Year, задает условия первого порядка для Weight и Model_Year и всех взаимодействий.
Модель ^R2 = 0.886, означая изменение в милях на галлон уменьшается на 88,6%, когда вы рассматриваете вес, модельный год и их взаимодействия.

Подобранная модель

$M \hat{P} G = 37.4 - 0.006 W e i g h t + 4.7 I [1976] + 21.1 I [1982] - 0.0008 W e i g h t \times I [1976] - 0.005 W e i g h t \times I [1982] .$

Таким образом предполагаемые уравнения регрессии в течение модельных лет следующие.

Модельный год	Предсказанный MPG против веса
1970	$M \hat{P} G = 37.4 - 0.006 W e i g h t$
1976	$M \hat{P} G = (37.4 + 4.7) - (0.006 + 0.0008) W e i g h t$
1982	$M \hat{P} G = (37.4 + 21.1) - (0.006 + 0.005) W e i g h t$

Модельный год

Предсказанный MPG против веса

1970

$M \hat{P} G = 37.4 - 0.006 W e i g h t$

1976

$M \hat{P} G = (37.4 + 4.7) - (0.006 + 0.0008) W e i g h t$

1982

$M \hat{P} G = (37.4 + 21.1) - (0.006 + 0.005) W e i g h t$

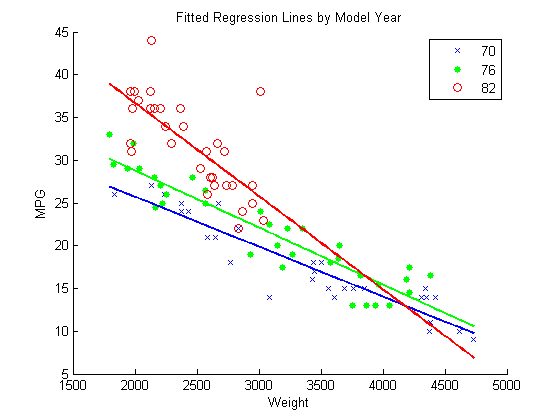
Отношение между MPG и Weight имеет все больше отрицательный наклон, когда модельный год увеличивается.

Постройте адаптированные линии регрессии.

Отобразите на графике данные и адаптированные линии регрессии.

w = linspace(min(Weight),max(Weight));

figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
line(w,feval(fit,w,'70'),'Color','b','LineWidth',2)
line(w,feval(fit,w,'76'),'Color','g','LineWidth',2)
line(w,feval(fit,w,'82'),'Color','r','LineWidth',2)
title('Fitted Regression Lines by Model Year')

Протестируйте на различные наклоны.

Протестируйте на существенные различия между наклонами. Это эквивалентно тестированию гипотезы

$\begin{array}{l} H_{0} : β_{4} = β_{5} = 0 \\ H_{A} : β_{i} \neq 0 для at least один i . \end{array}$

anova(fit)

ans = 

                         SumSq     DF    MeanSq    F         pValue    
    Weight               2050.2     1    2050.2    263.87    3.2055e-28
    Model_Year           807.69     2    403.84    51.976    1.2494e-15
    Weight:Model_Year    81.219     2    40.609    5.2266     0.0071637
    Error                683.74    88    7.7698

Этот вывод показывает, что p - значением для теста является 0.0072 (из строки взаимодействия, Weight:Model_Year), таким образом, нулевая гипотеза отклоняется на 0,05 уровнях значения. Значением тестовой статистической величины является 5.2266. Степенями свободы числителя для теста является 2, который является количеством коэффициентов в нулевой гипотезе.

Существуют достаточные доказательства, что наклоны не равны в течение всех трех модельных лет.

Документация