daetools:: reduceDAEIndexПреобразуйте систему дифференциальных алгебраических уравнений первого порядка к эквивалентной системе дифференциального индекса 1
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
[newEqs,newVars,R,oldIndex] := daetools::reduceDAEIndex(eqs,vars)
[newEqs,newVars,R,oldIndex] := daetools::reduceDAEIndex(eqs,vars) преобразовывает систему высокого индекса дифференциальных алгебраических уравнений первого порядка eqs к эквивалентной системе newEqs дифференциального индекса 1. Функция daetools::reduceDAEIndex сохраняет исходные уравнения и переменные и вводит новые переменные и уравнения. Это также возвращает матричный R, который выражает новые переменные в newVars как производные исходных переменных vars и дифференциального индекса oldIndex исходной системы ДАУ, eqs.
После преобразования daetools::reduceDAEIndex проверяет дифференциальный индекс новой системы путем вызова daetools::isLowIndexDAE. Если индексом newEqs является 2 или выше, то daetools::reduceDAEIndex выдает предупреждение.
Реализация daetools::reduceDAEIndex использует алгоритм Pantelides. Этот алгоритм уменьшает системы более высокого индекса до систем более низкого индекса путем выборочного добавления дифференцируемых форм исходных уравнений. Алгоритм Pantelides может недооценить дифференциальный индекс новой системы, и поэтому, может не уменьшать дифференциальный индекс до 1. В этом случае daetools::reduceDAEIndex выдает предупреждение и возвращает значение oldIndex как UNKNOWN. Использование функции daetools::reduceDAEToODE более надежное, но более медленное Исключение Гаусса. Обратите внимание на то, что daetools::reduceDAEToODE требует, чтобы система ДАУ была полулинейна.
Уменьшайте дифференциальный индекс системы, которая содержит два дифференциальных алгебраических уравнения второго порядка. Поскольку уравнения являются уравнениями второго порядка, сначала используйте reduceDifferentialOrder, чтобы переписать систему к системе ДАУ первого порядка.
Создайте следующую систему двух ДАУ второго порядка. Здесь, x(t), y(t) и F(t) являются переменными состояния системы.
eqs := [diff(x(t), t, t) = -F(t)*x(t),
diff(y(t), t, t) = -F(t)*y(t) - g,
x(t)^2 + y(t)^2 = r^2];
vars := [x(t), y(t), F(t)]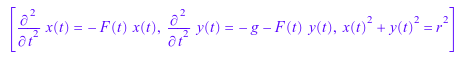
![]()
Перепишите эту систему так, чтобы все уравнения стали дифференциальными уравнениями первого порядка. Функция daetools::reduceDifferentialOrder заменяет ДАУ второго порядка по двум выражениям первого порядка путем представления новых переменных Dxt(t) и Dyt(t).
[eqs, vars, R] := daetools::reduceDifferentialOrder(eqs, vars): newEquations = eqs; newVariables = vars; relations = R

![]()
![]()
Используйте daetools::reduceDAEIndex, чтобы переписать систему так, чтобы дифференциальным индексом был 1.
[eqs,vars,R,originalIndex] := daetools::reduceDAEIndex(eqs,vars): newEquations = eqs; newVariables = vars; relations = R; originalDAEIndex = originalIndex

![]()
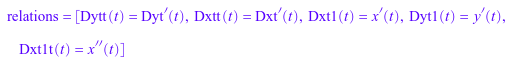
![]()
Используйте daetools::reduceRedundancies, чтобы сократить систему.
[eqs, vars, solvedEquations, constantVariables, replacedVariables, otherEquations] := daetools::reduceRedundancies(eqs, vars): newEquations = eqs; newVariables = vars;
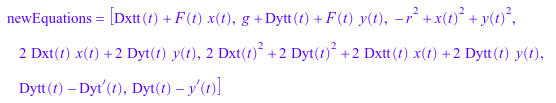
![]()
|
Список или вектор уравнений или выражений в переменных состояния |
|
Список или вектор идентификаторов или выражений, таких как |
Вложенный список, содержащий следующие четыре списка: список новых уравнений, список новых переменных, список отношений между новыми и исходными переменными и дифференциальный индекс исходной системы ДАУ. Если daetools::reduceDAEIndex не удается уменьшать дифференциальный индекс до 1, то это выдает предупреждение и возвращает UNKNOWN вместо дифференциального индекса исходной системы ДАУ.