daetools:: reduceDAEToODEПреобразуйте систему квазилинейных дифференциальных алгебраических уравнений первого порядка к эквивалентной системе дифференциального индекса 0
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
[newEqs,constraintEqs,oldIndex] = daetools::reduceDAEToODE(eqs,vars)
[newEqs,constraintEqs,oldIndex] := daetools::reduceDAEToODE(eqs,vars) преобразовывает систему высокого индекса полулинейных алгебраических уравнений первого порядка eqs к эквивалентной системе обыкновенных дифференциальных уравнений, newEqs. Это также возвращает вектор уравнений ограничений и дифференциального индекса oldIndex исходной системы полулинейных ДАУ, eqs.
Дифференциальным индексом новой системы является 0, то есть, якобиан newEqs относительно производных переменных в vars является обратимым.
Реализация daetools::reduceDAEToODE основана на Исключении Гаусса. Этот алгоритм более надежен, чем алгоритм Pantelides, используемый daetools::reduceDAEIndex, но это может быть намного медленнее.
Количество уравнений eqs должно совпасть с количеством переменных vars.
Проверяйте, имеет ли система ДАУ минимум (0 или 1) или высокий (>1) дифференциальный индекс. Если индекс выше, чем 1, то сначала пытаются уменьшать индекс при помощи daetools::reduceDAEIndex и затем при помощи daetools::reduceDAEToODE.
Создайте следующую систему дифференциальных алгебраических уравнений. Здесь, x1(t), x2(t) и x3(t) представляют переменные состояния системы. Система также содержит выражения q1(t), q2(t) и q3(t), которые не представляют переменные состояния.
eqs := [diff(x2(t),t) = q1(t) - x1(t),
diff(x3(t),t) = q2(t) - 2*x2(t) - t*(q1(t)-x1(t)),
q3(t) - t*x2(t) - x3(t) = 0];
vars := [x1(t), x2(t), x3(t)]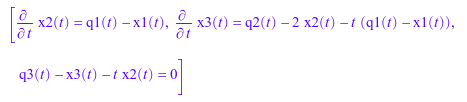
![]()
Используйте daetools::isLowIndexDAE, чтобы проверять дифференциальный индекс системы. Для этой системы daetools::isLowIndexDAE возвращает FALSE. Это означает, что дифференциальным индексом системы является 2 или выше.
daetools::isLowIndexDAE(eqs, vars)
![]()
Используйте daetools::reduceDAEIndex в качестве своей первой попытки переписать систему так, чтобы дифференциальным индексом был 1. Для этой системы daetools::reduceDAEIndex выдает предупреждение, потому что это не может уменьшать дифференциальный индекс системы к 0 или 1.
[newEqs, newVars, R, oldIndex] :=
daetools::reduceDAEIndex(eqs, vars):
newEquations = newEqs;
newVariables = newVars;
relations = R;
originalIndex = oldIndexWarning: Index of reduced DAEs is larger than 1. [daetools::reduceDAEIndex]
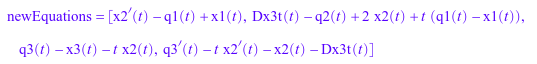
![]()
![]()
![]()
Если daetools::reduceDAEIndex не может уменьшать полулинейную систему так, чтобы индексом был 0 или 1, попытайтесь использовать daetools::reduceDAEToODE. Эта функция может быть намного медленнее, поэтому она не рекомендуется как предпочтительный вариант.
[newEqs, constraintEqs, oldIndex] :=
daetools::reduceDAEToODE(eqs, vars):
ODEs = eqs;
constraintEquations = constraintEqs;
originalIndex = oldIndex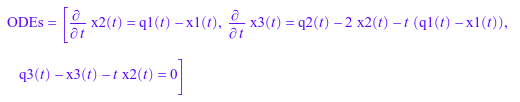
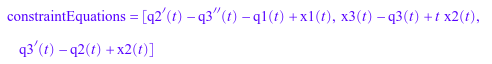
![]()
|
Список или вектор уравнений или выражений в переменных состояния |
|
Список или вектор идентификаторов или выражений, таких как |
Вложенный список, содержащий следующие три списка: список обыкновенных дифференциальных уравнений, список уравнений ограничений, с которыми сталкиваются во время системного сокращения и дифференциального индекса исходной системы ДАУ.