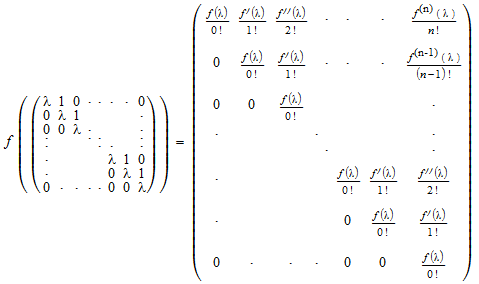Пример 1

Найдите матричный B, такой, что ^{B3 = A}, где A является 3х3 единичной матрицей.

Чтобы решить ^{B3 = A}, вычислите кубический корень матричного A с помощью функции funm. Создайте функцию, которая вычисляет кубический корень ее аргумента, и используйте его в качестве второго аргумента для funm. Кубический корень единичной матрицы является самой единичной матрицей.

A := matrix::identity(3):
f := x -> surd(x, 3)

funm(A, f)

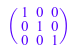
Замените один из элементов 0 матричного A с 1 и вычислите матричный кубический корень снова.

A[1, 2] := 1:
A

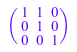
funm(A, f)

Теперь, вычислите кубический корень верхней треугольной матрицы.

A[1..2, 3] := [1, 1]:
A

B := funm(A, f)

Проверьте тот ^{B3 = A}.

B^3 = A

Пример 2

Найдите матрицу функцией Ламберта В.

Создайте 3х3 матрицу Паскаля A.

A := linalg::pascal(3)

Чтобы найти функцию Ламберта В (ответвление _W0) в матричном смысле, вызовите funm с помощью lambertW в качестве его второго аргумента. Аппроксимируйте результат с числами с плавающей запятой при помощи float.

W0 := funm(float(A), lambertW)

Проверьте, что этим результатом является решение матричного уравнения ^{A = W0·eW0} в текущей точности с плавающей точкой.

A = W0*exp(W0)

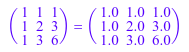
Теперь, найдите ответвление _W-1 функции Ламберта В для матричного A. Создайте функциональный f, представляющий ответвление _W-1 функции Ламберта В.

f := x -> lambertW(-1, x)

Вызовите funm с помощью f в качестве его второго аргумента. Аппроксимируйте результат с числами с плавающей запятой при помощи float.

Wm1 := funm(float(A), f)

Проверьте, что этим результатом является решение матричного уравнения ^{A = Wm1·eWm1} в текущей точности с плавающей точкой.

A = Wm1*exp(Wm1)

Возвращаемые значения

Массив, hfarray, или матрица.

Алгоритмы

Предположим f(x), где x является скаляром, имеет расширение Ряда Тейлора. Затем матричный функциональный f(A), где A является матрицей, задан Рядом Тейлора f(A) со сложением и умножением, выполняемым в матричном смысле.

Если A может быть представлен как ^{A = P·D·P-1}, где D является диагональной матрицей, такой что

затем матричный функциональный f(A) может быть вычислен можно следующим образом:

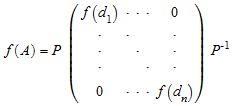
Недиагонализируемые матрицы могут быть представлены как ^{A = P·J·P-1}, где J является Жорданова форма матричного A. (Для получения дополнительной информации смотрите linalg::jordanForm.) Затем матричный функциональный f(A) может быть вычислен при помощи следующего определения на каждом Иорданском блоке: