intersect, _intersectПересечение множеств или интервалы или оба
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
set1 intersect set2
_intersect(set1, set2, …)
intersect вычисляет пересечение множеств и интервалы.
set1 intersect set2 эквивалентен _intersect(set1, set2).
Приоритеты intersect, minus, union следующие. Если в сомнении, используйте круглые скобки, чтобы гарантировать, что выражение анализируется, как желаемый.
Оператор intersect является более сильной привязкой, чем minus, то есть, set1 intersect set2 minus set3 = (set 1 intersect set2) minus set3.
Оператор minus является более сильной привязкой, чем union, то есть, set1 minus set2 union set3 = (set1 minus set2) union set3.
set1 minus set2 minus set3 = (set 1 minus set2) minus set3
Если наборы или интервалы заданы символьными выражениями включающие идентификаторы или индексируемые идентификаторы, то на символьные звонки _intersect отвечают. На экране они представлены через обозначение оператора set1 intersect set2.
На конечных множествах типа DOM_SET intersect действует чисто синтаксическим способом. Например, {1} intersect {x} упрощает до пустого множества {}. Математически, этот результат может быть неправильным в целом, потому что x может представлять значение 1.
На интервалах типа Dom::Interval intersect действует семантическим способом. В частности, свойства идентификаторов учтены.
_intersect() возвращает universe (типа stdlib::Universe), который представляет набор всех математических объектов.
intersect работает с конечными множествами:
{x, 1, 5} intersect {x, 1, 3, 4}![]()
Для символьных наборов, заданных как идентификаторы или индексированные идентификаторы, отвечают на символьные звонки:
{1, 2} intersect A intersect {2, 3}![]()
Обратите внимание на то, что intersect действует на конечные множества чисто синтаксическим способом. В следующем вызове x не совпадает ни с одним из чисел 1, 2, 3 синтаксически:
{1, 2, 3} intersect {1, x}![]()
intersect перегружается доменным Dom::Interval:
Dom::Interval(2, infinity) intersect Dom::Interval([1, 3])
![]()
{PI/2, 2, 2.5, 3} intersect Dom::Interval(1,3)![]()
В отличие от конечных множеств типа DOM_SET, область интервала работает семантически. Это принимает во внимание properties:
Dom::Interval(-1, 1) intersect {x}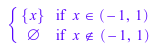
assume(0 < x < 1):
Dom::Interval(-1, 1) intersect {x}![]()
unassume(x):
Следующий список обеспечивает набор наборов:
L := [{a, b}, {1, 2, a, c}, {3, a, b}, {a, c}]:Функциональный эквивалент _intersect оператора intersect принимает произвольное число аргументов. Таким образом пересечение всех наборов в L может быть вычислено можно следующим образом:
_intersect(op(L))
![]()
delete L:
|
Конечные множества типа |
Установите, интервал, символьное выражение типа "_intersect" или universe.
set1, set2