lambertWФункция Ламберта
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
lambertW(x) lambertW(k,x)
Для целочисленного k значения
представляют решения уравнения y ey = x.
lambertW является обратной функцией
.
В комплексной плоскости уравнение y ey = x имеет исчисляемо бесконечное число решений. Они представлены lambertW(k, x) с k, передвигающимся на целые числа.
Для всего действительного x ≥ 0, уравнение
имеет точно одно действительное решение. Это представлено y=lambertW(x) или, эквивалентно, y=lambertW(0, x).
Для всего действительного x в области значений-exp (-1) <x <0, существует точно два действительных решения. Больший представлен y=lambertW(x), меньшим y=lambertW(-1, x).
Точно одно действительное решение lambertW(0, -exp(-1))= lambertW(-1, -exp(-1))= -1 существует для
.
Поскольку, lambertW(k, x) не принимает никакое действительное значение.
Значения lambertW(-1, 0)=- infinity и lambertW(0, 0)=0 реализованы. Далее, результат y возвращен для некоторых точных аргументов формы
. Для аргументов с плавающей точкой возвращено значение с плавающей точкой. Для всех других аргументов возвращены неоцененные вызовы функции.
Атрибуты float являются функциями ядра, т.е. оценка с плавающей точкой быстра.
Когда названо аргументом с плавающей точкой, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
lambertW(-3), lambertW(-1, -5/2), lambertW(1/2), lambertW(5, I), lambertW(3, 1 + I), lambertW(-1, x + 1)
Некоторые точные значения найдены:
lambertW(-1, -exp(-1)), lambertW(-1, -2*exp(-2)), lambertW(-1, -3/2*exp(-3/2)), lambertW(exp(1)), lambertW(2*exp(2)), lambertW(5/2*exp(5/2)), lambertW(1, (3+4*I)*exp(3+4*I))
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
lambertW(-1, -0.3), lambertW(2000.0)
lambertW(-3, -0.277), lambertW(1, 2345.6)
Функции diff, float и series обрабатывают выражения, включающие функцию Ламберта:
diff(lambertW(k, x), x)
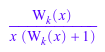
float(ln(3 + lambertW(sqrt(PI))))
series(lambertW(x), x = 0); series(lambertW(x), x = -1/exp(1), 3); series(lambertW(-1, x), x = -1/exp(1), 3);
|
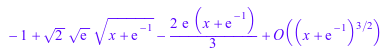
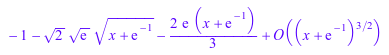
Арифметическое выражение, “аргумент” |
|
Арифметическое выражение, представляющее целое число, “ответвление” |
Арифметическое выражение.
Р.М. Корлесс, Д.Дж. Джеффри и Д. Нут: “Последовательность Ряда для Функции Ламберта В”, в: Продолжения ISSAC '97, Мауи, Гавайи. В.В. Куечлин (редактор).. Нью-Йорк: ACM, стр 197-204, 1997.