diffДифференцируйте выражение или полином
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
diff(f) diff(f,x) diff(f, x1, x2, …)
diff(f, x) вычисляет производную![]() функционального
функционального f относительно переменной x.
diff(f, x) вычисляет частную производную арифметического выражения (или полином) f относительно неопределенного x.
diff(f) вычисляет 0th производную f. Поскольку 0th производной f является сам f, diff(f) возвращает свой оцененный аргумент.
diff(f, x1, x2, ...) эквивалентен diff(...diff(diff(f, x1), x2)...). В обоих случаях MuPAD® сначала дифференцирует f относительно x1, затем дифференцирует результат относительно x2 и так далее. Результатом является частная производная![]() . Смотрите Пример 2.
. Смотрите Пример 2.
Если вы используете, вложил вызовы diff, система внутренне преобразовывает их в один вызов diff с несколькими аргументами. Смотрите Пример 3.
При вычислении вторых и производных высшего порядка используйте оператор последовательности в качестве ярлыка. Если n является неотрицательным целым числом, diff(f, x $ n) возвращает n th производная f относительно x. Смотрите Пример 4.
indeterminates x, x1, x2, ... должен быть идентификаторами доменного типа DOM_IDENT или индексированные идентификаторы формы x[n], где x является идентификатором, и n является целым числом. Если кто-либо неопределенный приезжает в какую-либо другую форму, MuPAD отвечает на неразрешенный звонок diff. Смотрите Пример 5.
Если f является арифметическим выражением, diff возвращает арифметическое выражение. Если f является полиномом, diff возвращает полином. Смотрите Пример 6.
Если система не может вычислить производную, она отвечает на неразрешенный звонок diff. Смотрите Пример 7.
MuPAD принимает, что частные производные относительно различного indeterminates коммутируются. Вызовы функции diff(f, x1, x2) и diff(f, x2, x1) приводят к тому же результату diff(f, y1, y2). Здесь [y1, y2] = sort([x1, x2]). Смотрите Пример 8.
MuPAD обеспечивает две функции, diff и D, для вычислительных производных. Используйте дифференциальный оператор D, чтобы вычислить производные функций. Используйте функцию diff, чтобы вычислить производные арифметических выражений. Математически, D(f)(x) совпадает с diff(f(x), x), и D([1, 2], f)(x, y) совпадает с diff(f(x, y), x, y). Можно преобразовать символьные вызовы D к вызовам diff и наоборот при помощи rewrite. Смотрите Пример 10.
Можно расширить функциональность diff для собственных специальных математических функций через перегрузку. Этот подход работает путем превращения соответствующей функции в функциональную среду и реализации правила дифференцирования для функции как slot "diff" функциональной среды.
Если подвыражение формы, g(..) происходит в f и g, является функциональной средой, то diff(f, x) пытается вызвать слот "diff" g, чтобы определить производную g(..).
Системные вызовы слот "diff" с аргументами g(..), x.
Если g не имеет слота "diff", то системная функция diff возвращает символьное выражение diff(g(..), x) для производной подвыражения.
Система всегда вызывает слот "diff" точно с двумя аргументами. Если вы вызываете функцию diff с большим количеством indeterminates (например, если вы вычисляете производную высшего порядка), то MuPAD несколько раз вызывает слот "diff". Каждый вызов вычисляет производную относительно одного неопределенного. Система кэширует результаты вызовов слотов "diff" в diff в порядке предотвратить избыточные вызовы функции. Смотрите Пример 11.
Точно так же, если элемент d области библиотеки, T происходит как подвыражение f, то diff(f, x) вызывает слот T::diff(d, x), чтобы вычислить производную d.
Если доменный T не имеет слота "diff", то diff рассматривает этот объект как константу и возвращается 0 для соответствующего подвыражения.
Если вы дифференцируете выражение или функцию, содержащую abs или sign, гарантируете, что аргументы являются действительными значениями. Для сложных аргументов abs и sign, функция diff официально вычисляет производную, но этот результат не обычно допустим, потому что abs и sign не дифференцируемы по комплексным числам.
Вычислите производную x 2 относительно x:
diff(x^2, x)
![]()
Можно дифференцироваться относительно нескольких переменных в одном вызове diff. Например, дифференцируйте это выражение относительно x, и затем с дифференцируют результат относительно y:
diff(x^2*sin(y), x, y) = diff(diff(x^2*sin(y), x), y)
![]()
MuPAD внутренне преобразовывает, вложил вызовы diff в один вызов diff с несколькими аргументами:
diff(diff(f(x, y), x), y)
![]()
Используйте оператор последовательности $ в качестве ярлыка, чтобы вычислить третью производную этого выражения относительно x:
diff(sin(x)*cos(x), x $ 3)
![]()
Можно дифференцироваться относительно индексируемого идентификатора. Например, дифференцируйте это выражение относительно x[1]:
diff(x[1]*y + x[1]*x[r], x[1])
![]()
Можно дифференцировать polynomials относительно полинома indeterminates или параметров в коэффициентах. Например, дифференцируйте этот полином относительно неопределенного x:
diff(poly(sin(a)*x^3 + 2*x, [x]), x)
![]()
Теперь дифференцируйте тот же полином относительно его символьного параметра a:
diff(poly(sin(a)*x^3 + 2*x, [x]), a)
![]()
MuPAD возвращает производную неизвестной функции как неразрешенный вызов diff:
diff(f(x) + x, x)
![]()
MuPAD принимает, что все частные производные относительно различного indeterminates коммутируются. Поэтому система может изменить порядок indeterminates:
diff(f(x, y), x, y) = diff(f(x, y), y, x);
![]()
Можно использовать diff, чтобы дифференцировать символьные интегралы. Например, вычислите вторую производную этого неопределенного интеграла:
F1 := int(f(x), x): diff(F1, x, x)
![]()
Теперь вычислите производную определенного интеграла:
F2 := int(f(t, x), t = x..x^2): diff(F2, x)
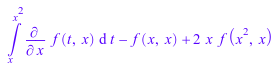
Используйте оператор D, чтобы вычислить производные функций. Используйте функцию diff, чтобы вычислить производные выражений:
D(sin), diff(sin(x), x)
![]()
Применение D к выражениям и diff к функциям не имеет никакого смысла:
D(sin(x)), diff(sin, x)
![]()
Используйте функцию rewrite, чтобы переписать выражение, заменяющее оператор D на функцию diff:
rewrite(D(f)(x), diff), rewrite(D(D(f))(x), diff)
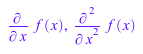
Кроме того, используйте rewrite, чтобы переписать выражение, заменяющее diff на D:
diff(f(x, x), x) = rewrite(diff(f(x, x), x), D)
![]()
Можно расширить diff к собственным специальным функциям. Для этого встройте свою функцию, f, в функциональную среду, g, и реализуйте поведение diff для этой функции как слот "diff" функциональной среды.
Если подвыражение формы, g(..) происходит в выражении f, то diff(f, x) вызывает g::diff(g(..), x), чтобы определить производную подвыражения g(..).
Этот пример демонстрирует расширение diff показательной функции. Начиная с функциональной среды exp уже имеет слот "diff", вызовите новую функциональную среду Exp, чтобы не перезаписывать существующую системную функцию exp.
Здесь, слот "diff" реализует цепочечное правило для показательной функции. Производная является продуктом исходного вызова функции и производной аргумента:
Exp := funcenv(Exp): Exp::diff := proc(f, x) begin // f = Exp(something), i.e., something = op(f, 1) f*diff(op(f, 1), x): end_proc: diff(Exp(x^2), x)
![]()
Отчет, созданный prog::trace, показывает один вызов Exp::diff с двумя аргументами. Вместо того, чтобы вызвать Exp::diff дважды, система читает необходимый результат второго вызова из внутреннего кэша для промежуточных результатов в diff:
prog::trace(Exp::diff): diff(Exp(x^2), x, x)
enter Exp::diff(Exp(x^2), x) computed 2*x*Exp(x^2)
![]()
prog::untrace(Exp::diff): delete f, Exp:
|
Арифметическое выражение или полином типа |
|
Indeterminates: идентификаторы или индексированные идентификаторы |
f