linalg:: isUnitaryПротестируйте, унитарна ли матрица
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::isUnitary(A)
linalg::isUnitary тестирует, является ли матричный A унитарной матрицей. n ×n матричный A унитарен, если![]() , где I n является n ×n единичная матрица.
, где I n является n ×n единичная матрица.
A квадратной матрицы является унитарной матрицей, если и только если столбцы A формируют ортонормированный базис относительно скалярного произведения linalg::scalarProduct двух векторов.
Правильность результата, который может только быть гарантирован FALSE linalg::isUnitary, если элементы кольцевого R компонента матричного A будут канонически представлены, т.е. если каждый элемент R имеет только одно уникальное представление.
Ax::canonicalRep аксиомы утверждает, что область имеет это свойство. Следовательно, linalg::isUnitary возвращает FALSE или UNKNOWN, соответственно, в зависимости от того, имеет ли звонок компонента A аксиому Ax::canonicalRep.
Если звонок компонента A не задает метод "conjugate" затем, это проверяется, является ли A ортогональной матрицей, таким образом, что A At = E n, где E n является n ×n единичная матрица.
Следующая матрица унитарна:
A := 1/sqrt(5) * matrix([[1, 2], [2, -1]])
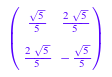
linalg::isUnitary(A)
![]()
|
Квадратная матрица области категории |
Или TRUE, FALSE или UNKNOWN.