Взаимодействия среды

Свойства идентификаторов учтены.

Пример 1

Мы вычисляем скалярное произведение векторов (i, 1) и (1, - i):

MatC := Dom::Matrix(Dom::Complex):
u := MatC([I, 1]): v := MatC([1, -I]):
linalg::scalarProduct(u, v)

Пример 2

Мы вычисляем скалярное произведение векторов и с символьными записями u ₁, u ₂, v ₁, v ₂ по стандартному звонку компонента для матриц:

delete u1, u2, v1, v2:
u := matrix([u1, u2]): v := matrix([v1, v2]):
linalg::scalarProduct(u, v)

Можно использовать assume, чтобы сказать системе, что символьные компоненты должны представлять вещественные числа:

assume([u1, u2, v1, v2], Type::Real):

Затем скалярное произведение и упрощает до:

linalg::scalarProduct(u, v)

Также опция Real может быть задана:

unassume(u1, u2, v1, v2):
linalg::scalarProduct(u, v, Real)

Пример 3

Одно конкретное скалярное произведение в вещественном векторном пространстве непрерывных функций на интервале [0, 1] задано

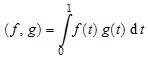Чтобы вычислить ортогональное основание, соответствующее полиномиальному основанию 1, t, t ², t ³, … относительно этого скалярного произведения, мы заменяем стандартное скалярное произведение следующей процедурой:

standardScalarProduct := linalg::scalarProduct:
unprotect(linalg):
linalg::scalarProduct := proc(u, v) 
    local F, f, t;
begin
    // (0)
    f := expr(u[1] * v[1]);

     // (1)
    t := indets(f);
    if t = {} then t := genident("t") else t := op(t, 1) end_if;

     // (2)
    F := int(f, t = 0..1);

     // (3)
    u::dom::coeffRing::coerce(F)
end:

Мы запускаем с шага (0), чтобы преобразовать f (t)  g (t) к выражению основного доменного типа, такого, что системная функция int на шаге, (2) может обработать свой вход (это не необходимо, если элементы звонка компонента векторов уже представлены элементами основных областей).

Шаг (1) извлекает неопределенные из полиномов, шаг (2), вычисляет скалярное произведение, как задано выше и шаг, (3) преобразовывает результат назад в элемент звонка компонента векторов u и v.

Обратите внимание на то, что мы должны оставить идентификатор, защищенный от записи без защиты, linalg, в противном случае присвоение привело бы к сообщению об ошибке.

Мы затем создаем матрицу, которая состоит из первых пяти из вышеупомянутых полиномов:

P := matrix([[1, t, t^2, t^3, t^4]])

Если мы теперь выполняем процедуру Ортогонализации Грама-Шмидта на столбцах P с функциональным linalg::orthog, мы добираемся:

S := linalg::orthog(linalg::col(P, 1..4))

Каждый вектор в S является ортогональным к другим векторам в S относительно измененного скалярного произведения. Мы проверяем это на первый вектор:

linalg::scalarProduct(S[1], S[j]) $ j = 2..nops(S)

Наконец, мы отменяем переопределение скалярного произведения, чтобы не столкнуться с проблемой с последующими вычислениями:

linalg::scalarProduct := standardScalarProduct:
protect(linalg, Error):

Возвращаемые значения

Элемент звонка компонента u и v.