linalg:: wiedemann
Решение линейных систем алгоритмом Видемана
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
linalg::wiedemann(A, b, <mult>, <prob>)
Описание
linalg::wiedemann(A, b, mult, ...) пытается найти вектор
, который удовлетворяет уравнению
при помощи алгоритма Видемана.
mult параметра должен быть функцией, таким образом, что результат mult(A,y) равняется
для каждого n - размерный вектор-столбец
. Параметр y имеет тот же доменный тип как A. Аргумент mult не должен обрабатывать другие типы параметров, и при этом он не должен обрабатывать другие матрицы, чем A.
linalg::wiedemann использует вероятностный алгоритм. Поскольку детерминированный вариант вводит FALSE для дополнительного параметра prob.
Если система
не имеет решения, то linalg::wiedemann возвращает FAIL.
Если система
имеет больше чем одно решение, то случайный возвращен.
Из-за вероятностной природы алгоритма Видемана, вычисление может перестать работать с маленькой вероятностью. В этом случае возвращен FAIL. Если детерминированный вариант выбран, то алгоритм может быть медленнее для небольшого количества матриц.
Векторный b должен быть задан по звонку компонента A.
Содействующий звонок A должен быть полем, т.е. областью категории Cat::Field.
Рекомендуется использовать linalg::wiedemann, только если mult использует значительно меньше, чем O (n 2) деятельность на местах.
Примеры
Пример 1
Мы задаем матрицу и вектор-столбец по конечному полю с 29 элементами:
MatZ29 := Dom::Matrix(Dom::IntegerMod(29)): A := MatZ29([[1, 2, 3], [4, 7, 8], [9, 12, 17]]); b := MatZ29([1, 2, 3])
Поскольку A не имеет специальной формы, которая позволила бы быстрое матричное векторное умножение, мы просто используем _mult. Алгоритм Видемана работает в этом случае, несмотря на то, что это менее эффективно, чем Исключение Гаусса:
linalg::wiedemann(A, b, _mult)
Пример 2
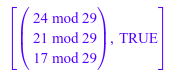
Теперь давайте зададим другую матрицу, которая имеет специальную форму:
MatZ29 := Dom::Matrix(Dom::IntegerMod(29)): A := MatZ29([[1, 0, 0], [0, 1, 2], [0, 0, 1]]); b := MatZ29(3, 1, [1, 2, 3]):
Для этой конкретной матрицы легко задать эффективный метод умножения:
mult := proc(dummy, y)
begin
y[2]:=y[2]+2*y[3];
y
end:
linalg::wiedemann(A, b, mult)
Параметры
|
n ×n матрица области категории |
|
n - размерный вектор-столбец, т.е. n ×1 матрица области категории |
|
Метод матричного векторного умножения: функционируйте или функциональное выражение; значение по умолчанию: |
|
|
Возвращаемые значения
Или список [x, TRUE], если решение для системы
было найдено, или список [x, FALSE], если ненулевое решение для соответствующей гомогенной системы
было найдено, или значение FAIL (см. ниже).
Алгоритмы
Ожидаемым временем выполнения для вероятностного алгоритма является O (n 2 + n M), и временем выполнения для детерминированного варианта является O (n 2 M) в худшем случае, но только O (n 2 + n M) в среднем. Здесь, M является количеством деятельности на местах, которую использует стандартная программа матричного векторного умножения mult.
Основная идея об алгоритме состоит в том, чтобы решить линейную систему
путем нахождения минимального полиномиального f (y), который решает
. Если постоянный коэффициент c = f (0) является ненулевым и g (y): = f (y) - c, равенство
подразумевает, что это
- решение.
Полиномиальный f найден путем поиска минимального полиномиального h, удовлетворяющего
для некоторого случайным образом выбранного вектора - строки
. Это может привести к h ≠ f в неудачных случаях, но в целом вероятность для этого является маленькой.
Ссылки
[1] Дуглас Видеман: “Решая Разреженные Линейные уравнения по Конечным Полям”, Транзакции IEEE на Теории информации, издании 32, № 1, январь 1986.