linalg:: vandermondeSolveРешите линейную систему Вандермонда
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::vandermondeSolve(v, y, <Transposed>)
linalg::vandermondeSolve(v, y) возвращает решение
линейной системы Вандермонда
с i = 1, …, n.
linalg::vandermondeSolve использует O (n 2) элементарные операции, чтобы решить систему Вандермонда. Это быстрее, чем общий решатель solve и линейные решатели linsolve, numeric::linsolve, linalg::matlinsolve и numeric::matlinsolve.
Решение
, возвращенное linalg::vandermondeSolve([v[i] $ i=1..n], [y[i] $ i=1..n]), приводит к коэффициентам полиномиального p (v) = x 1 + x 2 v + ··· + x n vn - 1 интерполяция таблицы данных (v 1, y 1), …, (v n, y n), т.е.
.
Смотрите пример 1.
Вандермонд указывает v и правую сторону, y линейной системы вводится как векторы:
delete y0, y1, y2: v := matrix([[0, 1, 2]]); y := matrix([[y0, y1, y2]])
Вектор решения:
x := linalg::vandermondeSolve(v, y)
Решение приводит к коэффициентам интерполяционного многочлена:
P := v -> _plus(x[i+1]*v^i $ i=0..2):
через точки (0, y 0), (1, y 1), (2, y 2):
P(v[1]), P(v[2]), P(v[3])
С дополнительным аргументом Transposed решена линейная система с транспонированной матрицей Вандермонда, соответствующей v:
linalg::vandermondeSolve(v, y, Transposed)
delete v, y, x, P:
Вандермонд указывает v и правую сторону, y линейной системы вводится как 2×1 матрицы:
Mat := Dom::Matrix(Dom::ExpressionField(normal)):
delete v1, v2, y1, y2: v := Mat([v1, v2]): y := Mat([y1, y2]):
Мы задаем векторы по доменному Dom::ExpressionField (normal) в порядке упростить промежуточные вычисления.
Затем, мы вычисляем решение соответствующей системы Вандермонда:
x := linalg::vandermondeSolve(v, y)
Мы создаем матричный V Вандермонда и проверяем результат:
V := Mat([[1, v[1]], [1, v[2]]])
V * x
delete Mat, v, y, x, V:
Мы решаем систему Вандермонда по полю ℤ 7 (целые числа по модулю 7) представленный доменным Dom::IntegerMod (7):
MatZ7 := Dom::Matrix(Dom::IntegerMod(7)): v := MatZ7([1, 2, 3]): y := MatZ7([0, 1, 2]):
linalg::vandermondeSolve(v, y)
delete MatZ7, v, y:
|
Вектор с отличными элементами (вектором является n ×1 или 1 ×n матрица категории |
|
Вектор той же размерности и области вводит как |
|
Возвращает решение |
Вектор того же доменного типа как y.
Матрица Вандермонда
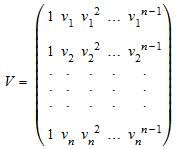
сгенерированный v = [v 1, …, v n] является обратимым, если и только если i v отличен.
Вектор
, возвращенный linalg::vandermondeSolve(x, y), является уникальным решением
.
Векторный x, возвращенный linalg::vandermondeSolve(x, y, Transposed), является уникальным решением
.
