Пример 1

Решите линейную систему:

по реалам. Во-первых, введите матрицу коэффициентов и правую сторону:

MatR := Dom::Matrix(Dom::Real):
A := MatR([[1, 2], [-1, 2]]); b := MatR([1, -1])

Затем, вызовите linalg::matlinsolve, чтобы решить систему:

x := linalg::matlinsolve(A, b)

Система имеет точно одно решение. Векторный x удовлетворяет матричному уравнению, данному выше:

A * x

Пример 2

Система:

не имеет решения по ℝ (на самом деле, ни по какой области компонента):

MatR := Dom::Matrix(Dom::Real):
A := MatR([[1, 2], [-1, -2]]): b := MatR([1, 0]):
linalg::matlinsolve(A, b)

Пример 3

Решите линейную систему:

по рациональным числам. Во-первых, введите матрицу коэффициентов и правую сторону:

MatQ := Dom::Matrix(Dom::Rational):
A := MatQ([[1, 1, -4, -7, -6], [0, 1, -3, -5, -7]]);
b := MatQ([30, 17])

Затем, вызовите linalg::matlinsolve, чтобы решить систему:

sol:= linalg::matlinsolve(A, b)

Результат состоит в том, чтобы быть интерпретирован можно следующим образом: первый вектор списка sol является конкретным решением линейной системы:

A * sol[1]

Вторая запись списка содержит базис для ядра A, т.е. пробел решения соответствующей однородной системы (ядро A). Возвращенное основание дано как список векторов.

Следующий вход проверяет этот факт путем вычисления продукта для каждого вектора списка sol[2]:

map(sol[2], x -> A * x)

Любое решение линейной системы может быть представлено как сумма конкретного решения (здесь: sol[1]) и линейная комбинация базисных векторов ядра A. Следовательно входная система имеет бесконечное число решений.

Например, другим решением системы дают:

x := sol[1] + 1*sol[2][1] + 1/2*sol[2][2] - 2*sol[2][3]

A * x

Если вы идентифицируете столбцы матрицы коэффициентов A линейной системы с переменными x ₁, x ₂, x ₃, x ₄, x ₅, то вы видите из общего решения что переменные x ₃, x ₄, x ₅ действий как свободные параметры. Они могут быть присвоены произвольные рациональные значения, чтобы получить уникальное решение.

Путем предоставления списка значений для этих переменных как третий параметр к linalg::matlinsolve можно выбрать определенный вектор из набора всех решений линейной системы. Например, чтобы выбрать тот же векторный x, как выбрано в предыдущем входе, введите:

linalg::matlinsolve(A, b, [0, 0, 1, 1/2, -2])

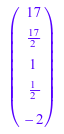
Если вы только интересуетесь конкретным решением и не нуждаетесь в общем решении линейной системы, введите:

linalg::matlinsolve(A, b, Special)

Этот вызов подавляет вычисление ядра A.

Пример 4

Если линейная система дана в форме уравнений, функциональный linalg::expr2Matrix может использоваться, чтобы сформировать соответствующее матричное уравнение:

delete x, y, z:
Ab := linalg::expr2Matrix(
  [x + y + z = 6, 2*x + y + 2*z = 10, x + 3*y + z = 10]
)

Результатом здесь является расширенная матрица коэффициентов входной системы, то есть, вектор правой стороны является 4-м вектор-столбцом матричного Ab. Поскольку вы не задавали звонок компонента для этой матрицы, стандартный звонок компонента для матриц, доменный Dom::ExpressionField (), был выбран.

Чтобы решить линейную систему, вызовите:

linalg::matlinsolve(Ab)

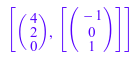
Система имеет бесконечное число решений. Третьи действия переменной z как свободный параметр и поэтому могут иметь любое (комплексное) значение.

Чтобы получить общее решение в форме параметра, можно использовать параметры для переменных x, y, z входной системы:

delete u, v, w:
sol := linalg::matlinsolve(Ab, [u, v, w])

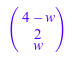
Это возможно здесь, потому что вы выполняете матричные вычисления по Dom::ExpressionField(), который позволяет вам вычислить с символическими (арифметическими) выражениями.

Выбрать определенный вектор из набора решений, например, решения для w = 1, введите:

x := subs(sol, w = 1)

Пример 5

Рассмотрите систему линейных уравнений с разреженной структурой, то есть, матрица коэффициентов имеет много нулевых компонентов:

eqs := {x1 + x5 = 0, x2 - x4 = 1, x3 + 2*x5 = 2, x4 - x5 = -1}:
Ab := linalg::expr2Matrix(eqs, [x1, x2, x3, x4, x5])

linalg::matlinsolve использует разреженность матрицы коэффициентов, если это передается как матрица типа Dom::Matrix. Также можно использовать функциональный linsolve, который позволяет разреженный ввод и вывод через символьные уравнения:

linsolve(eqs)

Также можно использовать функциональный numeric::matlinsolve с опцией Symbolic вместо linalg::matlinsolve:

A := linalg::delCol(Ab, 6):
b := linalg::col(Ab, 6):
numeric::matlinsolve(A, b, Symbolic)

Обратите внимание на то, что функциональный numeric::matlinsolve всегда перерабатывает подполе комплексных чисел и не позволяет вам задать область вычисления. Без опции Symbolic numeric::matlinsolve преобразовывает входные данные в числа с плавающей запятой.

Пример 6

Проверяйте ли матричное уравнение

имеет уникальное решение по целым числам.

Запустите путем ввода матрицы коэффициентов и матрицы правой стороны:

MatZ := Dom::Matrix(Dom::Integer):
A := MatZ([[1, 2], [-2, 3]]); B := MatZ([[4, 2], [6, 3]])

Затем, решите матричное уравнение:

X := linalg::matlinsolve(A, B)

Уравнение действительно имеет уникальное решение (в противном случае, ответ linalg::matlinsolve был бы пустым списком []). Проверяйте результат:

A * X

Пример 7

Если вы используете опцию Normal, linalg::matlinsolve вызывает функцию normal для конечных результатов. Этот вызов гарантирует, что linalg::matlinsolve возвращает результаты в нормированной форме:

A := matrix([[1, s], [t, -1]]):
b := matrix([s + 1, t - 1]):
x := linalg::matlinsolve(A, b)

Если вы задаете Normal = FALSE, linalg::matlinsolve не вызывает normal для конечного результата:

x := linalg::matlinsolve(A, b, Normal = FALSE)

Пример 8

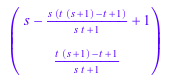
Решите эту систему:

A := matrix([[1, s], [1, t]]):
b := matrix([1, 1]):

linalg::matlinsolve(A, b)

Обратите внимание на то, что больше решений существует для t = s. linalg::matlinsolve не использует эти решения, потому что он делает некоторые дополнительные предположения на символьных параметрах этой системы. Чтобы видеть предположения что linalg::matlinsolve, сделанный при решении этой системы, используйте опцию ShowAssumptions:

linalg::matlinsolve(A, b, ShowAssumptions)

Возвращаемые значения

Без ShowAssumptions linalg::matlinsolve может возвратить вектор или список [S, KernelBasis] (возможно пустой), где S является вектором решения, и KernelBasis является списком базисных векторов для ядра A. Это также может возвратить матрицу или значение NIL.

Матрица и векторы, соответственно, имеют доменный тип Dom::Matrix(R), где R является звонком компонента A.

С ShowAssumptions linalg::matlinsolve возвращает список [S, KernelBasis, Constraints, Pivots]. Списки Constraints и Pivots содержат уравнения и неравенства, вовлекающие символьные параметры в A и b (или B). Внутренне, они были приняты, чтобы сохраняться при решении системы. Если система не разрешима, linalg::matlinsolve с ShowAssumptions возвращает [[], [], [], []].