график::Системы Lindenmayer
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Lsys(alpha, start, trans, …, <a = amin .. amax>, options)
plot::Lsys создает системы Lindenmayer, т.е. строку, переписывая системы, управляющие графикой с относительными командами.
Системы Lindenmayer или L-системы для краткости основаны на концепции итеративного преобразования строки символов в другую строку. После конечного числа итераций получившая строка переводится в последовательность команд перемещения “черепахе” (см. plot::Turtle), который может чертиться на экране.
В plot::Lsys строка символов представлена строкой символов, т.е. DOM_STRING. Правила преобразования даны как уравнения, сопоставляющие строки длины 1 к строкам произвольной длины. Правила черепахи даны как уравнения, сопоставляющие строки длины 1 к простым командам перемещения: Line, Move, Left, Right, Push, Pop, Noop или спецификация цветов.
Команды в основном очевидны. Left и Right поворачиваются суммой, установленной в слоте "RotationAngle"; начальное направление произошло. Line и Move перемещаются набором суммы в "StepLength", где Move не чертит линию. Push хранит текущее состояние (положение, направление, цвет) на стеке от того, где это может позже быть повторно активировано с помощью Pop. средние значения Noop “игнорируют это, никакая операция”. Спецификация цветов изменяет цвет линии.
Следующие правила черепахи использованы по умолчанию (но может быть отключен путем предоставления других правил для левых сторон):
"F" = Line, "f" = Move, "[" = Push, "]" = Pop, "+" = Left, "-" = Right.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
AntiAliased | сглаженные строки и точки? | FALSE |
Color | основной цвет | RGB::Blue |
Frames | количество кадров в анимации | 50 |
Generations | количество итераций L-системных правил | 5 |
IterationRules | правила итерации L-системы | |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет строк | RGB::Blue |
LineWidth | ширина строк | 0.35 |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость строк | TRUE |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
RotationAngle | угол команд вращения в L-системах | |
StartRule | запустите правило L-системы | |
StepLength | продолжительность команд перемещения в L-системах | 1.0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TurtleRules | правила, переводящие L-системные символы в перемещения черепахи | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Как очень простая система, мы рассматриваем следующее правило итерации: “замените каждую строку вперед последовательностью “строка вперед, продвиньтесь без рисования, строка вперед””.:
l := plot::Lsys(0, "F", "F" = "FfF"):
Обратите внимание на то, что мы не предоставляем правило итерации для "f". Это означает, “оставляют в покое f, не изменяйте его”.
Начальное состояние отображено путем графического вывода системы после нулевых поколений:
l::Generations := 0: plot(l)

Увеличивая число поколений, мы видим эффект нашего правила преобразования:
l::Generations := 1: plot(l)

l::Generations := 2: plot(l)

l::Generations := 3: plot(l)

Следующий вариант этого простого примера производит приближения для Канторова набора:
l := plot::Lsys(0, "F", "F" = "FfF", "f" = "fff"): plot(l)

Чтобы получить более интересные примеры, мы включаем вращения в наши правила:
l := plot::Lsys(PI/2, "F-F-F-F", "F" = "F-F+F+FF-F-F+F",
Generations = 3)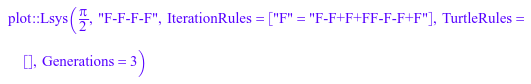
Как вы видите, plot::Lsys обнаружил, что наше правило является правилом итерации. Мы, возможно, использовали этот синтаксис непосредственно при создании объекта. Мы не дали правила черепахи, таким образом, значения по умолчанию используются:
plot(l)

Кривая Пеано является известным примером кривой заполнения пробела. В предельном процессе, увеличивая число итераций при уменьшении длины прямых шагов, это на самом деле заполняет плоскость. Существуют различные известные конструкции, один показанный здесь заполняет квадрат, наклоненный![]() :
:
peano := plot::Lsys(PI/2, "F", "F" = "F+F-F-F-F+F+F+F-F"):
Правило преобразования говорит, чтобы заменить каждую прямую линию на следующую конструкцию:
peano::Generations := 1: plot(peano)
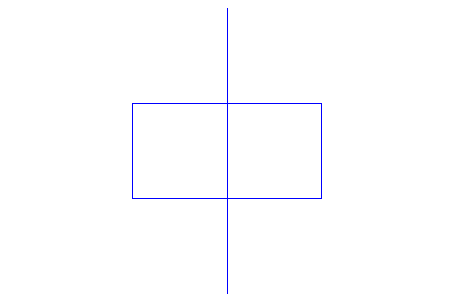
После нескольких итераций строки уже добираются очень друг близко к другу:
peano::Generations := 5: plot(peano)

Много L-систем содержат различные типы строк: В то время как они чертятся точно то же самое, их правила преобразования отличаются друг от друга. Следующий пример показывает изображение, подобное Треугольнику Серпинского:
l := plot::Lsys(PI/3, "R", "L" = "R+L+R", "R" = "L-R-L",
"L" = Line, "R" = Line,
Generations = 7):
plot(l)
Операции Push и Pop могут использоваться, чтобы чертить “руки” в L-системе:
plot(plot::Lsys(23*PI/180, "F", "F" = "FF-[-F+F+F]+[+F-F-F]",
Generations = 4))
L-системы использовались, чтобы моделировать рост объекта. Мы показываем пример здесь, который использует символы B, H и G, чтобы изменить цвет строк:
l := plot::Lsys(PI/9, "BL", "L" = "BR[+HL]BR[-GL]+HL",
"R" = "RR", "L" = Line, "R" = Line,
"B" = RGB::Brown, "H" = RGB::ForestGreen,
"G" = RGB::SpringGreen, Generations = 6):
plot(l)
Атрибут Generations может быть анимирован. Таким образом, мы можем на самом деле заставить “объект” “вырасти”:
plot(plot::Lsys(a*PI/45, "BL", "L" = "BR[+HL]BR[-GL]+HL", "R" = "RR",
"L" = Line, "R" = Line, "B" = RGB::Brown,
"H" = RGB::ForestGreen, "G" = RGB::SpringGreen,
Generations = a, a = 1 .. 6)):
L-системы могут отобразить несколько популярных фракталов. Одним примером является Снежинка Коха, сгенерированная, заменяя каждую прямую линию на прямую линию, сопровождаемую левым поворотом![]() , другую прямую линию, правый поворот
, другую прямую линию, правый поворот![]() , другую прямую линию, другой левый поворот
, другую прямую линию, другой левый поворот![]() и строку финишной прямой:
и строку финишной прямой:
koch := plot::Lsys(PI/3, "F--F--F", "F" = "F+F--F+F"):
Стартовое правило было выбрано, чтобы быть равносторонним треугольником:
koch::Generations := 0: plot(koch)

Первое поколение выглядит так:
koch::Generations := 1: plot(koch)

Предел вполне прилично аппроксимирован после пяти поколений:
koch::Generations := 5: plot(koch)

Наконец, мы используем plot::modify и слот "StepLength", чтобы показать эти первые две итерации, наложенные друг на друга:
colors := [RGB::Red, RGB::Green, RGB::Blue, RGB::Yellow, RGB::DimGrey]:
plot(plot::modify(koch, Generations = i,
StepLength = 3^(-i),
LineColor = colors[i+1]) $ i = 0..4)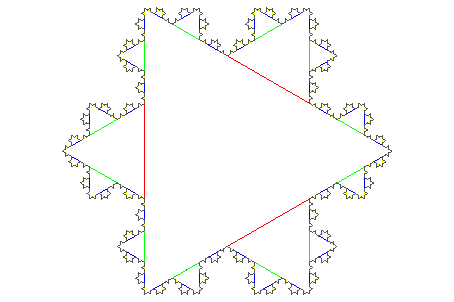
Другим известным примером фрактала, сгенерированного L-системой, является кривая Дракона Хивея. Неофициально, это сгенерировано путем “рисования прямого угла и затем заменяющий каждый прямой угол меньшим прямым углом” (Гарднер). Это использовалось в книге “Парк юрского периода” Майкла Крайтона и таким образом получило другой псевдоним, “фрактал Парка юрского периода”:
plot(plot::Lsys(PI/2, "L", "L" = "L+R+", "R" = "-L-R",
"L" = Line, "R" = Line, Generations = 9))
Интересно отметить, что правила итерации этой кривой эквивалентны добавлению зеркальной копии кривой к ее концу:
plot(plot::Lsys(PI/2, "L", "L" = "L+R+", "R" = "-L-R",
"L" = Line, "R" = Line, Generations = a,
a = 1..9))
В то время как L-система предыдущего примера соответствует определению, найденному в литературе, изображения по крайней мере в одном популярном источнике показывают другую систему (в то время как данным определением является то сверху), а именно:
plot(plot::Lsys(PI/4, "X-F-Y", "X" = "X+F+Y", "Y" = "X-F-Y",
"X" = Line, "Y" = Line, Generations = 9)):
L-система может содержать буквы, которые не предназначены, чтобы показать в итоговой диаграмме, таким образом, они формируют своего рода “маркеры” для последующего iteations. С этой целью можно использовать правило черепахи Noop:
plot(plot::Lsys(PI/12,
"X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X",
"X" = "[F+F+F+F[---X-Y]+++++F++++++++F-F-F-F]",
"Y" = "[F+F+F+F[---Y]+++++F++++++++F-F-F-F]",
"X" = Noop, "Y" = Noop,
Generations = 3))
plot(plot::Lsys(PI/2, "FB",
"A" = "FBFA+HFA+FB-FA", "B" = "FB+FA-FB-JFBFA",
"F" = "", "H" = "-", "J" = "+",
"A" = Noop, "B" = Noop, "H" = Noop, "J" = Noop))
Используя это правило, мы можем использовать следующую формулировку популярной Гильбертовой кривой из-за Кена Филипа:
plot(plot::Lsys(PI/2, "x", "x" = "-yF+xFx+Fy-", "y" = "+xF-yFy-Fx+",
"x" = Noop, "y" = Noop))
Чтобы анимировать процесс создания Гильбертовой кривой, мы настраиваем длину строк к текущему количеству шагов итерации:
plot(plot::Lsys(PI/2, "x", "x" = "-yF+xFx+Fy-", "y" = "+xF-yFy-Fx+",
"x" = Noop, "y" = Noop,
Generations = i, StepLength = 1/(2^i-1),
i = 1..6, Frames = 6))
В некоторых случаях системам будут нужны маленькие углы и длинные строки в порядке задать желаемые направления. Возьмите, например, следующую систему:
plot(plot::Lsys(7*PI/15, "F", "F"="F+F--F+F",
Generations=4))
Вращения к праву используют угол![]() , в то время как это налево (резкий скачок) является поворотом
, в то время как это налево (резкий скачок) является поворотом![]() . Это выглядело бы более естественным, однако, чтобы иметь черепаху запускаются направо, т.е. под углом
. Это выглядело бы более естественным, однако, чтобы иметь черепаху запускаются направо, т.е. под углом![]() . Поскольку никакое кратное
. Поскольку никакое кратное![]() не равно
не равно![]() 2 π по модулю, это требует, чтобы мы использовали меньший угол, настраивая наше правило итерации:
2 π по модулю, это требует, чтобы мы использовали меньший угол, настраивая наше правило итерации:
plot(plot::Lsys(7*PI/30,"+++++++++++++++F",
"F"="F++F----F++F", Generations=4))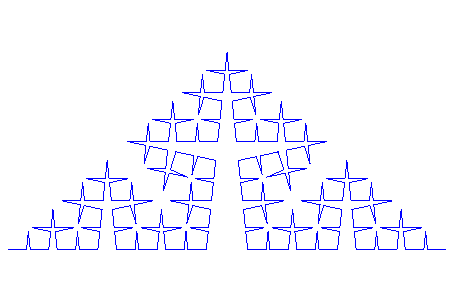
|
Угол (в радианах) для превращения команд. Animatable.
|
|
Строка используется в качестве стартового правила.
|
|
Итерация и правила команды Черепахи (см. ниже).
|
|
Параметр анимации, заданный как |
Системы Lindenmayer являются “системами перезаписи строки”. MuPAD® реализует только контекстно-свободные L-системы, которые анализируются в подобном контексте как бесконтекстные грамматики.
Много примеров L-систем могут быть найдены, среди других мест, во “Фрактальной Геометрии Природы” Бенуа Мандельбротом.