Описание

stats::gammaRandom(a, b) возвращает процедуру, которая производит гамму, отклоняет (случайные числа) с параметром формы a> 0 и масштабный коэффициент b> 0.

Процедура f:=stats::gammaRandom(a, b) может быть названа в форме f(). Возвращаемое значение f() является или числом с плавающей запятой или символьным выражением:

Если a и b могут быть преобразованы в положительные числа с плавающей запятой, то f() возвращает неотрицательное число с плавающей запятой.

Во всех других случаях stats::gammaRandom(a, b)() возвращен символически.

Численные значения a и b только приняты, если они действительны и положительны.

Значения X = f() распределяются случайным образом согласно кумулятивной функции распределения гамма распределения с параметрами a и b. Для любых 0 ≤ x, вероятность, что X ≤ x дают

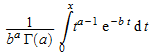Без опции Seed = n, начальный seed выбран внутренне. Этот начальный seed установлен в значение по умолчанию, когда MuPAD^® запускается. Таким образом, каждый раз, когда MuPAD запускается или повторно инициализируется с функцией reset, случайные генераторы производят те же последовательности чисел.

Для эффективности рекомендуется произвести последовательности случайных чисел K через

f := stats::gammaRandom(a, b): f() $k = 1..K;

вместо

stats::gammaRandom(a, b)() $k = 1..K;

Последний вызов производит последовательность генераторов, каждый из которых называется однажды. Также отметьте это

stats::gammaRandom(a, b, Seed = n)() $k = 1..K;

не производит случайную последовательность, потому что последовательность недавно инициализированных генераторов была бы создана каждый из них производящий тот же номер.

Обратите внимание на то, что.