статистика::Кумулятивная функция распределения логарифмически нормального распределения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
stats::lognormalCDF(m, v)
stats::lognormalCDF(m, v) возвращает процедуру, представляющую кумулятивную функцию распределения
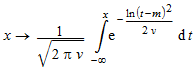
из логарифмически нормального распределения с параметром положения m и параметр формы v.
X случайной переменной логарифмически нормально распределяется, если ln (X) является нормально распределенной переменной. “Параметр положения” m X является средним значением ln (X) и “параметр формы” v, является отклонением ln (X).
Процедура f := stats::lognormalCDF(m, v) может быть названа в форме f(x) с арифметическим выражением x. Значение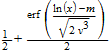
возвращено.
Если x является числом с плавающей запятой, и и m и v могут быть преобразованы в числа с плавающей запятой, это значение возвращено как число с плавающей запятой. В противном случае символьное выражение возвращено.
Численные значения для m и v только приняты, если они действительны, и v положителен.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы оцениваем CDF логарифмически нормального распределения для некоторых произвольных значений параметров:
f := stats::lognormalCDF(1/2, 3/4): f(0.1), f(10.3)
delete f:
Мы используем символьные аргументы:
f := stats::lognormalCDF(m, v): f(3), f(x)
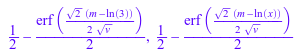
Когда численные значения присвоены m и v, функциональный f начинает производить численные значения:
m := 4: v := PI: f(3), f(3.0)
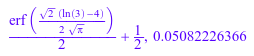
delete f, m, v:
Из определения “логарифмически нормальных” выше его ясно, что вероятность X <0 является нулем для X, логарифмически нормально распределенного:
plotfunc2d(stats::lognormalCDF(0,1))
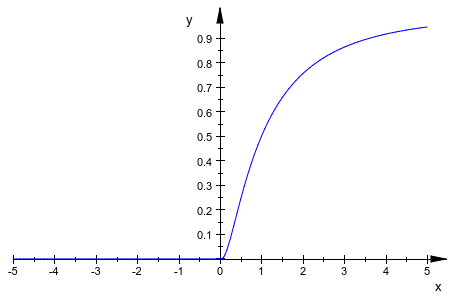
Следующий график показывает влияние параметра формы на форме логарифмически нормального распределения:
f03 := stats::lognormalCDF(0, 0.3): f1 := stats::lognormalCDF(0, 1): f3 := stats::lognormalCDF(0, 3): f9 := stats::lognormalCDF(0, 9): plotfunc2d(f03, f1, f3, f9, x = 0..10)
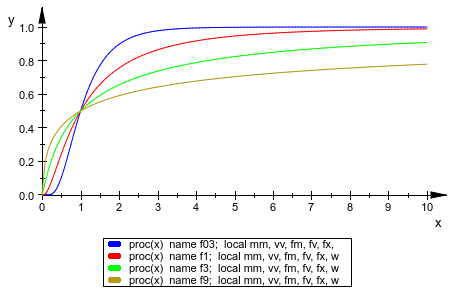
Что касается нормального распределения, большее значение параметра формы расширяет логарифмически нормальное распределение, также изменяя его форму в процессе:
plotfunc2d(stats::lognormalCDF(m, 1)$ m = 0..2 step .1,
LegendVisible = FALSE)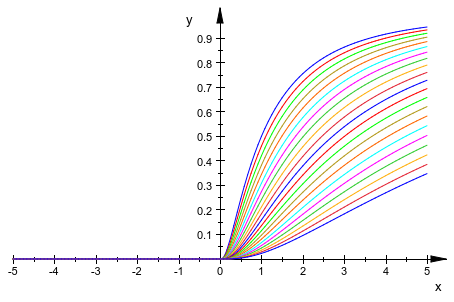
|
Параметр положения: арифметическое выражение, представляющее действительное значение |
|
Параметр формы: арифметическое выражение, представляющее положительное действительное значение |