Документация

Вычислите обобщенный ряд

Расширение Ряда Тейлора является наиболее распространенным способом аппроксимировать выражение полиномом. Однако не все выражения могут быть представлены Рядом Тейлора. Например, вы не можете вычислить расширение Ряда Тейлора для следующего выражения вокруг x = 2:

taylor(1/(x^3 - 8), x = 2)

Error: Unable to compute Taylor expansion of '1/(x^3 - 8)'. Try 'series' for a more general expansion. [taylor]

Если расширение Ряда Тейлора не существует для вашего выражения, попытайтесь вычислить другой степенной ряд. MuPAD^® обеспечивает функциональный series для ряда вычислительной мощности. Когда вы вызываете series, MuPAD пытается вычислить следующий степенной ряд:

Как только series вычисляет любой тип степенного ряда, это не продолжает вычислять другие типы ряда, но останавливает и возвращает результат. Например, для этого выражения это возвращает Ряд Лорана:

S := series(1/(x^3 - 8), x = 2);
testtype(S, Type::Series(Laurent))

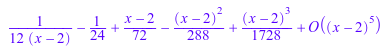
Когда вычислительные последовательные расширения, MuPAD возвращает только те результаты, которые допустимы для всех комплексных чисел переменной расширения в некотором окружении точки расширения. Если вам нужно расширение, чтобы быть допустимыми только для вещественных чисел, используйте опцию Real. Например, когда вы вычисляете последовательное расширение следующего выражения для комплексных чисел, series возвращается:

series(sign(x^2*sin(x)), x = 0)

Когда вы вычисляете последовательное расширение для вещественных чисел, series возвращает упрощенный результат:

series(sign(x^2*sin(x)), x = 0, Real)

Вдоль вещественной оси вычислите последовательные расширения для этого выражения, когда x приблизится к значению 0 слева и с правых сторон:

series(sign(x^2*sin(x)), x = 0, Left);
series(sign(x^2*sin(x)), x = 0, Right)