Документация

Упростите специальные функции автоматически

MuPAD^® обеспечивает много специальных функций, обычно используемых в разработке и науке. MuPAD использует стандартные математические обозначения для специальных функций. Если вы не распознаете обозначение, смотрите Математическое Использование Обозначений в Набранном Режиме.

Конкретный выбор параметра может упростить специальные функции. Часто MuPAD обрабатывает такие упрощения автоматически. Например, следующие параметры уменьшают гипергеометрические функции до элементарных функций:

hypergeom([], [], z);
hypergeom([1], [], z);
hypergeom([a], [], z)

Используйте генерала Симплифирса, чтобы уменьшать специальные функции

MuPAD автоматически не упрощает некоторые функции. Например, это автоматически не упрощает Майера Г специальная функция:

meijerG([[], []], [[1], []], z)

Общие функции упрощения, simplify и Simplify, представляют это выражение с точки зрения элементарных функций:

simplify(meijerG([[], []], [[1], []], z))

MuPAD также не использует автоматические упрощения для многих выражений, включающих специальные функции. Предположим, что вы получаете выражение, содержащее Функцию вычисления интеграла синуса Френеля:

2*fresnelS(z) + fresnelS(-z)

Чтобы применить отражательное правило fresnelS(-z) = -fresnelS(z) и упростить это выражение, явным образом вызовите один из общих simplifiers:

simplify(2*fresnelS(z) + fresnelS(-z))

Особые значения параметров могут уменьшать более общие специальные функции до выражений, содержащих более простые специальные функции. Например, уменьшайте meijerG до гипергеометрических функций:

Simplify(meijerG([[1/3, 1/3, 3/2], []], [[0], [-2/3, 4/3]], z))

Следующий выбор параметров выражает meijerG с точки зрения Функций Бесселя:

simplify(meijerG([[], []], [[1], [1]], z))

Расширьте выражения, включающие специальные функции

MuPAD поддерживает расширения выражений, содержащих специальные функции. Получившиеся выражения могут включить исходные или дополнительные специальные функции или обоих. Например, команда expand выражает бета-функцию гамма функциями:

beta(x + 1, y) = expand(beta(x + 1, y))

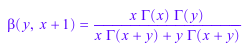
Когда вы расширяете гамма функцию, MuPAD выражает ее с точки зрения гамма функций:

gamma(5*x + 1) = expand(gamma(5*x + 1))

Проверьте решения, включающие специальные функции

При решении уравнений (особенно обыкновенные дифференциальные уравнения) вы часто получаете результаты с точки зрения специальных функций. Например, рассмотрите следующее дифференциальное уравнение:

eq := diff(y(x), x, x) - x^3*y(x) = 0

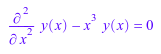
Для этого ОДУ решатель возвращает результат с точки зрения Функций Бесселя:

S := solve(ode(eq, y(x)))

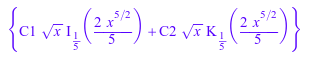
Чтобы проверить правильность возвращенного решения, попытайтесь заменить им в исходное уравнение при помощи evalAt или его ярлыка |. Вы получаете следующий длинный и сложный результат, который все еще содержит функцию Бесселя специальные функции. MuPAD автоматически не упрощает этот результат:

eq | y(x) = S[1]

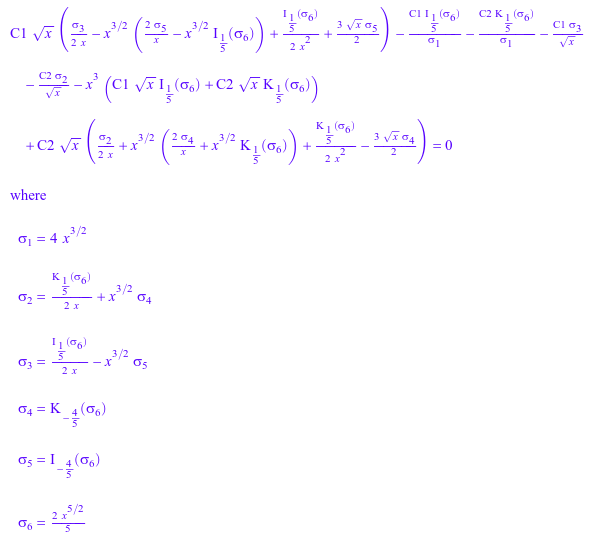
Упрощение этого выражения доказывает правильность решения:

simplify(eq | y(x) = S[1])

Команда testeq служит лучше всего для проверки правильности решений. Команда автоматически упрощает выражения с обеих сторон уравнения:

testeq(eq | y(x) = S[1])

Для получения дополнительной информации смотрите Результаты Тестирования.